This post is a translation of the article "Passage du Carré Magique au Tore Magique," first published in French on the 11th November 2011.
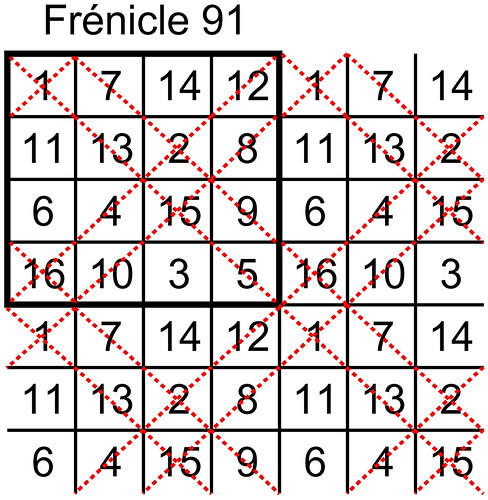
To visualise a magic torus let's begin with the Frénicle index square n° 91 (Bernard Frénicle de Bessy's classification of 880 fourth order magic squares - published posthumously in 1693 in his book "Des Quarrez Magiques" - see the listing on Harvey Heinz's site - Frénicle n°s 1 - 200, Frénicle n°s 201 - 400, Frénicle n°s 401 - 600, Frénicle n°s 601 - 880):
To visualise a magic torus let's begin with the Frénicle index square n° 91 (Bernard Frénicle de Bessy's classification of 880 fourth order magic squares - published posthumously in 1693 in his book "Des Quarrez Magiques" - see the listing on Harvey Heinz's site - Frénicle n°s 1 - 200, Frénicle n°s 201 - 400, Frénicle n°s 401 - 600, Frénicle n°s 601 - 880):
Extending this magic square we can construct a matrix of possibilities sized (2N-1)² to discover the other squares that are displayed on the magic torus:
This way we can find another 15 squares. We can see that there are 4 partially pandiagonal squares and 12 semi-magic squares displayed on the magic torus:
Then we can convert the squares that we have found into Frénicle standard form:
We can see that the magic torus displays not only the partially pandiagonal square Frénicle n°91, but also 3 other partially pandiagonal squares (Frénicle n°150, 320, and 394), as well as 12 semi-magic squares.
We are looking at the partially pandiagonal torus type n° T4.03.1.2. (index n° T4.174):
Ironically, although the procedure is invaluable in eliminating doubles, conversion into Frénicle standard form (by rotation, transposition, and / or reflection) has until today concealed the toroidal continuity of magic squares.
Ironically, although the procedure is invaluable in eliminating doubles, conversion into Frénicle standard form (by rotation, transposition, and / or reflection) has until today concealed the toroidal continuity of magic squares.
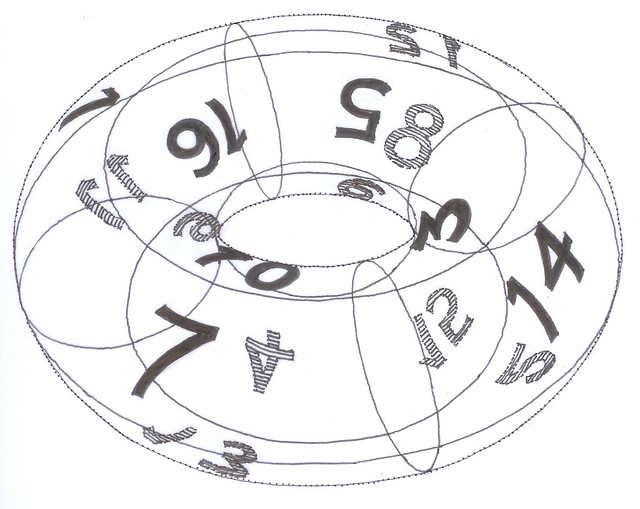
In the end, magic squares are to be observed in only two fundamental ways: either from outside the torus or from within, and it does not really matter which, as the torus can always be turned inside out...
 |
| Inside-out torus by Surot [Public domain], via Wikimedia Commons |




No comments:
Post a Comment
Or, should you prefer to send a private message, please email william.walkington@wandoo.fr