Si on passe sous silence
le carré magique d'ordre 1, le deuxième plus petit carré magique normal est de dimension 3 x 3 :
 |
| Ce carré magique est dans le domaine public |
Le carré magique de 3 x 3 est le seul en son genre si on ne compte pas ses sept frères obtenus par réflexion ou par rotation. On constate que la somme ou constante magique de chaque ligne, colonne, et des deux diagonales est de 15. La constante magique d’un carré est le ‘nombre triangulaire’ de sa dimension carrée divisée par sa dimension (l'ordre du carré magique):
Parfois appelé ‘Carré de Salomon’, le carré magique de 3 x 3 est réputé avoir figuré sur des documents écrits à l’époque des premiers empereurs Han - dont le début de la dynastie était 202 avant l’ère chrétienne.
Les carrés magiques, entourés de mystère depuis des siècles, se sont fait attribuer des pouvoirs spéciaux, et pour cette raison sont souvent représentes sur les jetons talismaniques qu’on trouve dans les grandes collections de médailles.
En 1533 le mage Henry Cornélius Agrippa consacrait le Livre Second de sa ‘Philosophie Occulte’ à la « magie céleste ». Le chapitre XXII traite ‘Des tables des planètes, de leurs vertus et formules, et quels sont les Noms divins, les Intelligences et les Daimons qui les gouvernent’.
« Les Mages, enseigne-t-il, nous ont transmis les sceaux et les Nombres des Sept Planètes, qu’on appelle aussi Tables Sacrées, car elles représentent l’harmonie des nombres célestes …Cette harmonie ne peut s’exprimer que par des chiffres et des charactères. Ces représentations matérielles des Nombres et des Signes ne sont rien d’autre dans le mystère des choses cachées que la figuration des Nombres essentiels qui dirigent et forment les choses à partir des Nombres Divins par l’intermédiaire des intelligences. » Les ‘tables planétaires’ qui illustrent le livre d’Agrippa ne sont autres que des carrés magiques. Agrippa a ainsi publié dans leur forme traditionnelle sept carrés magiques de dimension 3 x 3 à 9 x 9 et les a associés aux sept planètes:
 |
| Les carrés magiques d'Agrippa sont dans le domaine public |
L’ordre d’attribution planétaire des sept carrés magiques traditionnels semble être inspiré par la conception cosmographique de Ptolémée, elle-même dérivée du système géocentrique Pythagoricien. Ptolémée (astronome grec décédé à Alexandrie en l’année 168) affirmait que la Terre était au centre de l’univers et que les planètes y compris le Soleil tournaient autour d’elle en orbites sphériques concentriques. Dans l’ordre croissant de leurs distances à la Terre ces sphères étaient celles de la Lune, de Mercure, de Venus, du Soleil, de Mars, de Jupiter, et de Saturne, avec une huitième sphère pour les étoiles fixes. Le concept de Ptolémée était adopté par l’Eglise qui considérait que la terre était au centre de la création et que le paradis et l’enfer se trouvaient au-delà de la huitième sphère.
Défiant le Saint-Office, par leurs efforts (et parfois par leurs sacrifices), des hommes tels que Nicolas Copernic, Giordanno Bruno, Johannes Kepler et Galileo Galilei ont réussi à imposer le concept héliocentrique.
Aujourd’hui nous savons que les planètes y compris la Terre décrivent des orbites elliptiques autour du Soleil, lui-même une étoile moyenne au bord d’une des million million galaxies dans l’univers observable, et nous connaissons l’existence des planètes Uranus, et Neptune, mais faut-il pour autant remettre en question la valeur symbolique des tables planétaires décrites par Agrippa ?
Dans son livre ‘Les Carrés Magiques’ Lucien Gérardin indique que ce n’est qu’en 1940 que l’occultiste et magicien Robert Ambelain compléta la série des sept carrés traditionnels d’Agrippa avec une publication dans La Géomancie magique d’un carré de dimension Dix, qui serait celui de la Terre.
Au début du Livre Second de son ouvrage ‘La Philosophie Occulte’ Agrippa avait écrit : ‘Les sciences de la Mathématique sont si nécessaires à la Magie, et ont tant de liaison avec elle, que ceux qui se mêlent de l’une sans employer l’autre ne font rien qui vaille. Ils perdent leur temps et ne viennent jamais à bout de leur dessein. Tout ce qui existe et tout ce qui se fait ici-bas par l’opération des forces naturelles est conduit avec nombre, poids, mesure et harmonie.’
Il existe deux courants de recherche sur les carrés magiques, celui des mages et celui des mathématiciens aussi éminents que Pascal, Frénicle et Euler pour ne citer que ces quelques noms. Lucien Gérardin écrit que « Ces deux courants sont nullement opposés mais bien complémentaires. On mutilerait le sens profond des carrés magiques si on n’étudiait ces derniers d’un seul point de vue. On le mutilerait davantage si l’on réduisait sa curiosité aux sept carrés planétaires traditionnels, en passant ainsi à coté de l’immense richesse du domaine. »
En effet le nombre de carrés magiques normaux ne se limite pas aux exemples de carrés magiques traditionnels publiés par le mage Cornélius Agrippa : Si le carré 3 x 3 est unique, à partir du carré de dimension 4 x 4 le nombre de carrés magiques possibles augmente de façon exponentielle. Les carrés magiques de dimension 4 x 4 comptent déjà 880 membres, les carrés magiques de dimension 5 x 5 en comptent 275 305 224, et les nombres de solutions des plus grands carrés magiques approchent rapidement l'infini.
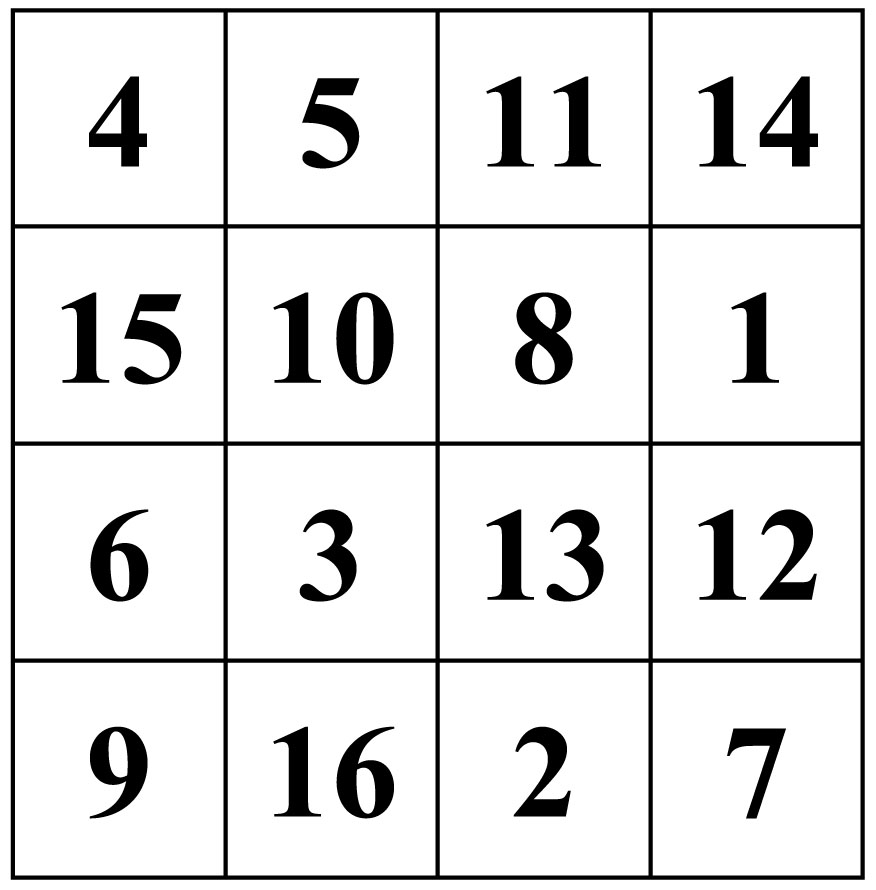
Le carré magique suivant de dimension quatre est un carré remarqué aux Indes par le révérend Frost, un missionnaire anglais qui évangélisait dans ce pays au XIXe siècle. Le carré ornait la grille de la porte d’entrée du vieux fort de Gwalior.
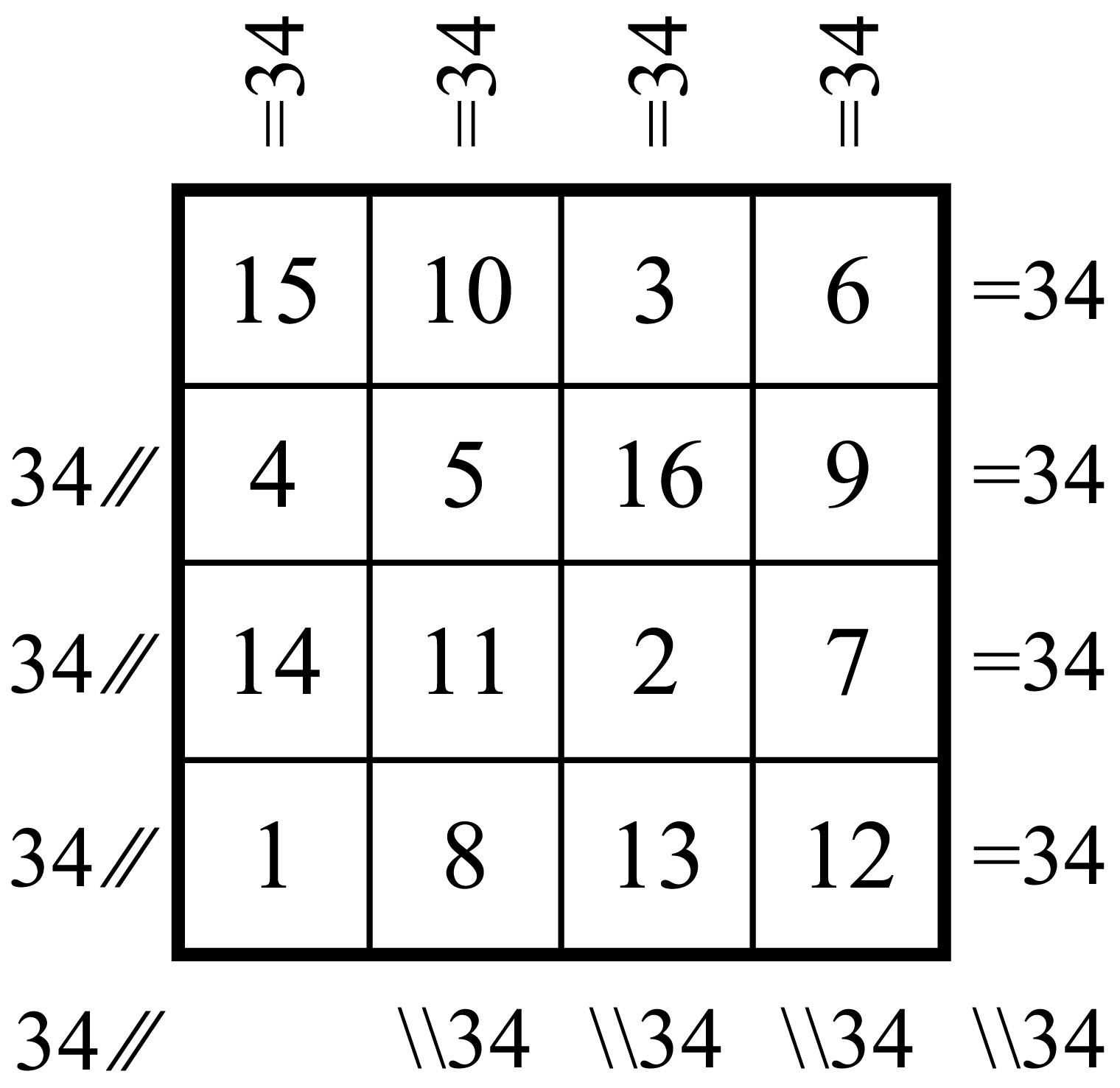 |
| Ce carré magic de Gwalior est dans le domaine public |
|
Il s’agit d’un carré dit
« diabolique », ou parfois panmagique, pandiagonal, continu, parfait, Nasik, ou Jaïna (la dernière appellation puisque le carré en question aurait été tracé par un savant Jaïna). Outre la magie selon les lignes, colonnes et diagonales principales, il y a aussi une magie selon toutes les diagonales brisées.
Il existe 48 carrés diaboliques de dimension 4 x 4, et 3 600 carrés diaboliques de dimension 5 x 5. Par contre aucun des carrés magiques normaux de dimension impairement paire (le 6 x 6 par exemple) n’est diabolique !
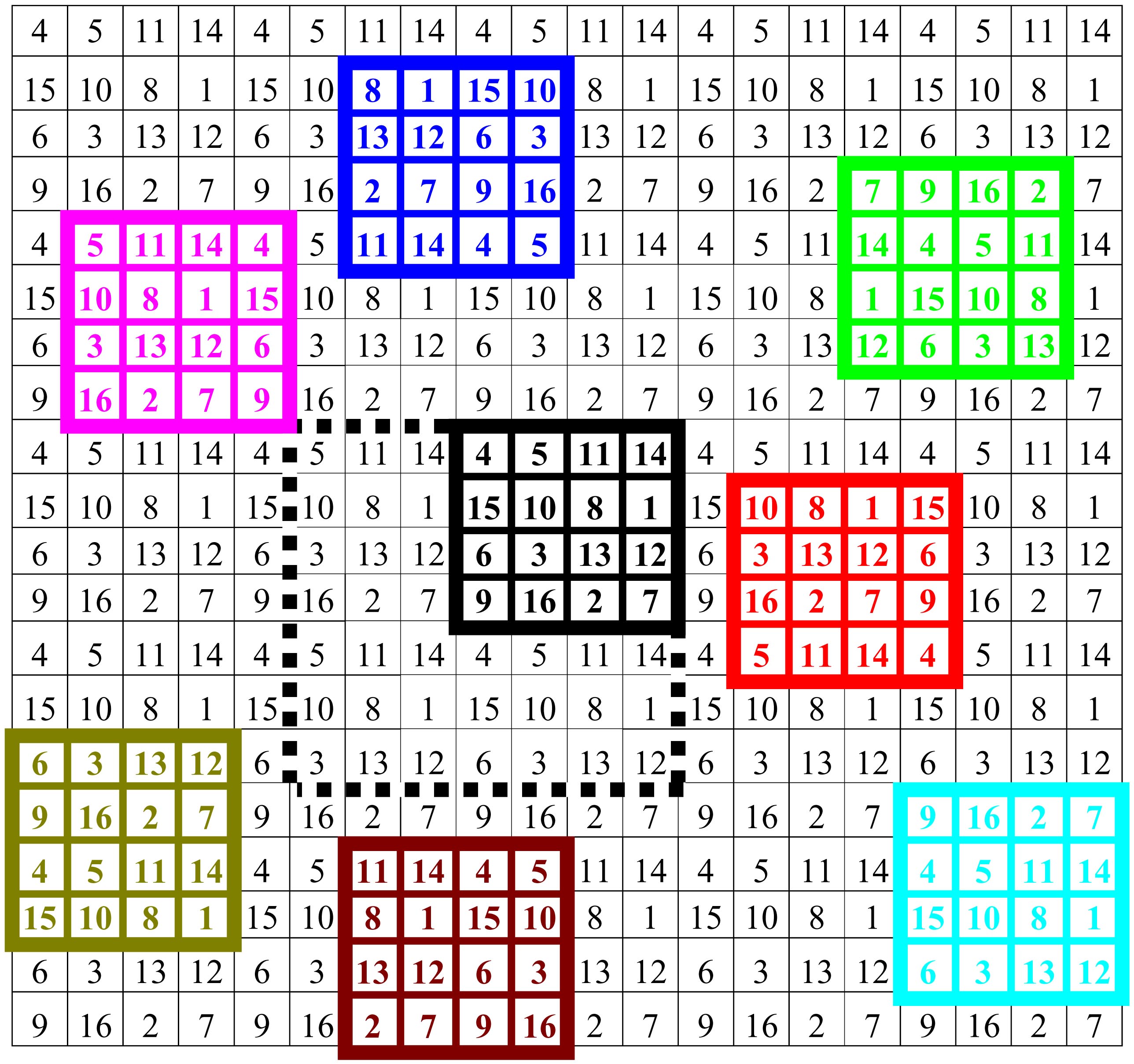
En prolongeant à répétition des lignes, colonnes et diagonales d’un carré diabolique on obtient un tableau de nombres qui s’enchaînent à l’infini. Sur ce quadrillage, à partir du carré diabolique de base (ici coloré noir) il est possible de générer plusieurs autres carrés différents qui possèdent tous des propriétés panmagiques:
Tous les carrés diaboliques formés ainsi peuvent exister dans une zone de sept fois sept cases (ici indiquée par l’enceinte pointillée) au-delà de laquelle les carrés deviennent redondants à cause d’un phénomène de bouclage. Partant d’un carré diabolique de dimension N fois N le nombre de carrés différents qui existent dans le système est de N². Dans l’exemple illustré 16 carrés diaboliques différents existent dans le système mais s’agit-il plutôt de 16 différents points de vue d’un même carré ?