Les Carrés Magiques et les Sphères - 3

Le carré magique et la sphère sont associés dans la gravure sur cuivre d’Albrecht Dürer « Melencolia I » datée de 1514. « Melencolia I » est un œuvre symbolique majeur qui fait l’objet d’interprétations multiples. Les symboles illustrés dans cette allégorie semblent décrire des connaissances qui sont perdues, ou des défis qui dépassent le commun des mortels – tels que le problématique impossible de la quadrature du cercle. On peut y trouver un carré magique, un polyèdre, et une sphère.

Albrecht Dürer's Melencolia I [Public domain], via Wikimedia Commons

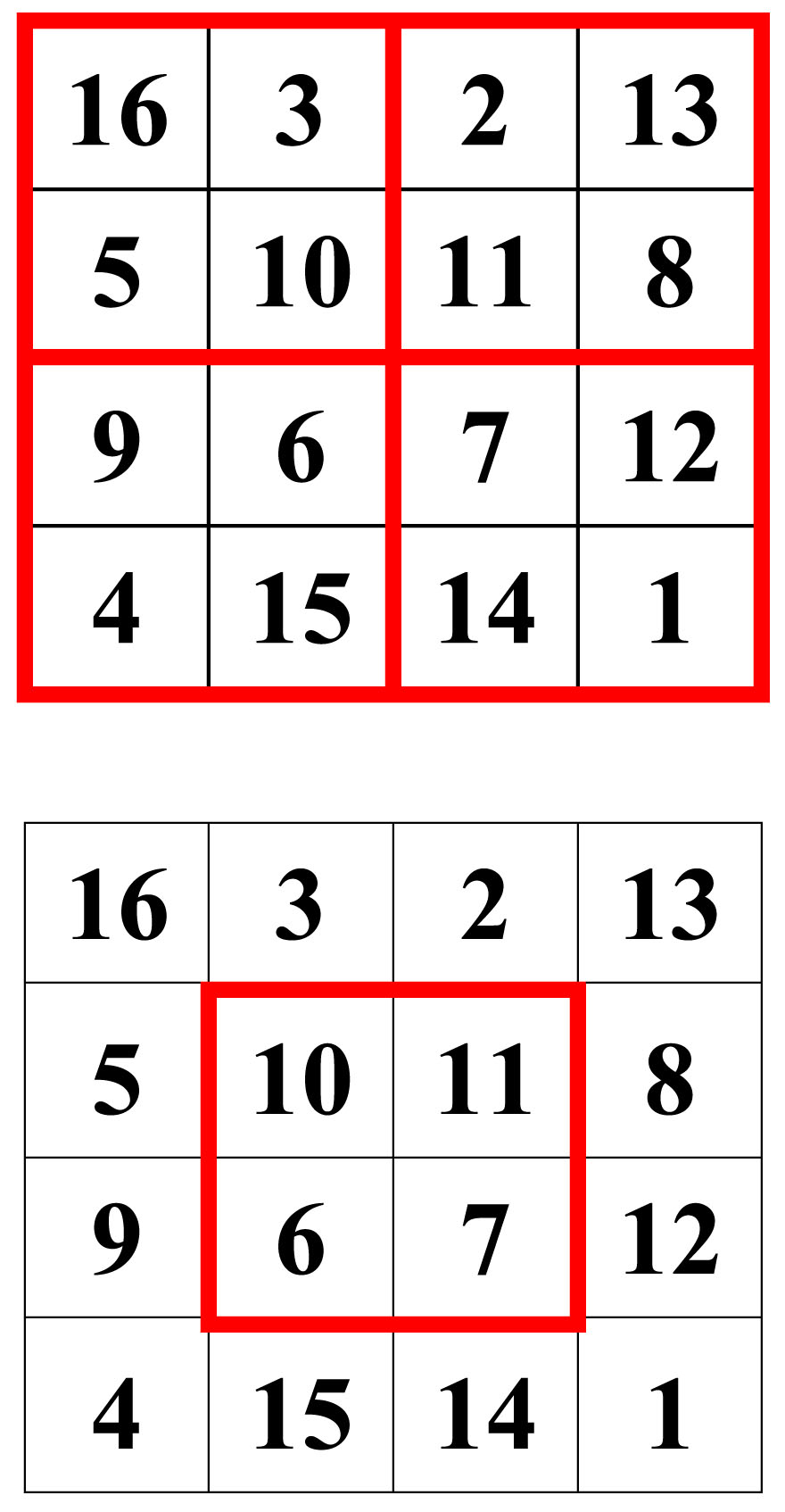
Le carré de Dürer n’est pas panmagique mais il a la particularité d’être gnomon : En plus des caractéristiques d’un carré magique classique ayant un constat magique de 34, les sommes de chacun de ces quatre quadrants ainsi que la somme des nombres du carré du milieu sont toujours de 34. 3 et 4 sont significatifs car ils apparaissent en symétrie dans la Tetrakys Pythagoricienne : 1+2+3+4 = 10 = 3+4+3.

Le polyèdre est d’une construction originale qu’on appelle « polyèdre de Dürer ». Ce polyèdre de 8 faces est sphérique, ayant tous ses sommets situés à égale distance par rapport à un centre. Dans « A new hypothesis on Dürer’s enigmatic polyhedron in his copper engraving ‘Melencholia I’ » publié en 1999, P. Schreiber fait remarquer que ce solide peut être obtenu à partir d’un cube. Ce polyèdre sphérique contient donc le secret du passage du cube à la sphère. Le rapport entre le polyèdre et le carré magique est frappant car il y a une correspondance des faces projetées du solide et le carré arithmétique – voir l’illustration et la description qui proviennent de Wikimedia Commons:

Dürer's solid by Ael 2 [Public domain], via Wikimedia Commons

La sphère et le carré magique se trouvent dans deux angles diamétralement opposés sur un axe de composition de la gravure.

Est-ce que Dürer voulait mettre en exergue une relation particulière entre le carré magique, le polyèdre, et la sphère ? Le carré magique semble être la clé d’un énigme pythagoricienne – visible au spectateur mais négligé par le penseur, ou la penseuse, Melencolia.

En 2014, soit 500 ans après 1514, la date de création de Melencolia I, une nouvelle page est consacrée à cet anniversaire. Il s'agit de l'édition de carrés magiques commémoratives.

 

Aussi en 2014, Günter M. Ziegler a écrit un article très intéressant intitulé "Dürer's polyhedron: 5 theories that explain Melencolia's crazy cube." Cet article, publié dans la rubrique d'Alex Bellos, "Adventures in Numberland," est paru dans The Guardian le 3 décembre 2014.

Read more ...

Les Carrés Magiques et les Sphères - 2

On peut considérer que l’axe et la surface de la sphère magique soient libres et que les différentes lectures possibles de carrés magiques correspondent non seulement aux rotations des latitudes et des longitudes, mais aussi aux rotations de l’axe de la sphère par incréments de 90°. La lecture des carrés magiques étant possible depuis l'extérieur ou depuis l'intérieur de la sphère, tous les carrés obtenus par simple rotation ou simple réflexion peuvent être considérés comme carrés issus d'une même sphère magique.

L’exemple d’un carré « diabolique » ou panmagique est spectaculaire car la « magie » est présente dans toutes les directions. Mais dans le cas d’un carré magique normal, la lecture de la sphère donne des carrés qui ne sont pas toujours magiques sur leurs diagonales principales. Est-ce que ces derniers carrés sont moins magiques que leurs frères ou sœurs avec qui ils cohabitent sur la même sphère ?

On voit que la définition traditionnelle d’un carré magique est perturbée par le concept de sphère magique. Les nouvelles questions qui se posent sont :

1/ Si la définition traditionnelle d’un carré magique n'est plus valable, comment faut-il la redéfinir ?

2/ Supposant que chaque carré magique signifie la présence d’une sphère magique, mais n’exclue pas qu’autres carrés magiques existent sur la même sphère, il y a combien de différentes sphères magiques pour les carrés d’ordre 3x3 (1 seule sphère), 4x4, 5x5, 6x6 etc. ? Est-ce que le nombre de sphères magiques déduit par ordre de carré magique correspond à une suite mathématique connue ?

3/ Est-ce que les carrés magiques à enceinte sont groupés sur certaines sphères ?

N’ayant pas le temps et les moyens de calcul je ne sais pas répondre à ces questions et je préfère laisser le débat ouvert. Merci à l’avance pour vos contributions !

Read more ...