This post is a translation of the article "255 Tores Magiques d'Ordre 4, et 1 Tore Magique d'Ordre 3," first published in French on the 28th October 2011.
By rolling a square and then connecting the two ends of the cylinder, the limited surface of the square is transformed into the limitless surface of a torus. The torus permits a better visualisation of the scrolling numbers of a magic square, but with the inconvenient that certain numbers are hidden on the rear external surface and inside the ring.
 |
| "Torus from rectangle" by Lucas Vieira [Public domain], via Wikimedia Commons |
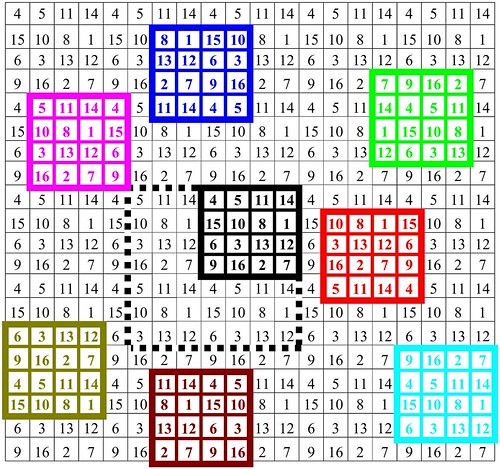
In order to optimise the visualisation of the scrolling effect we can take a new flattened look. When extending a repetition of the lines, columns and diagonals of a pandiagonal magic square we obtain a grid of numbers. On this grid, starting from the initial pandiagonal square (coloured black) it is possible to generate several other different squares that are all pandiagonal:
All the pandiagonal squares that are created this way can exist in a zone of seven by seven squares, (here indicated by the dotted enclosure), beyond which the squares become redundant because of the scrolling phenomenon. Beginning with an N-order pandiagonal square the number of different squares that exist in the system is N².
Convinced by the interest of this approach I chose to study the « Table générale des quarrez magiques de quatre » established by Bernard Frénicle de Bessy and published posthumously in 1693 in his book « Des quarrez magiques ». The census of these 880 4x4 squares is given in the appendix to the book « New Recreations With Magic Squares » by William H. Benson and Oswald Jacoby (Edition 1976) and also on the website of the late Harvey D. Heinz: Frénicle n° 1 à 200, Frénicle n° 201 à 400, Frénicle n° 401 à 600, Frénicle n° 601 à 880.
Thanks to the computing skills of Walter Trump the amended and extended results of this research now reveal the existence of 255 fourth-order magic tori and 4 038 fourth-order semi-magic tori:
Fourth-order Magic Tori
Fourth-order Magic Tori
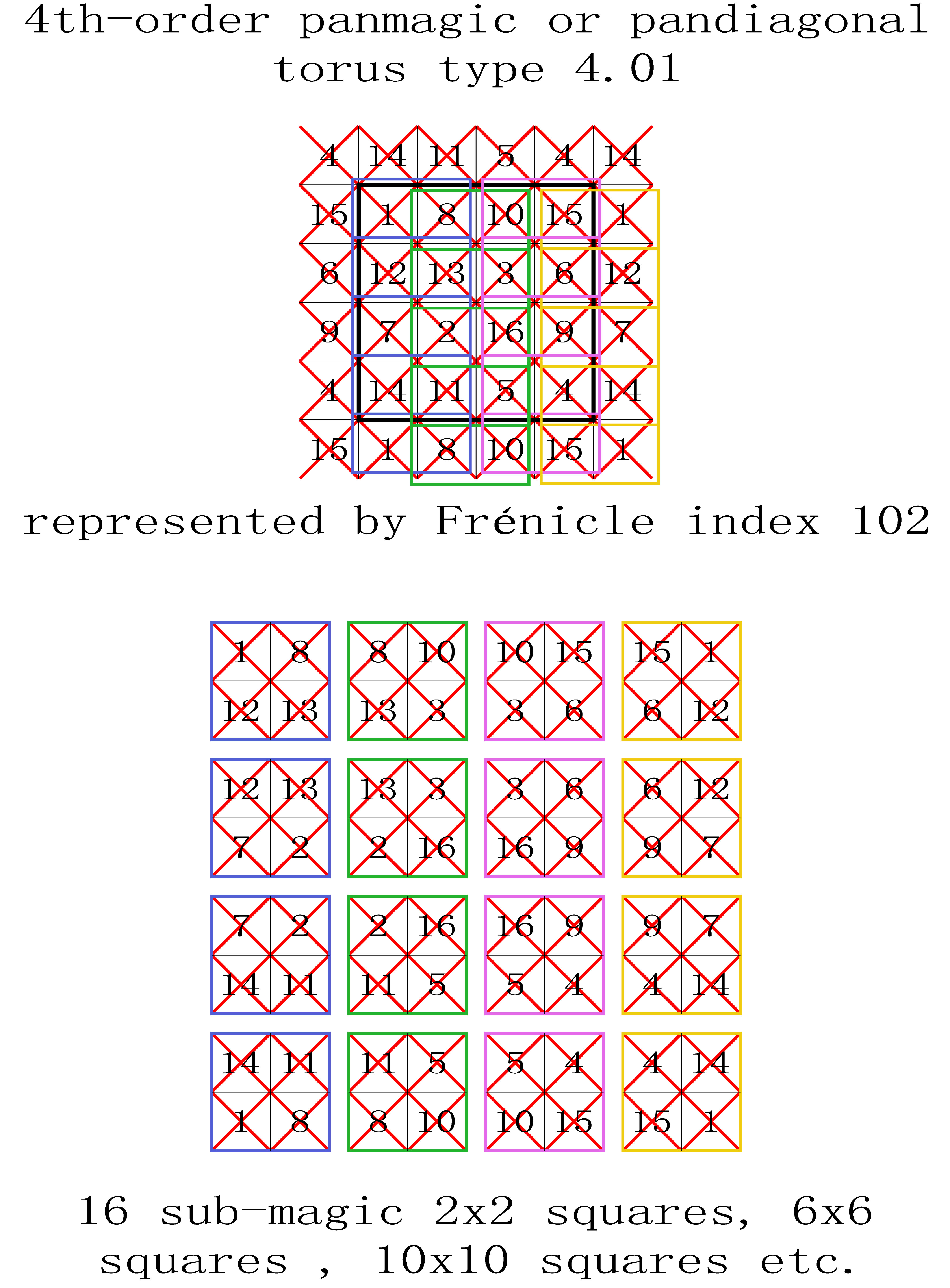
T4.01 Pandiagonal or Panmagic Tori Type 1
with 8 crossed magic diagonals producing 16 magic intersections.
Each torus type 1 is entirely covered by 16 sub-magic 2x2 squares.
All of the displayed pandiagonal squares are Dudeney type I.
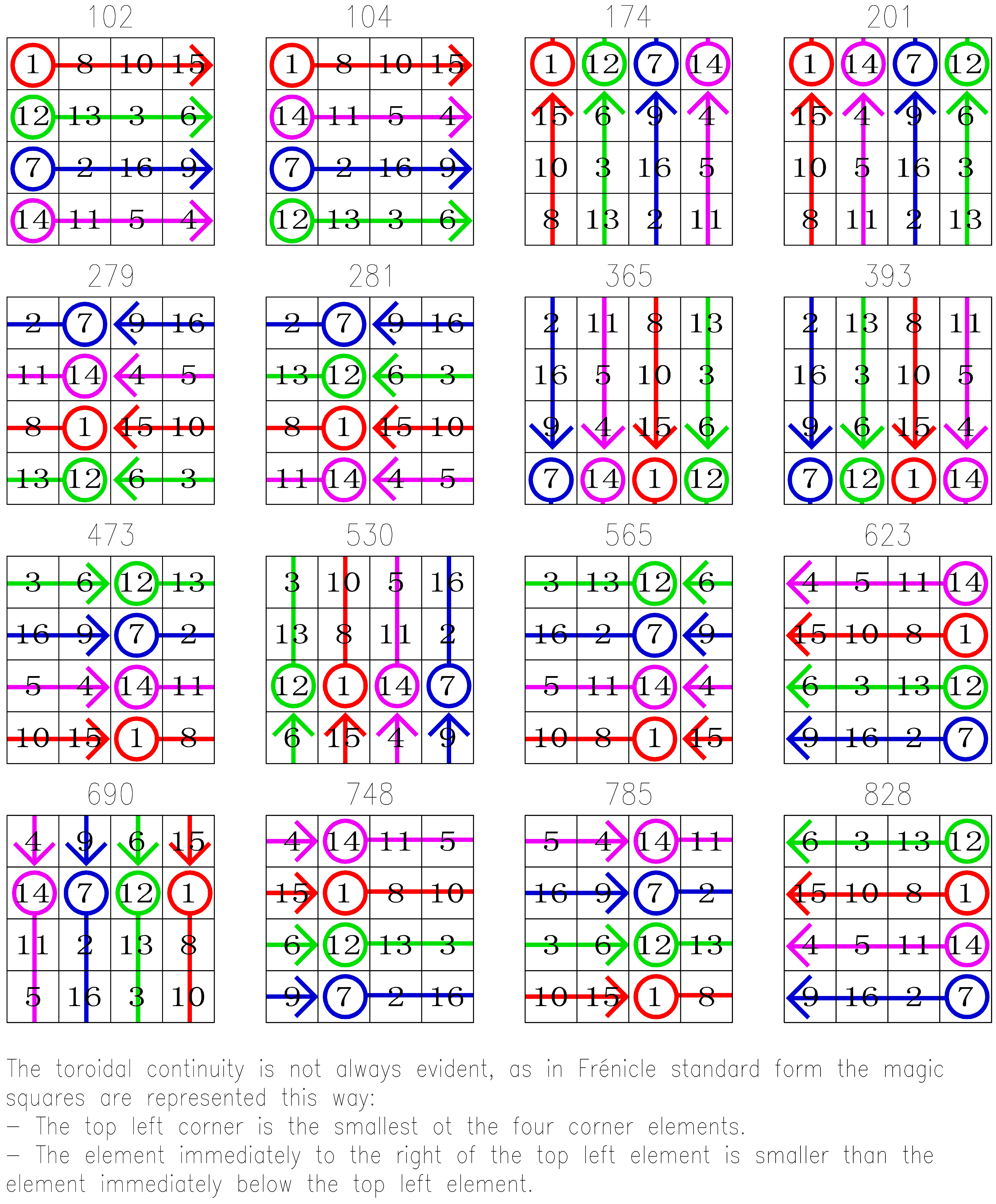
T4.01.1 (index n° T4.194):
16 pandiagonal squares Frénicle N°102, 104, 174, 201, 279, 281, 365, 393, 473, 530, 565, 623, 690, 748, 785 and 828. The torus is entirely covered by 16 sub-magic 2x2 squares.
For more details of how to find a magic torus, please refer to the article "From the Magic Square to the Magic Torus". Also, the "Table of Fourth-Order Magic Tori" shows how to convert any fourth-order magic square to normalised torus form, and thus discover the index number and complete details of the corresponding magic torus.
T4.01.2 (index n° T4.198):
16 pandiagonal squares Frénicle N°107, 109, 171, 204, 292, 294, 355, 396, 469, 532, 560, 621, 691, 744, 788, and 839. The torus is entirely covered by 16 sub-magic 2x2 squares.
T4.01.3 (index n° T4.213):
16 pandiagonal squares Frénicle N°116, 117, 177, 178, 304, 305, 372, 375, 483, 485, 536, 537, 646, 647, 702 and 704. The torus is entirely covered by 16 sub-magic 2x2 squares.
Total : 3 pandiagonal or panmagic tori type 1 that display 48 pandiagonal or panmagic squares, and 48 sub-magic 2x2 squares.
All of the displayed pandiagonal squares are Dudeney type I.
T4.02 Semi-pandiagonal Tori Type 2
with 4 crossed magic diagonals producing 8 magic intersections.
Each torus type 2.1 is entirely covered by 12 sub-magic 2x2 squares
Each torus type 2.2 is entirely covered by 8 sub-magic 2x2 squares
Each torus type 2.3 is entirely covered by 8 sub-magic 2x2 squares
T4.02.1 Semi-pandiagonal Tori Type 2.1
with 4 crossed magic diagonals producing 8 magic intersections.
Each torus type 2.1 is entirely covered by 12 sub-magic 2x2 squares.
Half of the displayed semi-pandiagonal squares are Dudeney type IV and the other half are Dudeney type VI.
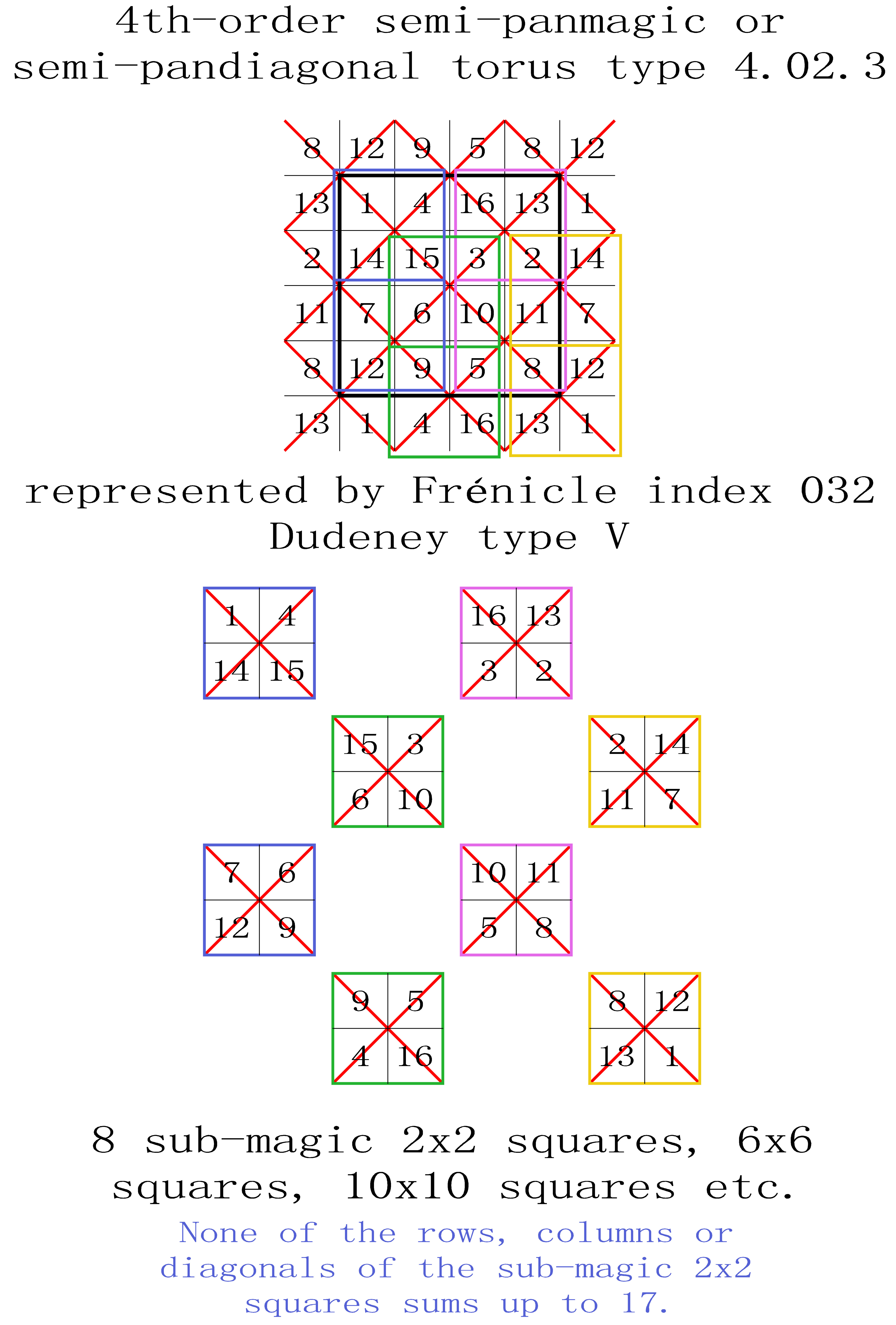
T4.02.1.01 (index n° T4.038):
8 semi-pandiagonal squares Frénicle N° 16, 160, 224, 385, 435, 603, 810, and 855, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.02 (index n° T4.027):
8 semi-pandiagonal squares Frénicle N° 17, 85, 225, 322, 436, 604, 778, and 843, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.03 (index n° T4.036):
8 semi-pandiagonal squares Frénicle N° 18, 141, 226, 334, 432, 599, 809, and 854, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.04 (index n° T4.023):
8 semi-pandiagonal squares Frénicle N° 19, 61, 227, 251, 433, 600, 766, and 817, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.05 (index n° T4.053):
8 semi-pandiagonal squares Frénicle N° 24, 137, 216, 342 443, 589, 806, and 859, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.06 (index n° T4.044):
8 semi-pandiagonal squares Frénicle N° 25, 55, 217, 262, 444, 590, 761, and 822, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.07 (index n° T4.073):
8 semi-pandiagonal squares Frénicle N° 30, 155, 236, 380, 419, 581, 802, and 851, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.08 (index n° T4.064):
8 semi-pandiagonal squares Frénicle N° 31, 77, 237, 313, 420, 582, 771, and 840, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.09 (index n° T4.115):
8 semi-pandiagonal squares Frénicle N° 48, 192, 255, 400, 570, 734, 763, and 824, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.10 (index n° T4.101):
8 semi-pandiagonal squares Frénicle N° 49, 93, 256, 326, 467, 498, 664, and 670, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.11 (index n° T4.111):
8 semi-pandiagonal squares Frénicle N° 54, 140, 261, 333, 499, 548, 671, and 715, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.12 (index n° T4.125):
8 semi-pandiagonal squares Frénicle N° 60, 136, 250, 341, 504, 543, 669, and 716, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.13 (index n° T4.138):
8 semi-pandiagonal squares Frénicle N° 64, 184, 273, 378, 507, 534, 681, and 696, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.14 (index n° T4.130):
8 semi-pandiagonal squares Frénicle N° 65, 74, 274, 311, 456, 508, 651, and 682, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.15 (index n° T4.155):
8 semi-pandiagonal squares Frénicle N° 73, 191, 310, 399, 572, 735, 774, and 842, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.16 (index n° T4.151):
8 semi-pandiagonal squares Frénicle N° 76, 159, 312, 384, 459, 515, 654, and 705, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.17 (index n° T4.165):
8 semi-pandiagonal squares Frénicle N° 84, 154, 321, 379, 451, 521, 649, and 708, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.18 (index n° T4.175):
8 semi-pandiagonal squares Frénicle N° 92, 182, 325, 367, 466, 540, 663, and 699, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.19 (index n° T4.201):
8 semi-pandiagonal squares Frénicle N° 110, 196, 287, 402, 566, 730, 791, and 836, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.20 (index n° T4.204):
8 semi-pandiagonal squares Frénicle N° 111, 195, 288, 401, 569, 731, 792, and 837, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.21 (index n° T4.220):
8 semi-pandiagonal squares Frénicle N° 119, 163, 296, 387, 488, 528, 636, and 713, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.22 (index n° T4.224):
8 semi-pandiagonal squares Frénicle N° 121, 162, 298, 386, 490, 527, 638, and 712, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.23 (index n° T4.226):
8 semi-pandiagonal squares Frénicle N° 123, 147, 307, 351, 475, 550, 630, and 723, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
T4.02.1.24 (index n° T4.231):
8 semi-pandiagonal squares Frénicle N° 125, 146, 309, 350, 477, 549, 633, and 722, and also 8 semi-magic squares. The torus is entirely covered by 12 sub-magic 2x2 squares.
Total : 24 semi-pandiagonal tori type 2.1 that display 192 semi-pandiagonal squares, 192 semi-magic squares, and 288 sub-magic 2x2 squares
Half of the displayed semi-pandiagonal squares are Dudeney type IV and the other half are Dudeney type VI.
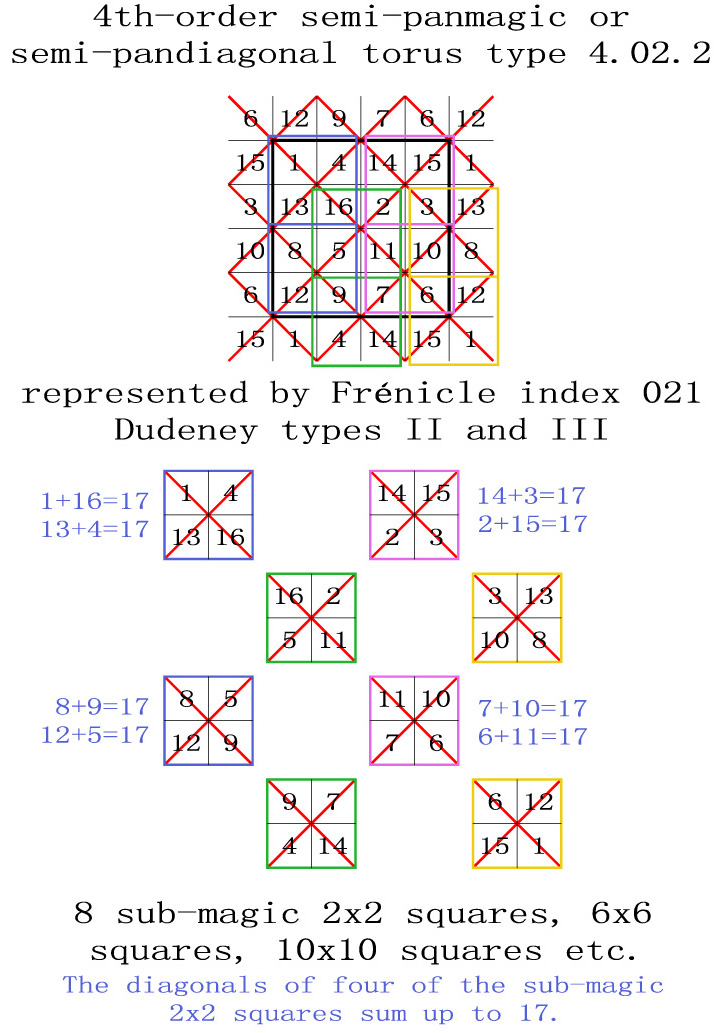
T4.02.2 Semi-pandiagonal Tori Type 2.2
with 4 crossed magic diagonals producing 8 magic intersections.Each torus type 2.2 is entirely covered by 8 sub-magic 2x2 squares.
Half of the displayed semi-pandiagonal squares are Dudeney type II and the other half are Dudeney type III (associated or self-complementary squares).
8 semi-pandiagonal squares Frénicle N° 21, 176, 213, 361, 445, 591, 808, and 860, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.2.02 (index n° T4.048):
8 semi-pandiagonal squares Frénicle N° 22, 113, 214, 290, 446, 592, 790, and 835, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.2.03 (index n° T4.077):
8 semi-pandiagonal squares Frénicle N° 27, 175 (the Dürer square), 233, 360, 421, 583, 803, and 850, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.2.04 (index n° T4.067):
8 semi-pandiagonal squares Frénicle N° 28, 112, 234, 289, 422, 584, 789, and 834, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.2.05 (index n° T4.127):
8 semi-pandiagonal squares Frénicle N° 56, 203, 246, 392, 562, 746, 768, and 818, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.2.06 (index n° T4.121):
8 semi-pandiagonal squares Frénicle N° 57, 122, 247, 299, 489, 503, 637, and 668, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.2.07 (index n° T4.137):
8 semi-pandiagonal squares Frénicle N° 62, 185, 269, 377, 505, 535, 678, and 695, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.2.08 (index n° T4.133):
8 semi-pandiagonal squares Frénicle N° 63, 120, 270, 297, 487, 506, 635, and 679, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.2.09 (index n° T4.164):
8 semi-pandiagonal squares Frénicle N° 82, 206, 316, 395, 558, 741, 779, and 844, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.2.10 (index n° T4.158):
8 semi-pandiagonal squares Frénicle N° 83, 126, 308, 317, 450, 478, 632, and 648, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.2.11 (index n° T4.173):
8 semi-pandiagonal squares Frénicle N° 89, 183, 323, 368, 464, 539, 661, and 698, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.2.12 (index n° T4.169):
8 semi-pandiagonal squares Frénicle N° 90, 124, 306, 324, 465, 476, 628, and 662, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
Total : 12 semi-pandiagonal tori type 2.2 that display 96 semi-pandiagonal squares, 96 semi-magic squares, and 96 sub-magic 2x2 squares.
Half of the displayed semi-pandiagonal squares are Dudeney type II and the other half are Dudeney type III (associated or self-complementary squares).
T4.02.3 Semi-pandiagonal Tori Type 2.3
with 4 crossed magic diagonals producing 8 magic intersections.
Each torus type 2.3 is entirely covered by 8 sub-magic 2x2 squares.
All of the displayed semi-pandiagonal squares are Dudeney type V.
T4.02.3.01 (index n° T4.085):
8 semi-pandiagonal squares Frénicle N° 32, 173, 228, 362, 425, 577, 798, and 853, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.3.02 (index n° T4.080):
8 semi-pandiagonal squares Frénicle N° 33, 108, 229, 293, 426, 578, 787,and 838, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.3.03 (index n° T4.084):
8 semi-pandiagonal squares Frénicle N° 34, 169, 230, 356, 423, 575, 797, and 852, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.3.04 (index n° T4.079):
8 semi-pandiagonal squares Frénicle N° 35, 103, 231, 282, 424, 576, 784, and 827, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.3.05 (index n° T4.145):
8 semi-pandiagonal squares Frénicle N° 66, 165, 264, 389, 511, 524, 674, and 710, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.3.06 (index n° T4.144):
8 semi-pandiagonal squares Frénicle N° 67, 115, 265, 302, 479, 512, 640, and 675, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.3.07 (index n° T4.146):
8 semi-pandiagonal squares Frénicle N° 68, 164, 266, 388, 513, 523, 676, and 709, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.3.08 (index n° T4.143):
8 semi-pandiagonal squares Frénicle N° 69, 101, 267, 280, 471, 514, 622, and 677, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.3.09 (index n° T4.183):
8 semi-pandiagonal squares Frénicle N° 95, 149, 328, 345, 460, 554, 657, and 721, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.3.10 (index n° T4.181):
8 semi-pandiagonal squares Frénicle N° 96, 114, 301, 329, 461, 481, 642, and 658, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.3.11 (index n° T4.184):
8 semi-pandiagonal squares Frénicle N° 97, 148, 330, 344, 462, 553, 659, and 720, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.02.3.12 (index n° T4.178):
8 semi-pandiagonal squares Frénicle N° 98, 106, 291, 331, 463, 468, 620, and 660, and also 8 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
Total : 12 semi-pandiagonal tori type 2.3 that display 96 semi-pandiagonal squares, 96 semi-magic squares, and 96 sub-magic 2x2 squares.
All of the displayed semi-pandiagonal squares are Dudeney type V.
T4.03 Partially pandiagonal Tori Type 3
with 4 crossed magic diagonals producing 4 magic intersections and 4 non magic intersections
Each torus type 3 is entirely covered by 8 sub-magic 2x2 squares.
Each torus type 3.1 displays partially pandiagonal squares Dudeney type VI.
Each torus type 3.2 displays partially pandiagonal squares Dudeney types VII and IX.
Each torus type 3.3 displays partially pandiagonal squares Dudeney type XI.
T4.03.1 Partially pandiagonal Tori Type 3.1
with 4 crossed magic diagonals producing 4 magic intersections and 4 non magic intersections.
Each torus type 3.1 is entirely covered by 8 sub-magic 2x2 squares.
All of the displayed partially pandiagonal squares are Dudeney type VI.
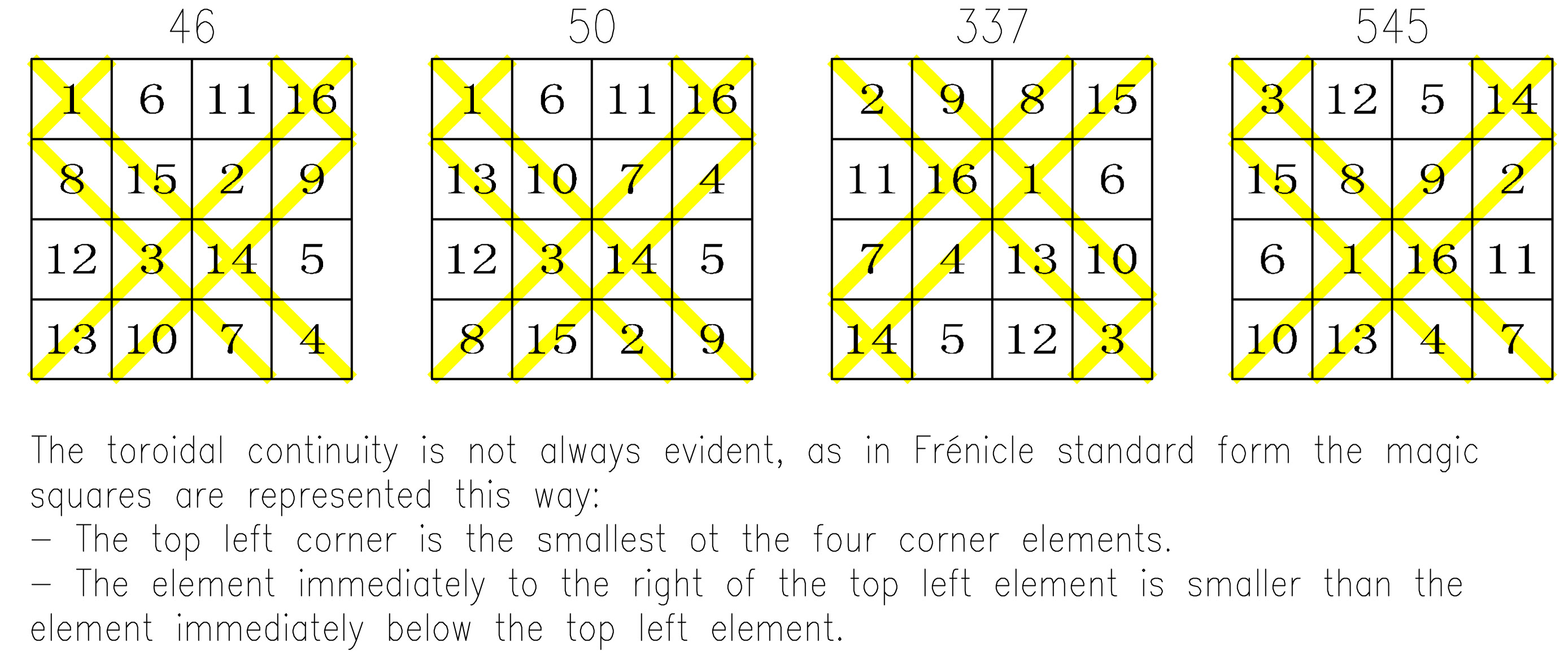
T4.03.1.1 (index n° T4.108):
4 partially pandiagonal squares Frénicle N° 46, 50, 337 and 545, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.1.2 (index n° T4.174):
4 partially pandiagonal squares Frénicle N° 91, 150, 320 and 394, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares. (see this torus here).
T4.03.1.3 (index n° T4.186):
4 partially pandiagonal squares Frénicle N° 100, 285, 617 and 793, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.1.4 (index n° T4.246):
4 partially pandiagonal squares Frénicle N° 132, 253, 259 and 719, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.1.5 (index n° T4.216):
4 partially pandiagonal squares Frénicle N° 179, 376, 482 and 645, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.1.6 (index n° T4.168):
4 partially pandiagonal squares Frénicle N° 187, 366, 667 and 780, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
4 partially pandiagonal squares Frénicle N° 187, 366, 667 and 780, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
Total : 6 partially pandiagonal tori type 3.1 that display 24 partially pandiagonal squares, 72 semi-magic squares, and 48 sub-magic 2x2 squares.
All of the displayed partially pandiagonal squares are Dudeney type VI.
T4.03.2 Partially pandiagonal Tori Type 3.2
with 4 crossed magic diagonals producing 4 magic intersections and 4 non magic intersections.
Each torus type 3.2 is entirely covered by 8 sub-magic 2x2 squares.
Half of the displayed partially pandiagonal squares are Dudeney type VII and the other half are Dudeney type IX.
T4.03.2.01 (index n° T4.193):
4 partially pandiagonal squares Frénicle N° 105, 439, 442 and 786, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
4 partially pandiagonal squares Frénicle N° 105, 439, 442 and 786, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.2.02 (index n° T4.212):
4 partially pandiagonal squares Frénicle N° 118, 271, 272 and 486, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
4 partially pandiagonal squares Frénicle N° 118, 271, 272 and 486, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.2.03 (index n° T4.214):
4 partially pandiagonal squares Frénicle N° 180, 347, 349 and 538, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.2.04 (index n° T4.188):
4 partially pandiagonal squares Frénicle N° 200, 737, 765 and 868, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.2.05 (index n° T4.189):
4 partially pandiagonal squares Frénicle N° 207, 736, 775 and 831, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.2.06 (index n° T4.195):
4 partially pandiagonal squares Frénicle N° 208, 525, 526 and 693, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
4 partially pandiagonal squares Frénicle N° 208, 525, 526 and 693, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.2.07 (index n° T4.060):
4 partially pandiagonal squares Frénicle N° 283, 472, 588 and 795, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
4 partially pandiagonal squares Frénicle N° 283, 472, 588 and 795, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.2.08 (index n° T4.141):
4 partially pandiagonal squares Frénicle N° 303, 509, 510 and 644, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
4 partially pandiagonal squares Frénicle N° 303, 509, 510 and 644, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.2.09 (index n° T4.234):
4 partially pandiagonal squares Frénicle N° 371, 551, 552 and 701, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
4 partially pandiagonal squares Frénicle N° 371, 551, 552 and 701, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.2.10 (index n° T4.123):
4 partially pandiagonal squares Frénicle N° 390, 571, 782 and 867, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
4 partially pandiagonal squares Frénicle N° 390, 571, 782 and 867, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.2.11 (index n° T4.221):
4 partially pandiagonal squares Frénicle N° 407, 531, 692 and 711, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
4 partially pandiagonal squares Frénicle N° 407, 531, 692 and 711, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.2.12 (index n° T4.161):
4 partially pandiagonal squares Frénicle N° 408, 555, 783 and 829, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
Total : 12 partially pandiagonal tori type 3.2 that display 48 partially pandiagonal squares, 144 semi-magic squares, and 96 sub-magic 2x2 squares.
Half of the displayed partially pandiagonal squares are Dudeney type VII and the other half are Dudeney type IX.
T4.03.3 Partially pandiagonal Tori Type 3.3
with 4 crossed magic diagonals producing 4 magic intersections and 4 non magic intersections.
Each torus type 3.3 is entirely covered by 8 sub-magic 2x2 squares.
All of the displayed partially pandiagonal squares are Dudeney type XI.
T4.03.3.1 (index n° T4.217):
4 partially pandiagonal squares Frénicle N° 181, 374, 484 and 643, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
4 partially pandiagonal squares Frénicle N° 181, 374, 484 and 643, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.03.3.2 (index n° T4.187):
4 partially pandiagonal squares Frénicle N° 202, 364, 689 and 724, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
4 partially pandiagonal squares Frénicle N° 202, 364, 689 and 724, and also 12 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
Total : 2 partially pandiagonal tori type 3.3 that display 8 partially pandiagonal squares, 24 semi-magic squares, and 16 sub-magic 2x2 squares.
All of the displayed partially pandiagonal squares are Dudeney type XI.
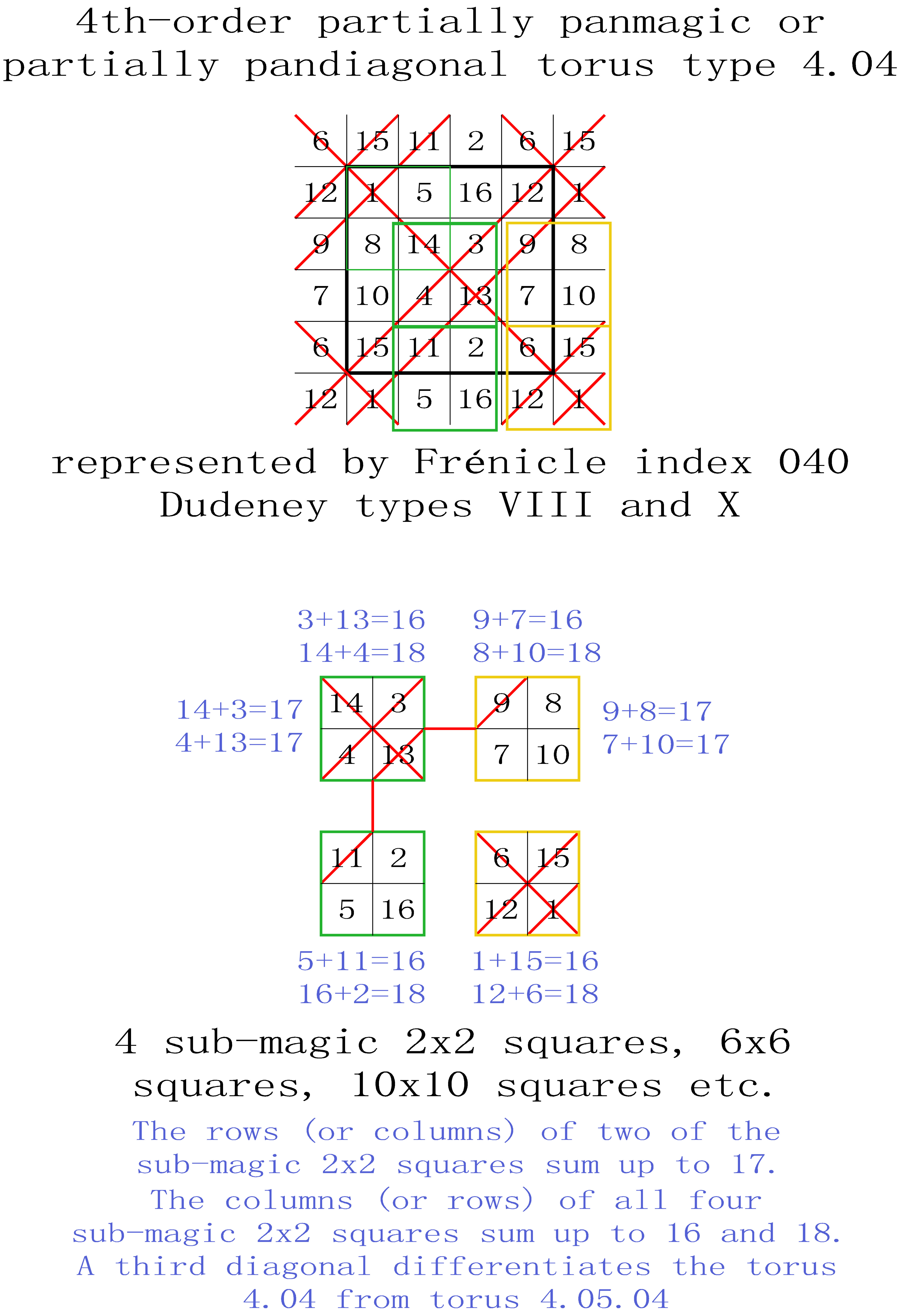
T4.04 Partially pandiagonal Tori Type 4
with 3 crossed magic diagonals producing 2 magic intersections and 2 non magic intersections
Each torus type 4 is entirely covered by 4 sub-magic 2x2 squares. Half of the displayed partially pandiagonal squares are Dudeney type VIII and the other half are Dudeney type X.
(tori identified thanks to Walter Trump's computing skills)
(tori identified thanks to Walter Trump's computing skills)
T4.04.1 (index n° T4.096):
2 partially pandiagonal squares Frénicle N° 40 and 522, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.04.2 (index n° T4.098):
2 partially pandiagonal squares Frénicle N° 275 and 519, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.04.3 (index n° T4.120):
2 partially pandiagonal squares Frénicle N° 542 and 866, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.04.4 (index n° T4.157):
2 partially pandiagonal squares Frénicle N° 727 and 865 and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
Total : 4 partially pandiagonal tori type 4 that display 8 partially pandiagonal squares, 56 semi-magic squares, and 16 sub-magic 2x2 squares
Half of the displayed partially pandiagonal squares are Dudeney type VIII and the other half are Dudeney type X.
Half of the displayed partially pandiagonal squares are Dudeney type VIII and the other half are Dudeney type X.
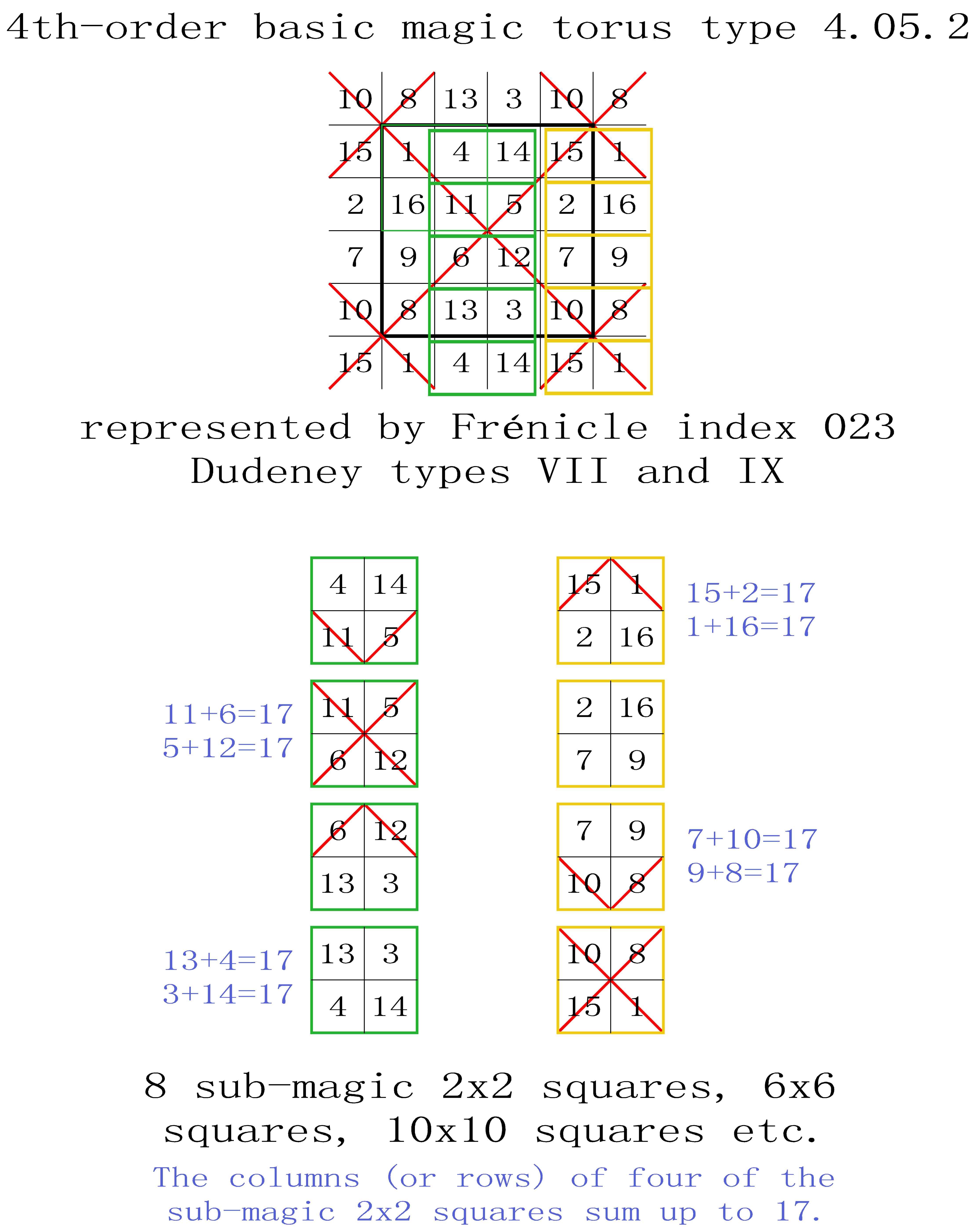
T4.05 Basic Magic Tori Type 5
with 2 crossed magic diagonals producing 2 magic intersections
Each torus type 5.1 and 5.2 is entirely covered by 8 sub-magic 2x2 squares.
Each torus type 5.3 and 5.4 is entirely covered by 4 sub-magic 2x2 squares.
T4.05.1 Basic Magic Tori Type 5.1
with 2 crossed magic diagonals producing 2 magic intersections.
Each torus type 5.1 is entirely covered by 8 sub-magic 2x2 squares.
All of the displayed magic squares are Dudeney type VI.
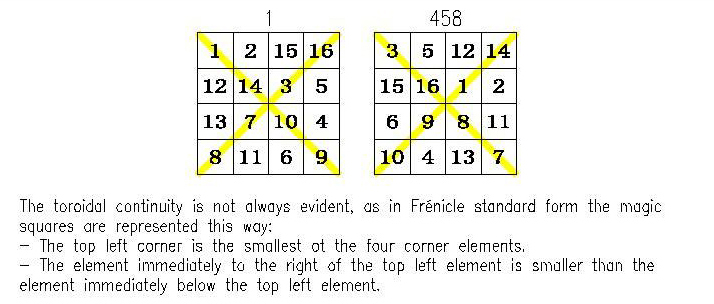
T4.05.1.01 (index n° T4.002):
2 magic squares Frénicle N° 1 and 458, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.02 (index n° T4.001):
2 magic squares Frénicle N° 2 and 448, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.03 (index n° T4.012):
2 magic squares Frénicle N° 4 and 672, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.04 (index n° T4.008):
2 magic squares Frénicle N° 5 and 625, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.05 (index n° T4.011):
2 magic squares Frénicle N° 6 and 611, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.06 (index n° T4.007):
2 magic squares Frénicle N° 7 and 612, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.07 (index n° T4.034):
2 magic squares Frénicle N° 12 and 520, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.08 (index n° T4.035):
2 magic squares Frénicle N° 13 and 339, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.09 (index n° T4.025):
2 magic squares Frénicle N° 14 and 457, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.10 (index n° T4.029):
2 magic squares Frénicle N° 15 and 258, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.11 (index n° T4.089):
2 magic squares Frénicle N° 36 and 742, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.12 (index n° T4.062):
2 magic squares Frénicle N° 37 and 832, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.13 (index n° T4.088):
2 magic squares Frénicle N° 38 and 706, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.14 (index n° T4.043):
2 magic squares Frénicle N° 39 and 826, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.15 (index n° T4.103):
2 magic squares Frénicle N° 44 and 352, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.16 (index n° T4.107):
2 magic squares Frénicle N° 45 and 557, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.17 (index n° T4.109):
2 magic squares Frénicle N° 47 and 556, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.18 (index n° T4.063):
2 magic squares Frénicle N° 51 and 772, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.19 (index n° T4.114):
2 magic squares Frénicle N° 52 and 222, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.20 (index n° T4.100):
2 magic squares Frénicle N° 53 and 223, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.21 (index n° T4.148):
2 magic squares Frénicle N° 70 and 391, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.22 (index n° T4.149):
2 magic squares Frénicle N° 71 and 359, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.23 (index n° T4.132):
2 magic squares Frénicle N° 72 and 745, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.24 (index n° T4.066):
2 magic squares Frénicle N° 75 and 857, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.25 (index n° T4.119):
2 magic squares Frénicle N° 78 and 725, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.26 (index n° T4.047):
2 magic squares Frénicle N° 79 and 856, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.27 (index n° T4.046):
2 magic squares Frénicle N° 80 and 760, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.28 (index n° T4.118):
2 magic squares Frénicle N° 81 and 430, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.29 (index n° T4.171):
2 magic squares Frénicle N° 86 and 363, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.30 (index n° T4.172):
2 magic squares Frénicle N° 87 and 318, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.31 (index n° T4.243):
2 magic squares Frénicle N° 127 and 220, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.32 (index n° T4.136):
2 magic squares Frénicle N° 130 and 561, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.33 (index n° T4.134):
2 magic squares Frénicle N° 131 and 624, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.34 (index n° T4.072):
2 magic squares Frénicle N° 133 and 807, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.35 (index n° T4.071):
2 magic squares Frénicle N° 134 and 830, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T 4.05.1.36 (index n° T4.244):
2 magic squares Frénicle N° 135 and 219, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.37 (index n° T4.052):
2 magic squares Frénicle N° 138 and 825, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.38 (index n° T4.124):
2 magic squares Frénicle N° 139 and 610, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.39 (index n° T4.227):
2 magic squares Frénicle N° 143 and 627, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.40 (index n° T4.232):
2 magic squares Frénicle N° 144 and 631, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.41 (index n° T4.253):
2 magic squares Frénicle N° 151 and 286, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.42 (index n° T4.211):
2 magic squares Frénicle N° 152 and 454, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.43 (index n° T4.202):
2 magic squares Frénicle N° 153 and 447, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.44 (index n° T4.252):
2 magic squares Frénicle N° 156 and 284, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.45 (index n° T4.057):
2 magic squares Frénicle N° 157 and 801, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.46 (index n° T4.248):
2 magic squares Frénicle N° 158 and 428, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.47 (index n° T4.076):
2 magic squares Frénicle N° 166 and 848, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.48 (index n° T4.058):
2 magic squares Frénicle N° 167 and 846, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.49 (index n° T4.192):
2 magic squares Frénicle N° 168 and 609, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.50 (index n° T4.140):
2 magic squares Frénicle N° 186 and 683, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.51 (index n° T4.254):
2 magic squares Frénicle N° 188 and 295, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.52 (index n° T4.128):
2 magic squares Frénicle N° 189 and 533, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.53 (index n° T4.250):
2 magic squares Frénicle N° 190 and 474, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.54 (index n° T4.207):
2 magic squares Frénicle N° 194 and 480, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.55 (index n° T4.129):
2 magic squares Frénicle N° 198 and 680, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.56 (index n° T4.196):
2 magic squares Frénicle N° 199 and 629, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.57 (index n° T4.004):
2 magic squares Frénicle N° 210 and 656, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.58 (index n° T4.003):
2 magic squares Frénicle N° 211 and 619, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.59 (index n° T4.225):
2 magic squares Frénicle N° 218 and 707, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.60 (index n° T4.131):
2 magic squares Frénicle N° 221 and 653, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.61 (index n° T4.229):
2 magic squares Frénicle N° 252 and 743, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.62 (index n° T4.247):
2 magic squares Frénicle N° 254 and 740, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.63 (index n° T4.065):
2 magic squares Frénicle N° 257 and 841, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.64 (index n° T4.045):
2 magic squares Frénicle N° 314 and 821, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.65 (index n° T4.024):
2 magic squares Frénicle N° 315 and 597, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.66 (index n° T4.139):
2 magic squares Frénicle N° 336 and 747, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.67 (index n° T4.074):
2 magic squares Frénicle N° 338 and 861, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.68 (index n° T4.150):
2 magic squares Frénicle N° 370 and 639, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.69 (index n° T4.147):
2 magic squares Frénicle N° 381 and 614, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.70 (index n° T4.054):
2 magic squares Frénicle N° 382 and 849, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.71 (index n° T4.037):
2 magic squares Frénicle N° 383 and 594, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.72 (index n° T4.126):
2 magic squares Frénicle N° 397 and 694, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.73 (index n° T4.112):
2 magic squares Frénicle N° 398 and 626, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.74 (index n° T4.215):
2 magic squares Frénicle N° 404 and 641, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.75 (index n° T4.218):
2 magic squares Frénicle N° 427 and 718, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.76 (index n° T4.102):
2 magic squares Frénicle N° 429 and 673, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.77 (index n° T4.223):
2 magic squares Frénicle N° 452 and 750, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.78 (index n° T4.028):
2 magic squares Frénicle N° 502 and 596, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.79 (index n° T4.176):
2 magic squares Frénicle N° 516 and 752, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.80 (index n° T4.039):
2 magic squares Frénicle N° 547 and 593, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.81 (index n° T4.166):
2 magic squares Frénicle N° 573 and 697, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.82 (index n° T4.152):
2 magic squares Frénicle N° 574 and 634, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.83 (index n° T4.041):
2 magic squares Frénicle N° 595 and 804, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.84 (index n° T4.042):
2 magic squares Frénicle N° 602 and 764, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.85 (index n° T4.185):
2 magic squares Frénicle N° 615 and 815, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.86 (index n° T4.163):
2 magic squares Frénicle N° 665 and 777, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.87 (index n° T4.162):
2 magic squares Frénicle N° 739 and 755, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.88 (index n° T4.167):
2 magic squares Frénicle N° 751 and 776, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.89 (index n° T4.200):
2 magic squares Frénicle N° 756 and 862, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.90 (index n° T4.203):
2 magic squares Frénicle N° 769 and 864, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.91 (index n° T4.113):
2 magic squares Frénicle N° 813 and 819, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.1.92 (index n° T4.153):
2 magic squares Frénicle N° 816 and 833, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
Total : 92 basic magic tori type 5.1 that display 184 basic magic squares, 1,288 semi-magic squares, and 736 sub-magic 2x2 squares
All of the displayed basic magic squares are Dudeney type VI.
All of the displayed basic magic squares are Dudeney type VI.
T4.05.2 Basic Magic Tori Type 5.2
with 2 crossed magic diagonals producing 2 magic intersections.
Each torus type 5.2 is entirely covered by 8 sub-magic 2x2 squares.
Half of the displayed magic squares are Dudeney type VII and the other half are Dudeney type IX.
T4.05.2.01 (index n° T4.049):
2 magic squares Frénicle N° 23 and 767, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.02 (index n° T4.068):
2 magic squares Frénicle N° 29 and 781, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.03 (index n° T4.026):
2 magic squares Frénicle N° 59 and 870, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.04 (index n° T4.249):
2 magic squares Frénicle N° 142 and 438, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.05 (index n° T4.228):
2 magic squares Frénicle N° 145 and 529, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.06 (index n° T4.219):
2 magic squares Frénicle N° 161 and 703, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.07 (index n° T4.040):
2 magic squares Frénicle N° 172 and 869, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.08 (index n° T4.255):
2 magic squares Frénicle N° 193 and 268, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.09 (index n° T4.206):
2 magic squares Frénicle N° 197 and 346, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.10 (index n° T4.197):
2 magic squares Frénicle N° 205 and 700, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.11 (index n° T4.122):
2 magic squares Frénicle N° 215 and 799, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.12 (index n° T4.251):
2 magic squares Frénicle N° 235 and 845, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.13 (index n° T4.032):
2 magic squares Frénicle N° 249 and 878, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.14 (index n° T4.142):
2 magic squares Frénicle N° 300 and 559, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.15 (index n° T4.061):
2 magic squares Frénicle N° 335 and 470, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.16 (index n° T4.199):
2 magic squares Frénicle N° 348 and 714, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.17 (index n° T4.033):
2 magic squares Frénicle N° 358 and 875, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.18 (index n° T4.233):
2 magic squares Frénicle N° 369 and 563, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.19 (index n° T4.209):
2 magic squares Frénicle N° 373 and 717, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.20 (index n° T4.210):
2 magic squares Frénicle N° 403 and 738, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.21 (index n° T4.205):
2 magic squares Frénicle N° 405 and 517, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.22 (index n° T4.156):
2 magic squares Frénicle N° 406 and 453, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.23 (index n° T4.160):
2 magic squares Frénicle N° 418 and 805, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.24 (index n° T4.245):
2 magic squares Frénicle N° 441 and 873, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.25 (index n° T4.154):
2 magic squares Frénicle N° 455 and 729, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.26 (index n° T4.191):
2 magic squares Frénicle N° 518 and 728, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.27 (index n° T4.222):
2 magic squares Frénicle N° 564 and 732, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.28 (index n° T4.230):
2 magic squares Frénicle N° 567 and 749, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.29 (index n° T4.110):
2 magic squares Frénicle N° 568 and 757, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.30 (index n° T4.075):
2 magic squares Frénicle N° 580 and 858, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.31 (index n° T4.055):
2 magic squares Frénicle N° 587 and 879, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
T4.05.2.32 (index n° T4.116):
2 magic squares Frénicle N° 733 and 758, and also 14 semi-magic squares. The torus is entirely covered by 8 sub-magic 2x2 squares.
Total : 32 basic magic tori type 5.2 that display 64 basic magic squares, 448 semi-magic squares, and 256 sub-magic 2x2 squares
Half of the displayed basic magic squares are Dudeney type VII and the other half are Dudeney type IX.
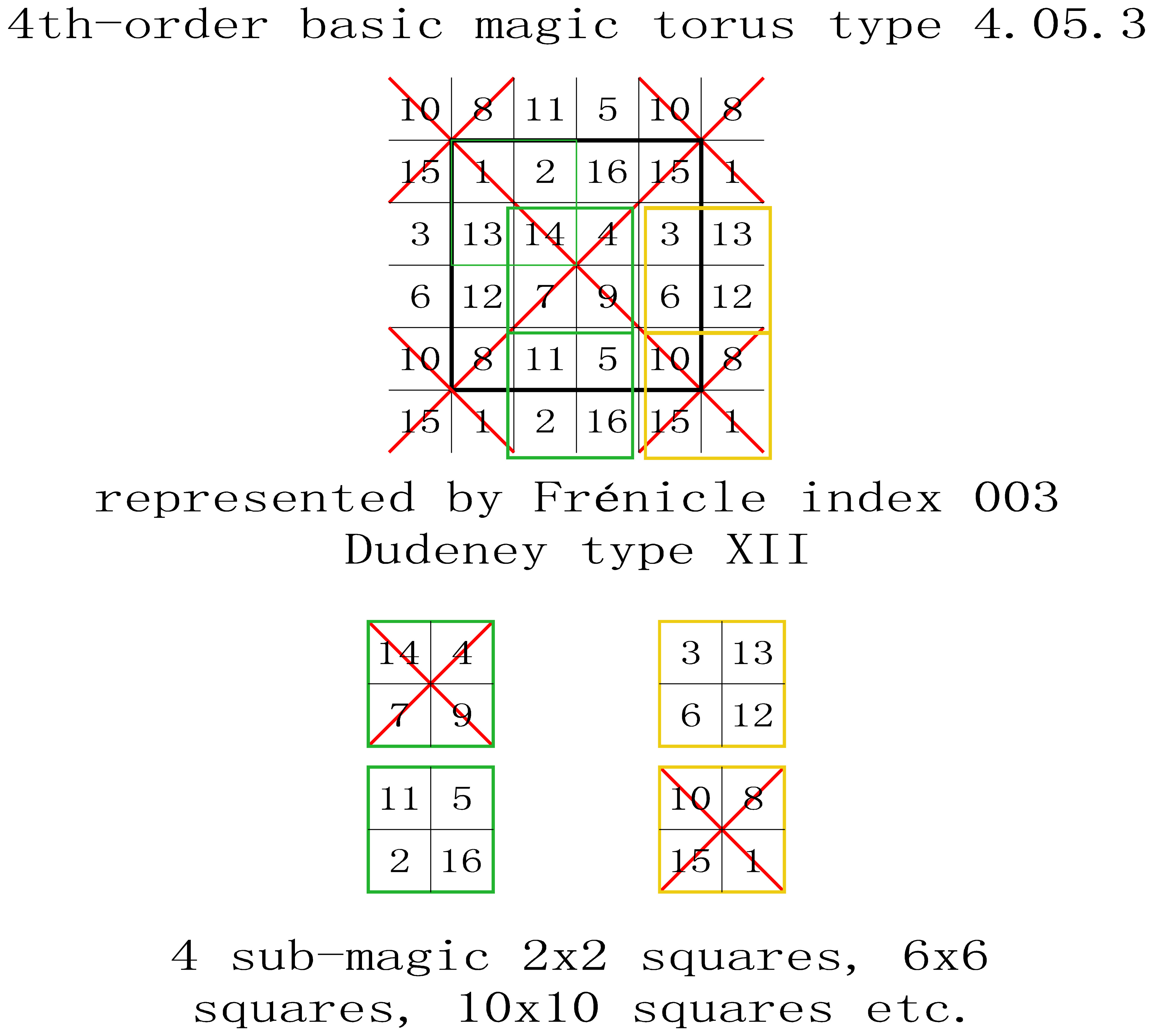
T4.05.3 Basic Magic Tori Type 5.3
with 2 crossed magic diagonals producing 2 magic intersections.
Each torus type 5.3 is entirely covered by 4 sub-magic 2x2 squares.
All of the displayed magic squares are Dudeney type XII.
T4.05.3.1 (index n° T4.005):
2 magic squares Frénicle N° 3 and 613, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.3.2 (index n° T4.170):
2 magic squares Frénicle N° 88 and 650, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.3.3 (index n° T4.006):
2 magic squares Frénicle N° 209 and 449, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.3.4 (index n° T4.159):
2 magic squares Frénicle N° 319 and 666, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
Total : 4 basic magic tori type 5.3 that display 8 basic magic squares, 56 semi-magic squares, and 16 sub-magic 2x2 squares
All of the displayed basic magic squares are Dudeney type XII
T4.05.4 Basic Magic Tori Type 5.4
with 2 crossed magic diagonals producing 2 magic intersections.
Each torus type 5.4 is entirely covered by 4 sub-magic 2x2 squares.
Half of the displayed magic squares are Dudeney type VIII and the other half are Dudeney type X.
T4.05.4.01 (index n° T4.019):
2 magic squares Frénicle N° 8 and 343, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.02 (index n° T4.018):
2 magic squares Frénicle N° 9 and 263, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.03 (index n° T4.022):
2 magic squares Frénicle N° 10 and 240, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.04 (index n° T4.017):
2 magic squares Frénicle N° 11 and 241, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.05 (index n° T4.050):
2 magic squares Frénicle N° 20 and 811, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.06 (index n° T4.069):
2 magic squares Frénicle N° 26 and 812, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.07 (index n° T4.097):
2 magic squares Frénicle N° 41 and 493, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.08 (index n° T4.095):
2 magic squares Frénicle N° 42 and 494, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.09 (index n° T4.092):
2 magic squares Frénicle N° 43 and 434, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.10 (index n° T4.078):
2 magic squares Frénicle N° 58 and 877, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.11 (index n° T4.182):
2 magic squares Frénicle N° 94 and 655, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.12 (index n° T4.177):
2 magic squares Frénicle N° 99 and 618, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.13 (index n° T4.239):
2 magic squares Frénicle N° 128 and 773, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.14 (index n° T4.240):
2 magic squares Frénicle N° 129 and 762, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.15 (index n° T4.083):
2 magic squares Frénicle N° 170 and 874, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.16 (index n° T4.237):
2 magic squares Frénicle N° 212 and 794, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.17 (index n° T4.242):
2 magic squares Frénicle N° 232 and 863, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.18 (index n° T4.020):
2 magic squares Frénicle N° 238 and 411, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.19 (index n° T4.015):
2 magic squares Frénicle N° 239 and 412, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.20 (index n° T4.208):
2 magic squares Frénicle N° 242 and 546, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.21 (index n° T4.105):
2 magic squares Frénicle N° 243 and 501, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.22 (index n° T4.014):
2 magic squares Frénicle N° 244 and 415, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.23 (index n° T4.010):
2 magic squares Frénicle N° 245 and 416, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.24 (index n° T4.082):
2 magic squares Frénicle N° 248 and 872, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.25 (index n° T4.016):
2 magic squares Frénicle N° 260 and 410, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.26 (index n° T4.099):
2 magic squares Frénicle N° 276 and 491, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.27 (index n° T4.086):
2 magic squares Frénicle N° 277 and 685, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.28 (index n° T4.031):
2 magic squares Frénicle N° 278 and 601, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.29 (index n° T4.179):
2 magic squares Frénicle N° 327 and 616, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.30 (index n° T4.180):
2 magic squares Frénicle N° 332 and 652, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.31 (index n° T4.021):
2 magic squares Frénicle N° 340 and 409, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.32 (index n° T4.236):
2 magic squares Frénicle N° 353 and 770, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.33 (index n° T4.104):
2 magic squares Frénicle N° 354 and 823, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.34 (index n° T4.081):
2 magic squares Frénicle N° 357 and 871, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.35 (index n° T4.013):
2 magic squares Frénicle N° 413 and 607, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.36 (index n° T4.009):
2 magic squares Frénicle N° 414 and 608, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.37 (index n° T4.238):
2 magic squares Frénicle N° 417 and 796, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.38 (index n° T4.093):
2 magic squares Frénicle N° 431 and 686, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.39 (index n° T4.190):
2 magic squares Frénicle N° 437 and 814, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.40 (index n° T4.241):
2 magic squares Frénicle N° 440 and 880, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.41 (index n° T4.094):
2 magic squares Frénicle N° 492 and 688, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.42 (index n° T4.030):
2 magic squares Frénicle N° 495 and 598, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.43 (index n° T4.090):
2 magic squares Frénicle N° 496 and 754, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.44 (index n° T4.087):
2 magic squares Frénicle N° 497 and 684, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.45 (index n° T4.106):
2 magic squares Frénicle N° 500 and 606, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.46 (index n° T4.235):
2 magic squares Frénicle N° 541 and 759, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.47 (index n° T4.135):
2 magic squares Frénicle N° 544 and 605, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.48 (index n° T4.070):
2 magic squares Frénicle N° 579 and 847, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.49 (index n° T4.056):
2 magic squares Frénicle N° 585 and 800, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.50 (index n° T4.051):
2 magic squares Frénicle N° 586 and 876, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.51 (index n° T4.091):
2 magic squares Frénicle N° 687 and 753, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
T4.05.4.52 (index n° T4.117):
2 magic squares Frénicle N° 726 and 820, and also 14 semi-magic squares. The torus is entirely covered by 4 sub-magic 2x2 squares.
Total : 52 basic magic tori type 5.4 that display 104 basic magic squares, 728 semi-magic squares, and 208 sub-magic 2x2 squares.
Half of the displayed basic magic squares are Dudeney type VIII and the other half are Dudeney type X.
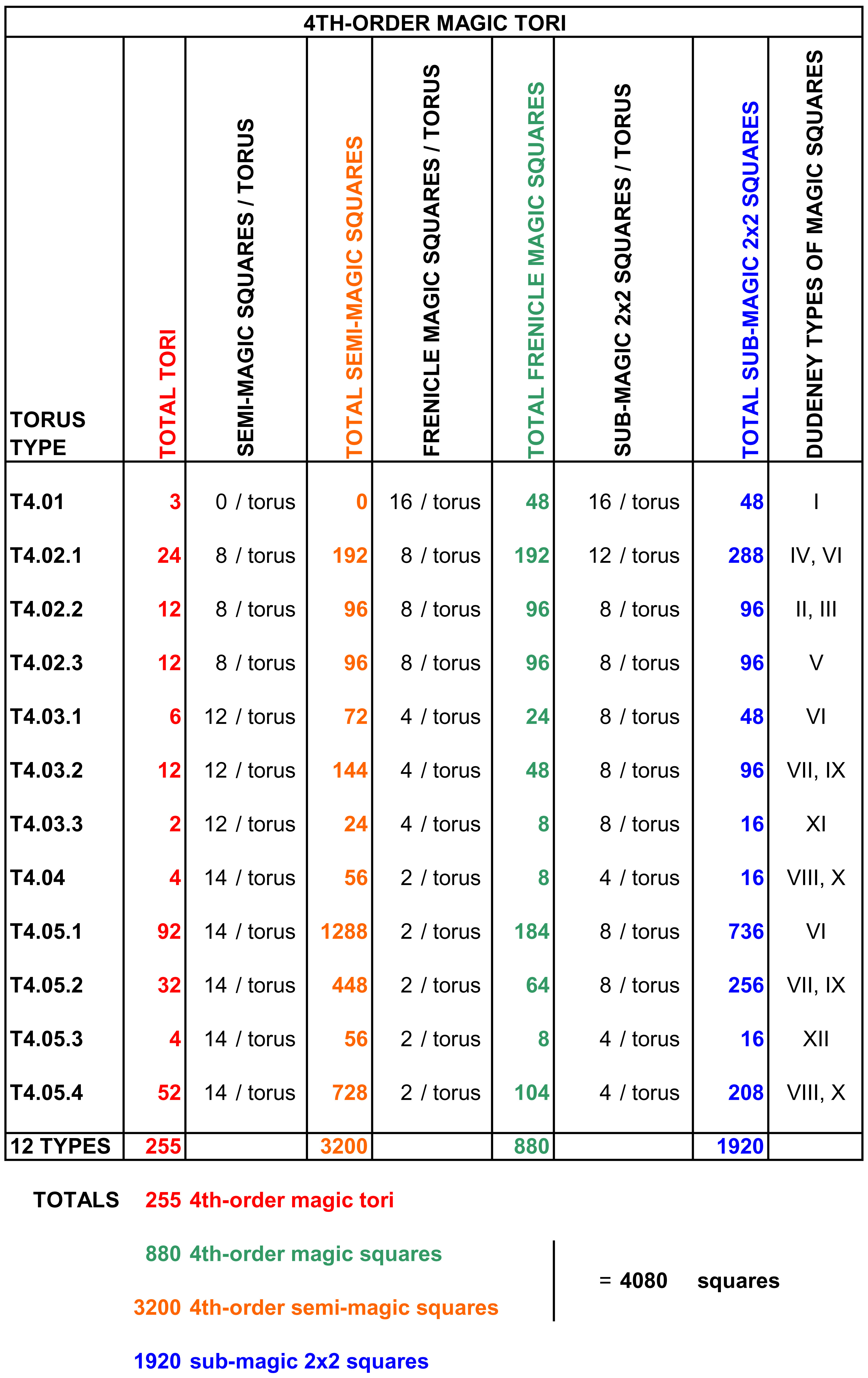
Grand Totals of the 4th-Order Magic Tori :
255 FOURTH-ORDER MAGIC TORI THAT DISPLAY 880 MAGIC SQUARES,
3 200 SEMI-MAGIC SQUARES, AND 1 920 SUB-MAGIC 2x2 SQUARES
Fourth-order Semi-Magic Tori
A semi-magic square is a square that contains arithmetical magic in all of its rows and columns, but not in both of its main diagonals.
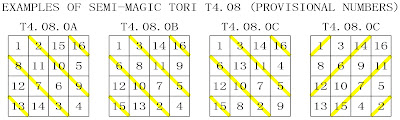
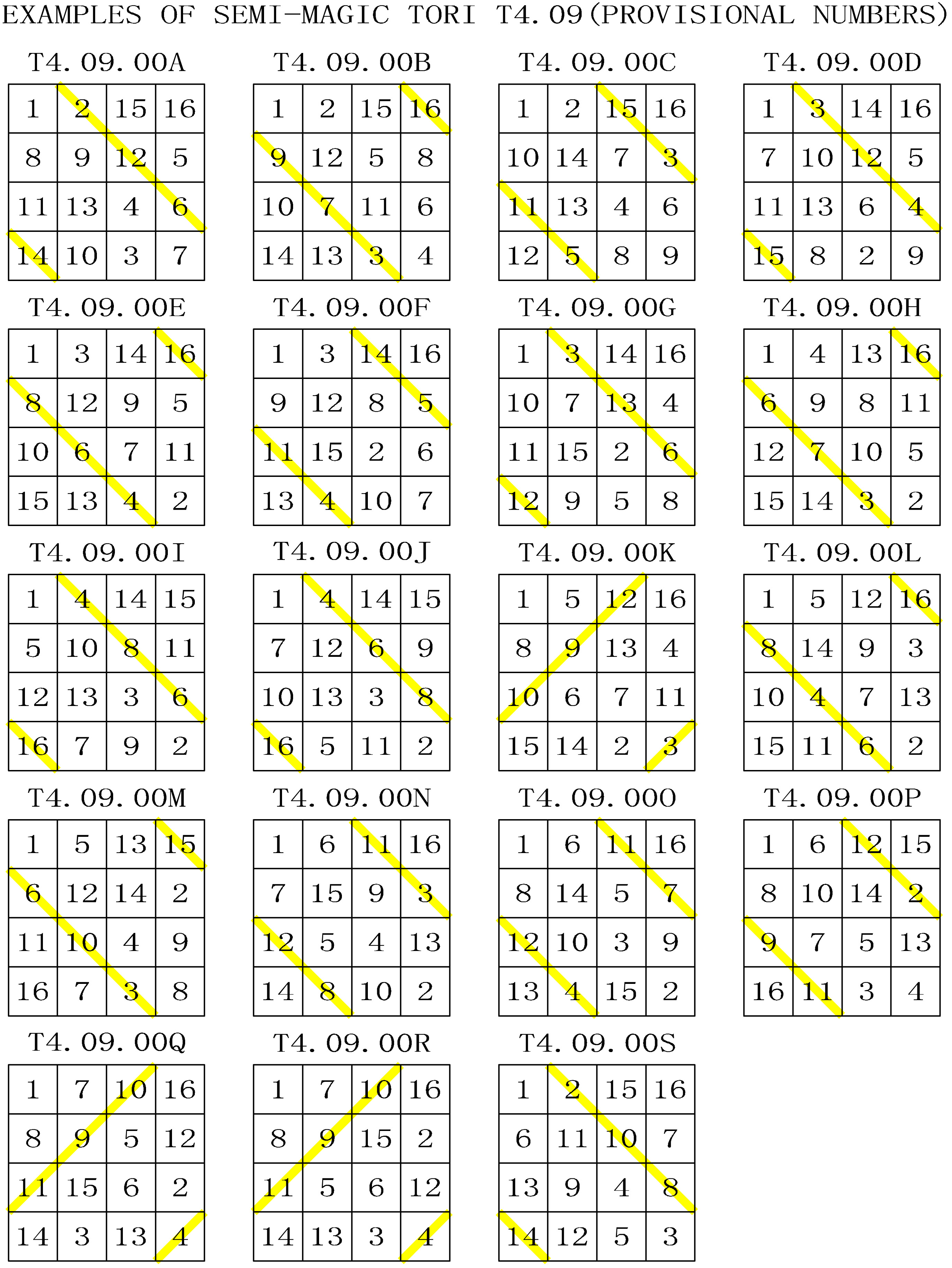
According to Walter Trump's first computer calculations the number of semi-magic and magic squares is 68,688. 68,688 - 880 magic squares = 67,808 semi-magic squares. 3,200 semi-magic squares are already displayed on the 255 magic tori. We can deduce that there are also 67,808 – 3,200 = 64,608 4th-order semi-magic squares displayed on another 4,038 semi-magic tori (64,608 / 16). The semi-magic tori could have crossed magic diagonals that do not produce magic intersections, parallel magic diagonals (without magic intersections), or no magic diagonals at all. Walter Trump's latest computer programme confirms that the fourth-order semi-magic tori either have parallel magic diagonals that produce no magic intersections, or no magic diagonals at all. Some examples of the different types (provisionally represented here by a single square for each torus) are shown below:
According to Walter Trump's first computer calculations the number of semi-magic and magic squares is 68,688. 68,688 - 880 magic squares = 67,808 semi-magic squares. 3,200 semi-magic squares are already displayed on the 255 magic tori. We can deduce that there are also 67,808 – 3,200 = 64,608 4th-order semi-magic squares displayed on another 4,038 semi-magic tori (64,608 / 16). The semi-magic tori could have crossed magic diagonals that do not produce magic intersections, parallel magic diagonals (without magic intersections), or no magic diagonals at all. Walter Trump's latest computer programme confirms that the fourth-order semi-magic tori either have parallel magic diagonals that produce no magic intersections, or no magic diagonals at all. Some examples of the different types (provisionally represented here by a single square for each torus) are shown below:
T4.06 Semi-Magic Tori Type 6
with 4 parallel magic diagonals producing no magic intersections
Total : 12 semi-magic tori type 6 that display 192 semi-magic squares
(semi-magic tori counted by Walter Trump's computer calculations)
T4.07 Semi-Magic Tori Type 7
with 2 unequally spaced parallel magic diagonals producing no magic intersections
Total : 12 semi-magic tori type 7 that display 192 semi-magic squares
(semi-magic tori counted by Walter Trump's computer calculations)
T4.08 Semi-Magic Tori Type 8
with 2 equally spaced parallel magic diagonals producing no magic intersections
Total : 88 semi-magic tori type 8 that display 1,408 semi-magic squares
(semi-magic tori counted by Walter Trump's computer calculations)
T4.09 Semi-Magic Tori Type 9
with a single magic diagonal producing no magic intersection
Total : 200 semi-magic tori type 9 that display 3,200 semi-magic squares
(semi-magic tori counted by Walter Trump's computer calculations)
T4.10 Semi-Magic Tori Type 10
with no magic diagonals
Total : 3,726 semi-magic tori type 10 that display 59,616 semi-magic squares
(semi-magic tori counted by Walter Trump's computer calculations)
The study remains to be completed by listing all the semi-magic tori in numerical order (using Frénicle standard form for example).
Grand Totals of the 4th-Order Semi-Magic Tori :
4,038 FOURTH-ORDER SEMI-MAGIC TORI THAT DISPLAY 64,608 SEMI-MAGIC SQUARES
Magic and Semi-Magic 4th-Order Tori : Conclusions
The study of the table of 880 4th-order magic squares reveals the existence of 255 magic tori, that not only display 880 magic squares, but also 3,200 semi-magic squares. All of the 255 magic tori are entirely covered by 2x2 sub-magic squares. There is a total of 1,920 sub-magic 2x2 squares on the 255 magic tori.
The number of N-order squares (magic and semi-magic squares) that are displayed on each N-order magic torus = N².
4,038 semi-magic 4th-order tori have also been found, and these display a further 64,608 semi-magic squares. The sub-magic 2x2 squares of the 4th-order semi-magic tori have yet to be enumerated.
255 is now the fourth number of the sequence A270876 "Number of magic tori of order n composed of the numbers from 1 to n^2," published by the On-Line Encyclopedia of Integer Sequences (OEIS).
4,293 (255 + 4,038) is now the fourth number of the sequence A271104 "Number of magic and semi-magic tori of order n composed of the numbers from 1 to n^2," published by the On-Line Encyclopedia of Integer Sequences (OEIS).
T3 Third-Order Magic Torus
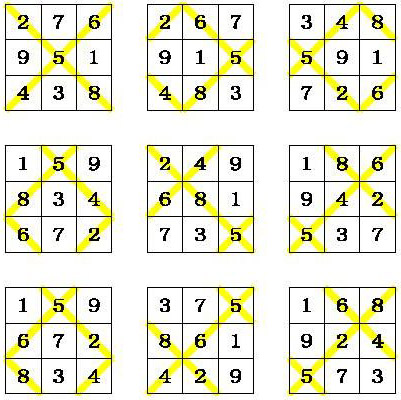
The study would not be complete without examining the unique 3rd-order magic torus. Beginning with the 3x3 magic square in Frénicle standard form (at the top left of the following illustration), and taking into account the scrolling effect on the 3rd order magic torus we obtain another eight 3rd-order semi-magic squares:
After transformation of these semi-magic squares into Frénicle standard form we obtain:
The 3rd-order magic torus displays just one magic square. Although there are two crossed magic diagonals on the torus, they only produce a single magic intersection over the number 5, whilst the second intersection occurs in the interval between the numbers 6, 4, 8 and 2. It is interesting to note that the mean number of 6+4+8+2 is 5, and that the mean numbers of the couples 6+4 and 8+2 are also 5.
We can deduce that basic (not pandiagonal, semi-pandiagonal or partially pandiagonal) odd number N-order tori display not only 1 basic N-order magic square, but also N²-1 semi-magic N-order squares. For example, the smallest 1st-order magic torus displays 1 basic 1st-order magic square and 1²-1=0 semi-magic 1st-order squares. It is interesting to note that the first-order magic torus can be visualised either as a basic magic torus, or even as a pandiagonal torus!
1, (the number of third-order magic tori), is now the third number of the sequences A270876 "Number of magic tori of order n composed of the numbers from 1 to n^2" and A271104 "Number of magic and semi-magic tori of order n composed of the numbers from 1 to n^2," published by the On-Line Encyclopedia of Integer Sequences (OEIS).
Posted on the 21st January 2018, an article entitled "Multiplicative Magic Tori" shows that the 255 magic tori of order-4 are different multiplied states of 82 Multiplicative Magic Tori (MMT) of order-4!
I wish to express my gratitude to Walter Trump, not only for his valuable advice concerning the choice of terminology, but also for his computing skills that identified the magic torus type 4.04, and enabled a precise count.
New development!
Posted on the 21st January 2018, an article entitled "Multiplicative Magic Tori" shows that the 255 magic tori of order-4 are different multiplied states of 82 Multiplicative Magic Tori (MMT) of order-4!
Acknowledgements
I wish to express my gratitude to Walter Trump, not only for his valuable advice concerning the choice of terminology, but also for his computing skills that identified the magic torus type 4.04, and enabled a precise count.
I wish to thank Miguel Angel Amela who very kindly programmed a count of 4x4 broken diagonal solutions of the fourth-order magic squares, the results of which confirm the findings of the above study.
Since publishing this study I have become aware of Aale de Winkel's "Magic Encyclopedia" database Order 04 square group theory. I wish to belatedly acknowledge Aale de Winkel's work, which, although quite different to mine, (we neither use the same reasoning nor come to the same conclusion), is complementary. Please note that in his study Aale de Winkel uses analytic numbers ranging from 0 to 15 instead of the regular numbers 1 to 16. This does not change the magical properties of the squares but you need to add 1 to each number to see the traditional Frénicle versions.
I wish to thank Kanji Setsuda for pointing out the importance of associated or self-complementary magic squares. This has lead me to create a specific subdivision of the semi-pandiagonal tori.
My thanks also go to Dwane Campbell, who has published a very interesting comparative study of the Dudeney and Walkington Order-4 magic square classifications in the three pages that follow:
"Analysis of Order-4 Magic Squares,"
"Order-4 Magic Squares Grouped by Base Square Quartets,"
"Features in Order-4 Magic Squares."
My thanks also go to Dwane Campbell, who has published a very interesting comparative study of the Dudeney and Walkington Order-4 magic square classifications in the three pages that follow:
"Analysis of Order-4 Magic Squares,"
"Order-4 Magic Squares Grouped by Base Square Quartets,"
"Features in Order-4 Magic Squares."