List of the 880 Frénicle Magic Squares of Order-4

Bernard Frénicle de Bessy was the first to determine that there were 880 essentially different magic squares of order-4, and his findings were published posthumously in the "Table Générale des Quarrez Magiques de Quatre," in 1693.

Title of Frénicle's study of magic squares published in 1693

The "Table Générale des Quarrez Magiques de Quatre" published in 1693

It was more than 300 years later, that it was discovered that these 880 magic squares of order-4 were displayed on 255 magic tori of order-4. At first listed by type in 2011, the 255 magic tori of order-4 were later given additional index numbers in a "Table of Fourth-Order Magic Tori" in 2012. In 2019 some of the magic tori of order-4 were found to be extra-magic, with nodal intersections of 4 or more magic lines and / or knight move magic diagonals. Other studies of the magic tori of order-4 have included sub-magic 2 x 2 squares (in 2013), magic torus complementary number patterns (in 2017), and even and odd number patterns (in 2019). Then after a gap of 5 years, the magic tori have been found to belong to 137 plus or minus groups (in 2024).

It has become increasingly important to provide an easily accessible document that recapitulates these different findings. I have therefore compiled the following "List of the 880 Frénicle Indexed Magic Squares of Order-4," with their corresponding Dudeney types and also full details of the magic tori:

Read more ...

Paired and Self-Complementary Magic Tori of Order-4

In his paper "Self-complementary magic squares of 4x4," Mutsumi Suzuki has shown that there are 352 self-complementary magic squares of order-4. Although Suzuki does not use Frénicle standard form, his examples are essentially different, and the total of these 352 self-complementary squares can therefore be compared with the grand total of the 880 essentially different magic squares of order-4 previously identified by Bernard Frénicle de Bessy.

On his page "Self-Similar Magic Squares," Harvey Heinz has studied Mutsumi Suzuki’s work, and points out that the 352 self-complementary magic squares include 48 Dudeney Type III associated semi-pandiagonal, 96 Dudeney Type VI semi-pandiagonal, and 208 Dudeney Type VI “simple” magic squares. The Dudeney Types referred to by Harvey Heinz come from Henry Dudeney’s classification of the 880 Frénicle magic squares into 12 types, each of which corresponds to a different complementary number pattern.

Today we know that the 880 Frénicle indexed magic squares are partial viewpoints of 255 essentially different magic tori of Order-4 (OEIS sequence A270876). A previous post "Complementary Number Patterns on Fourth-Order Magic Tori" has shown that some of the 12 Dudeney complementary number patterns become redundant on fourth-order magic tori, and this has resulted in the creation of a new reduced set of complementary number pattern types which are better adapted:

Therefore, with less complementary number patterns, what are the implications for the totals of self-complementary and paired complementary magic tori of order-4? In the study that follows, all of the 255 magic tori of order-4 are listed, and the details of their complements are given. In the final observations, the different cases of self-complementarity or paired complementarity are analysed, together with the respective complementary number patterns.

Please note that if you click on the button that appears at the top right hand side of the pdf viewer below, a new window will open and full size pages of the paper "Self-Complementary and Paired Complementary Magic Tori of Order-4" will then be displayed, with options for zooming.

Read more ...

Pandiagonality of the Squared Matrices of Associative and Related Magic Squares

The present study is inspired by Miguel Angel Amela's paper dated September 2016, entitled "Powers of Associative Magic Squares," and by Francis Gaspalou's paper dated 7th October 2016, entitled "Note on the features of the associative magic squares which give magic solutions when raised at an even power."

Both of these studies refer to an earlier paper by Charles K. Cook, Michael R. Bacon, and Rebecca A. Hillman; “The Magicness of Powers of Some Magic Squares,” published in The Fibonacci Quarterly, Volume 48, Number 4; 2010.

Pandiagonality of the Squared Matrices of Associative and Related Magic Squares

In the present study, which approaches the subject from a magic torus viewpoint, the use of formulae for generation enables an analysis of comparable magic tori throughout the different doubly-even and odd-orders. Please note that there are no associative magic squares of singly-even-orders, as demonstrated by C. Planck  in his "Pandiagonal magics of orders 6 and 10 with minimal numbers," published in "The Monist," Volume 29, N° 2 (April 1919), pages 307-316.

The pages that follow show that both associative and non-associative matrices can yield magic solutions when squared. Although the study was initially intended for associative magic squares only, other types of magic squares, displayed on related magic tori, are now also included for the sake of comparison.

The research also reveals that recurring pandiagonal patterns appear on the squared matrices, throughout the higher-orders of magic tori generated by a same formula.

1/4 pandiagonal squared matrix of an associative magic square viewpoint of an order-12 semi-pandiagonal magic torus

To view the paper "Pandiagonality of the Squared Matrices of Associative and Related Magic Squares," please note that if you click on the button that appears at the top right hand side of the pdf viewer below, a new window will open and full size pages will then be displayed, with options for zooming.

Read more ...

Magic Torus Coordinate and Vector Symmetries

Magic squares have fascinated mathematicians for centuries and they continue to do so today. However, many questions remain unanswered, and this study proposes a different perspective in order to shed new light on what magic squares are and how they work. Considering magic squares to be flattened partial viewpoints of convex or concave magic tori, the implied Gaussian surfaces require a modular arithmetic approach that is tested and analysed here.

Until today, most magic square construction methods use base squares, whilst "Magic Torus Coordinate and Vector Symmetries" proposes modular coordinate equations that not only define specific magic tori, but also generate their magic torus descendants.

The construction of Agrippa's traditional magic squares is analysed in detail for each of the seven planetary magic tori, and modular coordinate equations are defined that generate descendant tori throughout the respective higher-orders, whether they be odd, doubly-even, or singly-even.

The unique third-order magic torus and also a fifth-order pandiagonal torus of Latin construction are examined in detail. The modular coordinate equations that are defined generate an interesting variety of higher-odd-order descendant tori.

The study also explores the construction of the 12 different types of fourth-order magic tori, as well as the generation of their doubly-even magic torus descendants. In addition, a fourth-order Candy-style perfect square pandiagonal torus, and a fourth-order unidirectionally pandiagonal semi-magic torus, are each analysed in detail, and their torus descendants generated, throughout their respective higher-orders.

At the end of the study observations are made, and some conclusions are drawn as to the signification of the findings, and the potential for future research.

Some sample illustrations of a fourth-order partially pandiagonal torus and its partially pandiagonal torus descendants are shown below:

T4.195 4th-order partially pandiagonal torus

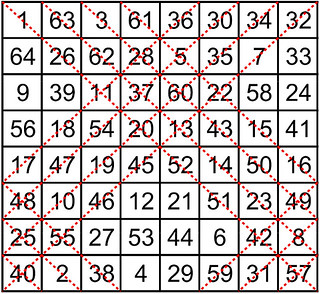8th-order partially pandiagonal torus, direct descendant of T4.195

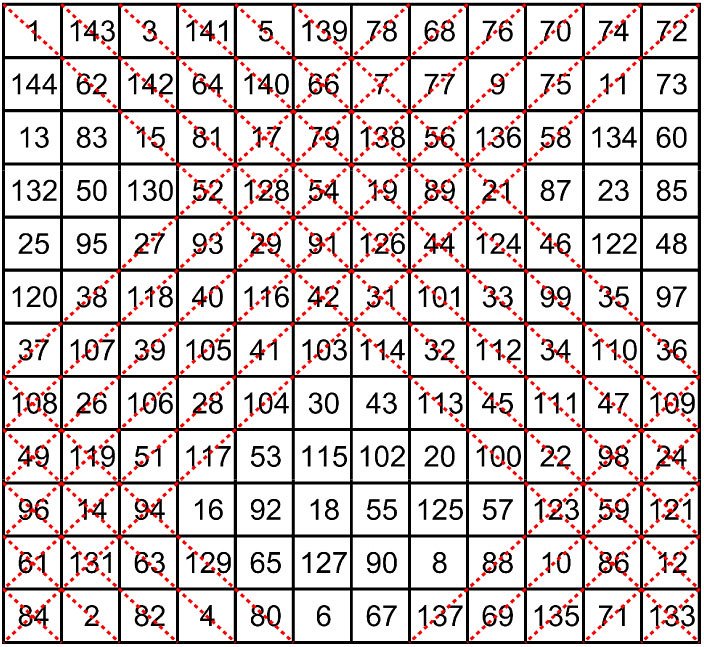12th-order partially pandiagonal torus, direct descendant of T4.195

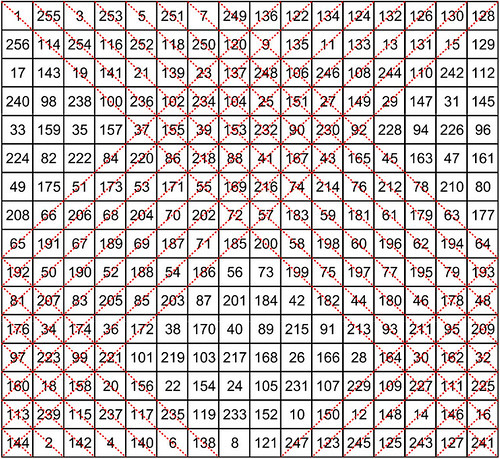16th-order partially pandiagonal torus, direct descendant of T4.195

To download "Magic Torus Coordinate and Vector Symmetries" from Google Drive, please use the following link: MTCVS 161019. The 134 Mo pdf file exceeds the maximum size (25 Mo) that Google Drive can scan, but as the file is virus free you can download it safely. Depending on the speed of your computer, the download can take up to two or three minutes to complete.

Read more ...

Complementary Number Patterns on Fourth-Order Magic Tori

The 880 fourth-order magic squares were first identified and listed by Bernard Frénicle de Bessy in his « Table générale des quarrez magiques de quatre, » which was published posthumously in 1693, in his book « Des quarrez magiques. » The census of these 880 4x4 squares is given in the appendix to the book « New Recreations With Magic Squares » by William H. Benson and Oswald Jacoby (Edition 1976), and also on the website of the late Harvey D. Heinz:  Frénicle n° 1 à 200, Frénicle n° 201 à 400, Frénicle n° 401 à 600, Frénicle n° 601 à 880.

Further to Bernard Frénicle de Bessy's initial findings, Henry Ernest Dudeney then classified the 880 fourth-order magic squares under 12 pattern types, in "The Queen" in 1910, (later republished in his book  "Amusements in Mathematics" in 1917). These patterns were determined through the observation of the relative positions of complementary pairs of numbers (which add up to N²+1 when N is the order of the square).

Although the different Dudeney pattern types can indeed be observed on fourth-order magic squares, they cannot be used for the classification of the fourth-order magic tori that display these squares. A Dudeney pattern type can be misleading because it depends on a bordered magic square viewpoint, whilst the magic torus that displays the magic square has a limitless surface...

In the study that follows the complementary number patterns are therefore tested, by comparing a developed torus surface and two traditional Frénicle magic square viewpoints for each of the 12 different types of fourth-order magic tori.

Complementary number patterns of each fourth-order magic torus type

General information on the magic torus index and type numbers

In addition to the Frénicle index numbers and the Dudeney types that have already been mentioned above, the present study also uses the index and type numbers of the fourth-order magic tori. For readers who may not be acquainted with the subject, essential information can be found in the following pages:

In a previous article "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus," the fourth-order magic tori have been classed in 12 types, and each magic torus has received a specific type number.

In a previous article "Table of Fourth-Order Magic Tori," so as to facilitate the identification of a magic torus beginning with any magic square, a standard torus form has also been defined, and each of the 255 fourth-order magic tori has received a specific index number.

Complementary number patterns of the pandiagonal tori type T4.01

The 3 pandiagonal tori type T4.01 are here represented by the pandiagonal torus with index n° T4.01.1 (torus type n° T4.01.1). This pandiagonal torus displays 16 pandiagonal squares with Frénicle index n°s 102, 104, 174, 201, 279, 281, 365, 393, 473, 530, 565, 623, 690, 748, 785 and 828. All of these squares, (including the Frénicle index n°s 102 and 174 illustrated here), show complementary number patterns that are Dudeney type I.

Complementary number patterns of the semi-pandiagonal tori type T4.02.1

The 24 semi-pandiagonal tori type T4.02.1 are here represented by the semi-pandiagonal torus with index n° T4.115 (torus type n° T4.02.1.09). This semi-pandiagonal torus displays 8 semi-pandiagonal squares with Frénicle index n°s 48, 192, 255, 400, 570, 734, 763 and 824. Half of these squares, (including the Frénicle index n° 192 illustrated here), show complementary number patterns that are Dudeney type IV. The other half, (including the Frénicle index n° 48 illustrated here), show complementary number patterns that are Dudeney type VI.

Complementary number patterns of the semi-pandiagonal tori type T4.02.2

The 12 semi-pandiagonal tori type T4.02.2 are here represented by the semi-pandiagonal torus with index n° T4.059 (torus type n° T4.02.2.01). This semi-pandiagonal torus displays 8 semi-pandiagonal squares with Frénicle index n°s 21, 176, 213, 361, 445, 591, 808 and 860. Half of these squares, (including the Frénicle index n° 21 illustrated here), show complementary number patterns that are Dudeney type II. The other half, (including the Frénicle index n° 176 illustrated here), show complementary number patterns that are Dudeney type III.

Complementary number patterns of the semi-pandiagonal tori type T4.02.3

The 12 semi-pandiagonal tori type T4.02.3 are here represented by the semi-pandiagonal torus with index n° T4.085 (torus type n° T4.02.3.01). This semi-pandiagonal torus displays 8 semi-pandiagonal squares with Frénicle index n°s 32, 173, 228, 362, 425, 577, 798 and 853. All of these squares, (including the Frénicle index n°s 173 and 228 illustrated here), show complementary number patterns that are Dudeney type V.

Complementary number patterns of the partially pandiagonal tori type T4.03.1

The 6 partially pandiagonal tori type T4.03.1 are here represented by the partially pandiagonal torus with index n° T4.108 (torus type n° T4.03.1.1). This partially pandiagonal torus displays 4 partially pandiagonal squares with Frénicle index n°s 46, 50, 337 and 545. All of these squares, (including the Frénicle index n°s 46 and 545 illustrated here), show complementary number patterns that are Dudeney type VI.

As already mentioned in "A New Census of Fourth-Order Magic Squares," Dudeney overlooked the partially pandiagonal characteristics, and mistakenly classified these squares as "simple."

Complementary number patterns of the partially pandiagonal tori type T4.03.2

The 12 partially pandiagonal tori type T4.03.2 are here represented by the partially pandiagonal torus with index n° T4.195 (torus type n° T4.03.2.06). This partially pandiagonal torus displays 4 partially pandiagonal squares with Frénicle index n°s 208, 525, 526 and 693. Half of these squares, (including the Frénicle index n° 693 illustrated here), show complementary number patterns that are Dudeney type VII. The other half, (including the Frénicle index n° 208 illustrated here), show complementary number patterns that are Dudeney type IX.

As already mentioned in "A New Census of Fourth-Order Magic Squares," Dudeney overlooked the partially pandiagonal characteristics, and mistakenly classified these squares as "simple."

Complementary number patterns of the partially pandiagonal tori type T4.03.3

The 2 partially pandiagonal tori type T4.03.3 are here represented by the partially pandiagonal torus with index n° T4.217 (torus type n° T4.03.3.1). This partially pandiagonal torus displays 4 partially pandiagonal squares with Frénicle index n°s 181, 374, 484 and 643. All of these squares, (including the Frénicle index n°s 484 and 643 illustrated here), show complementary number patterns that are Dudeney type XI.

As already mentioned in "A New Census of Fourth-Order Magic Squares," Dudeney overlooked the partially pandiagonal characteristics, and mistakenly classified these squares as "simple."

Complementary number patterns of the partially pandiagonal tori type T4.04

The 4 partially pandiagonal tori type T4.04 are here represented by the partially pandiagonal torus with index n° T4.096 (torus type n° T4.04.1). This partially pandiagonal torus displays 2 partially pandiagonal squares with Frénicle index n°s 40 and 522. The square with Frénicle index n° 40 (illustrated here) shows a complementary number pattern that is Dudeney type VIII, whilst the other square with Frénicle index n° 522 (illustrated here) shows a complementary number pattern that is Dudeney type X.

As already mentioned in "A New Census of Fourth-Order Magic Squares," Dudeney overlooked the partially pandiagonal characteristics, and mistakenly classified these squares as "simple."

Complementary number patterns of the basic magic tori type T4.05.1

The 92 basic magic tori type T4.05.1 are here represented by the basic magic torus with index n° T4.002 (torus type n° T4.05.1.01). This basic magic torus displays 2 basic magic squares with Frénicle index n°s 1 and 458. Both of these squares, illustrated here, show complementary number patterns that are Dudeney type VI.

Complementary number patterns of the basic magic tori type T4.05.2

The 32 basic magic tori type T4.05.2 are here represented by the basic magic torus with index n° T4.049 (torus type n° T4.05.2.01). This basic magic torus displays 2 basic magic squares with Frénicle index n°s 23 and 767. The square with Frénicle index n° 767 (illustrated here) shows a complementary number pattern that is Dudeney type VII, whilst the square with Frénicle index n° 23 (illustrated here) shows a complementary number pattern that is Dudeney type IX.

Complementary number patterns of the basic magic tori type T4.05.3

The 4 basic magic tori type T4.05.3 are here represented by the basic magic torus with index n° T4.005 (torus type n° T4.05.3.1). This basic magic torus displays 2 basic magic squares with Frénicle index n°s 3 and 613. Both of these squares, illustrated here, show complementary number patterns that are Dudeney type XII.

Complementary number patterns of the basic magic tori type T4.05.4

The 52 basic magic tori type T4.05.4 are here represented by the basic magic torus with index n° T4.019 (torus type n° T4.05.4.1). This basic magic torus displays 2 basic magic squares with Frénicle index n°s 8 and 343. The square with Frénicle index n° 8 (illustrated here) shows a complementary number pattern that is Dudeney type VIII, whilst the square with Frénicle index n° 343 (illustrated here) shows a complementary number pattern that is Dudeney type X.

Conclusions

We can see that the Dudeney pattern types I, V, XI, and XII are not only valid for magic squares, but also for the magic tori that display these squares. On the other hand, the Dudeney pattern types II and III are shown to be partial viewpoints of a single pattern on the fourth-order magic tori. Again, the Dudeney pattern types IV and VI, the Dudeney pattern types VII and IX, and also the Dudeney pattern types VIII and X, are shown to be partial viewpoints of single patterns on the fourth-order magic tori.

We also notice that some of the detected complementary number patterns have contrasting hemitorus arrangements.

It is necessary to adapt the Dudeney pattern types, and add new symbols that not only reveal the real nature of the complementary number relationships, but also facilitate their comprehension. With this in mind, the 8 figures that follow have been selected to illustrate the essentially different complementary number pattern types that occur on fourth-order magic tori:

To be read with a previous table that compared the 12 Dudeney pattern types with the 12 Magic torus types, published in "A New Census of Fourth-Order Magic Squares," the new table that follows, recapitulates the latest findings, and shows the repartition of the 8 complementary number patterns on the magic squares of the fourth-order magic tori:

Further Developments

New articles entitled "Self-Complementary and Paired Complementary Magic Tori of Order-4" and "Multiplicative Magic Tori" now extend the above findings.

Read more ...

Magic Diagonal Sequences of 4th-Order Magic Tori

The number of fourth-order magic series is 86. The complete list of these magic series has been published by Walter Trump, who gave me confirmation that all of these magic series were present on fourth-order magic squares, even if the geometrical arrangement of the series was often chaotic. He pointed out that for example the series 7+8+9+10 does not exist in any row, column, or main diagonal of a magic 4x4-square, even when considering all the 24 possible permutations of the four numbers. However the series 7+8+9+10 occurs in the 2x2 centre square or in the four corners of certain 4x4 magic squares. As defined in MathWorld , or in Wikipedia, a magic series is not a specific sequence of numbers, but a set of numbers that add up to the magic constant.

The magic constant (MCn) of an nth order magic square (or torus) can be calculated:

MCn = (n²)² + n²  x  1    =    n(n² + 1)

                 2             n               2

For a fourth-order magic square (or magic torus) the magic constant is therefore:

MC4   =  4(4² + 1)    =   34

                    2

Magic diagonal sequences on fourth-order magic tori

Magic diagonal sequences on the Magic Torus Type T4.01.1 (index n° T4.194)

On any magic diagonal of a fourth-order magic torus (or of an order 4 magic square) :

a + b + c + d = 34

Considering the continuous curved surface of a magic torus, each of the 86 4th-order magic series can be expressed in 3 essentially different sequences:

a, b, c, d  (sequence type A) - which is also the magic series

a, b, d, c  (sequence type B)

a, c, b, d  (sequence type C)

As they curve round the torus the sequences have no beginning or end. The magic torus concept is explained in an earlier article "From the Magic Square to the Magic Torus." The interrelationships of the 4th-order magic tori, first explored in the "Fourth-Order Magic Torus Chart," are now more extensively detailed in "Multiplicative Magic Tori."

Theoretically the total number of different magic diagonal sequences on fourth-order magic tori would be 86 magic series x 3 sequence types = 258. However, after checking the 255 different fourth-order magic tori I discovered that there are 48 exceptions, leaving only 210 essentially different diagonal magic sequences. My observations have enabled me to determine some of the rules that govern fourth-order magic diagonal sequences:

Rules for magic diagonal sequences on fourth-order magic tori

Rule 1: If the magic series a + b + c + d has complementary pairs a + d = 17 and b + c = 17 (whatever the order of the sequence), and if consecutive numbers with an even successor number occur, then the series cannot be magic along diagonals.

Rule 2: If the magic series a + b + c + d has complementary pairs a + d = 17 and b + c = 17 (whatever the order of the sequence), and if a and b are odd numbers, then (c + d) - (a + b ) must be a multiple of 3.

Rule 3: If the magic series a + b + c + d has complementary pairs a + d = 17 and b + c = 17 (whatever the order of the sequence), and if a and b are even numbers, then (c + d) - (a + b) must be a multiple of 7.

Rule 4: If the magic series a + b + c + d has complementary pairs a + d = 17 and b + c = 17 (whatever the order of the sequence), and if a - 1 = 8 - b = c - 9 = 16 - d, then the series cannot be magic along diagonals.

Presentation of the list of magic sequences

In the list that follows the index numbers of the magic series are the same as those already published by Walter Trump. I have just added the suffixes A, B, and C to identify the 3 essentially different sequences that are derived from each series. I wish to emphasise that although I have always chosen the lowest number to be the first, none of the sequences have either a beginning or an end, as they each form a continuous loop round their torus.

It was difficult to decide how to present the results. I have chosen to list the different sequence types A, B, and C separately, and I have grouped the sequences by sets of number rhythms in order to facilitate comparisons and reveal patterns. I have also sorted between the complementary (a+d = b+c = n²+1) sequences and the non-complementary (a+d ≠ b+c) sequences.

Please note that if you click on the button that appears at the top right hand side of the pdf viewer below, a new window will open and full size pages of "Magic Diagonal Sequences of Fourth-Order Magic Tori" will then be displayed, with options for zooming.

Observations

Please note that all of the torus diagonals that sum to the magic constant are taken into account - even those that never coincide with the centre of a traditional magic square - such as for example the third magic diagonal sequence (4, 6, 16, 8) of the Frénicle square n° 275 (magic torus type n°T4.04.2 - index n°T4.098).

The complementary (a + d = c + b = n² + 1) diagonal series seem quite symmetrical and regular when compared to their orthogonal and sub-magic 2x2 square cousins. I have therefore decided to use larger sets of complementary sequences in this present study.

However there are many other ways of ordering the sequences to accord with the specific number rhythms of the different magic torus types. This is why an ideal list, that will suit all the torus types, remains a difficult objective.

Read more ...

1,920 Sub-Magic Squares on 255 4th-Order Magic Tori

Further to my last article (published on the 26th March) Harry White has kindly run a computer programme to verify and validate my hypothesis: The 4th-order magic tori are indeed totally covered by sub-magic 2x2 squares.

As Harry White's results gave 7,712 sub-squares for the 880 Frénicle squares it was necessary to determine which tori had a reduced cover of sub-magic squares. After verification I have found that there are two families of the type 2 and type 5 tori. My latest results and totals are given below. It could be that by using observation and manual input I have overlooked something. Your comments are always welcome.

4th-order panmagic or pandiagonal torus type 4.01

4th-order panmagic or pandiagonal torus type 4.01
represented by Frénicle index 102, Dudeney type I

4th-order panmagic or pandiagonal torus type 4.01
represented by 16 sub-magic 2x2 squares

4th-order semi-panmagic or semi-pandiagonal torus type 4.02.1

4th-order semi-panmagic or semi-pandiagonal torus type 4.02.1
represented by Frénicle index 016, Dudeney type VI

4th-order panmagic or pandiagonal torus type 4.02.1
represented by 12 sub-magic 2x2 squares

4th-order semi-panmagic or semi-pandiagonal torus type 4.02.2

4th-order semi-panmagic or semi-pandiagonal torus type 4.02.2
represented by Frénicle index 021, Dudeney type II

4th-order semi-panmagic or semi-pandiagonal torus type 4.02.2
represented by 8 sub-magic 2x2 squares

4th-order partially panmagic or partially pandiagonal torus type 4.03

4th-order partially panmagic or partially pandiagonal torus type 4.03
represented by Frénicle index 046, Dudeney type VI "Simple"

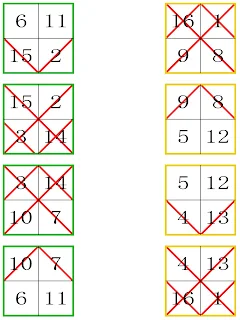4th-order partially panmagic or partially pandiagonal torus type 4.03
represented by 8 sub-magic 2x2 squares

4th-order partially panmagic or partially pandiagonal torus type 4.04

4th-order partially panmagic or partially pandiagonal torus type 4.04
represented by Frénicle index 040, Dudeney type VIII "Simple"

4th-order partially panmagic or partially pandiagonal torus type 4.04
represented by 4 sub-magic 2x2 squares

4th-order basic magic torus type 4.05.1

4th-order basic magic torus type 4.05.1
represented by Frénicle index 002, Dudeney type VI Simple

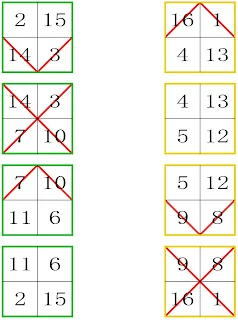4th-order basic magic torus type 4.05.1
represented by 8 sub-magic 2x2 squares

4th-order basic magic torus type 4.05.2

4th-order basic magic torus type 4.05.2
represented by Frénicle index 003, Dudeney type XII Simple

4th-order basic magic torus type 4.05.2
represented by 4 sub-magic 2x2 squares

Please note that the type number of this torus is no longer T4.05.2 but now T4.05.3

Conclusion:

Each number of a fourth-order magic torus (or magic square) comes from at least one 2x2 sub-magic square. Or, expressed otherwise, the surface of every fourth-order magic torus is entirely covered by 2x2 sub-magic squares. This hypothesis has since been confirmed by Harry White's computer skills (see above).

Please note that I have published a new article that extends the above findings.

The table below is a new résumé of the different 4th-order magic tori taking into account the different arrangements of the sub-magic 2x2 squares that cover them.

Read more ...

Sub-Magic 2x2 Squares on Fourth-Order Magic Tori

My recent studies have shown that 2x2 sub-magic squares are fundamental in the way the fourth-order magic tori work.

It has long been known that fourth-order magic squares have 2x2 sub-magic squares at their centres and that the 4 corner numbers of the squares also add up to 34. However, once considered as magic tori, the 4 corner numbers of each 4th-order magic square are in fact another sub-magic 2x2 square, and more subsquares are to be found overlapping the former boundary of the initial square.

I have therefore tried to determine the number of magic sub-magic squares that are displayed on each type of the fourth-order magic tori, and my first results are illustrated below. Using simple observation and manual input I have not verified all of the 880 Frénicle fourth-order squares and may have missed something. Your comments and corrections are welcome.

Surprisingly the fourth-order type 4 partially panmagic torus displays less sub-magic 2x2 squares than the basic fourth-order type 5 magic torus.

Hypothesis

Each number of a fourth-order magic torus (or magic square) comes from at least one 2x2 sub-magic square. Or, expressed otherwise, the surface of every fourth-order magic torus is entirely covered by 2x2 sub-magic squares.

Conclusion

The above remained to be verified by a computer programme until the day after this article was published when Harry White very kindly checked and validated the hypothesis: His results confirm that every 4th-order magic torus (or magic square) is entirely covered by 2x2 sub-magic squares. For all the 880 Frénicle squares he has found 7,712 sub-squares and has confirmed that all the numbers of the different magic squares come from at least one 2x2 sub-magic square.

Harry White's results show that within a same type of tori the patterns and numbers of sub-squares can vary. For example, some of the type 5 tori have a reduced cover of 4 sub-magic squares instead of the 8 subsquares shown above (for example the Frénicle square index 277). This will need to be investigated further.

Please note that I have just published (the 28th March 2013) a new article that takes into account the different arrangements of the sub-magic 2x2 squares, and which attempts to complete the picture.

As for 4th-order semi-magic squares I have started to look into the question and have discovered some examples which are totally covered by 4 2x2 sub-magic squares whilst other examples have no subsquares at all: The phenomenon is not just limited to the magic tori.

Read more ...