Albrecht Dürer's "Melencolia I" contains numerous mathematical and philosophical symbols amongst which we can see a magic square, a polyhedron and a sphere. These 3 symbols are partially interpreted in an earlier article written in French.
1514, the date of the engraving, appears in the lower line of the fourth-order magic square. 500 years later, is it possible to create a fourth-order magic torus tribute to Dürer?
In order to write 2014 we can subtract 1 from all the numbers (1 to 16), and thus obtain the zero that cannot be found in normal fourth-order magic squares. After the subtraction, we can use a flattened viewpoint of the basic magic torus T4.177 (group number T4.05.4.12) that displays not only the Frénicle squares n°99 and 618, but also 14 semi-magic squares. The numbers 0 to 15 are repeated beyond the edges of the square in order to represent the toroidal continuity. As the new figures contain the numbers from 0 to (N²-1) instead of 1 to N², their magic constant is 30 instead of 34.
 |
| A magic torus tribute to Dürer |
 |
| Detail of the "first state" version of the magic square that appears on Dürer's "Melencolia I" (National Gallery of Victoria) |
Perhaps Dürer hesitated when engraving the left hand side of his square: The number 5 appears to replace a former number 6. It should also be noted that the print detailed in the first version above is, according to The National Gallery of Victoria is "the very rare first state." The reversed number 9 was later corrected in the revised version below. On page 12 of the 1961 Aukland City Art Gallery catalogue "Albrecht DÜRER forty engravings and woodcuts," it is written that "There are two states - the first where the nine on the numerical table is reversed, the second where the nine is corrected." The contemplation of the two versions of Dürer's magic square may well remind the reader of the duality of the “De Umbrarum Regis Novum Portis” engravings in Roman Polanski's film "The Ninth Gate." David Fritz Finkelstein has written that "Dürer's engraving MELENCOLIA I was circulated in two versions not previously distinguished. Besides their conspicuous early Renaissance scientific instruments and tools, they contain numerous apparently unreported concealments whose detection reveals heresies expressed in the work." Frickelstein believes that the second version of the engraving is the one in which the number 9 is reversed, and suggests that the numerals 9, 6, and 0 are curled serpents. To find out more please consult Finkelstein's "Melencolia I.1*"
.jpg) |
| Detail of the revised version of the magic square that appears on "Melencolia I" Albrecht Dürer [Public domain], via Wikimedia Commons |
Dürer's square, (Frénicle n° 175), is one of 8 semi-pandiagonal squares displayed by the semi-pandiagonal torus T4.077 (torus type n° T4.02.2.03). The seven other semi-pandiagonal squares that are displayed by the same "Dürer torus" are the Frénicle index n° 27, 233, 360, 421, 583, 803, and 850. The semi-pandiagonal "Dürer torus" T4.077 also displays 8 semi-magic squares, and is completely covered by 8 sub-magic squares. More details of the fourth-order magic tori can be found in earlier articles such as:
"255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus," "Table of Fourth-Order Magic Tori," and "Fourth-Order Magic Torus Chart." Please note that since the 21st January 2018 "Fourth-Order Magic Torus Chart" has now been superseded by "Multiplicative Magic Tori."
 |
| A magic torus tribute to Dürer |
Miguel Angel Amela has very kindly authorised me to publish an extraordinary pandiagonal square he created for this anniversary. Again, this is not a normal 4x4 square, as the magic constant of all the columns, rows, and diagonals is not 34, but 1514 - the year that Dürer engraved Melencolia I! Miguel has also managed to write 2014 at the centre of the bottom row, in just the same cells that Dürer used to date his square.
 |
| Miguel Amela's tribute to Dürer : 2014 - 1514 = 500 years. |
The following figure shows a water retention diagram of Miguel Amela's square that was created by Craig Knecht.
 |
| A water retention diagram of Miguel Angel Amela's tribute to Dürer - diagram by Craig Knecht |
Craig Knecht had already devised a 14 x 14 magic square in 2013 to honour the 500th anniversary of Durer's famous "Melencolia I" magic square. The animation of this water retention square can be found at the following link.
Further to the first edition of the present article, on the 21st May 2015, Miguel Angel Amela sent me this very original magic square that he created to celebrate the 544th birthday of Albrecht Dürer (1471-1528):
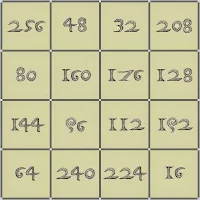 |
| Miguel Angel Amela's 544th birthday tribute to Albrecht Dürer, created on 21st May 2015 |
This is not a normal 4 x 4 magic square as the magic constant of all the columns, rows, and magic diagonals is not 34, but 544. Miguel Angel Amela's creation (using the reversed nine version of Dürer's writing style) is the product of the Dürer square integers and 16 (which is the number of integers). Miguel Angel Amela points out that the divisors of 544 are: 1, 2, 4, 8, 16, 17, 32, 34, 68, 136, 272, and 544:
1, 2, 4, 8, and 16 all figure on Dürer's fourth-order magic square.
17 is the total of the complementary numbers 1 and 16, 2 and 15, 3 and 14, etc. on Dürer's square.
32 is either the product of 4 and 2 times 4, or it is twice the number of the integers on Dürer's square.
34 is the magic constant of Dürer's square.
68 is twice the magic constant (2 x 34) of Dürer's square.
136 is 4 times the magic constant (4 x 34), and therefore the total of all the numbers on Dürer's square.
272 is 8 times the magic constant (8 x 34) of Dürer's square.
544 is 16 times the magic constant (16 x 34) of Dürer's square.
The square includes the numbers 16 (4 to the power of 2), 64 (4 to the power of 3) and 256 (4 to the power of 4) in its corners, and 4x4 magic square enthusiasts will appreciate this subtle wink! Thank you Miguel for allowing me to publish your very original creation!
Lorenzo D. Sisican, Jr.has kindly authorised me to publish two non-normal, but semi-pandiagonal squares that he has created: The first of these squares has a magic constant of 500 in its rows, columns and alternate diagonals (500 years after Melencolia I).
 |
| Lorenzo D. Sisican Jr.'s first tribute to Dürer, 500 years after Melencolia I |
The second of Lorenzo D. Sisican Jr.'s squares is also semi-pandiagonal, and has a magic constant of 500 in its rows, columns and alternate diagonals (500 years after Melencolia I).
 |
| Lorenzo D. Sisican Jr.'s second tribute to Dürer, 500 years after Melencolia I |
The date of the creation of Melencolia I, the year 1514, is obtained by the numbers 151 & 4. The anniversary year 2014 is obtained by the numbers 201 & 4. Melencolia I was created 14 years before Dürer’s death, and the number 14 is also prominent on this square.

Some interesting background history on Magic Squares in art, science and culture on this blog: www.glennwestmore.com.au
ReplyDeletei would like to know why if Durer's magic square has the year at the bottom and hi initials square with 4 and 1 in them respectively why did he not just swap collumns
ReplyDeleteoriginal Durer
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
modified durer with switched columns initials of Albrecht Durer in correct honorable sequence. the switch make the Square no more and no less magic than the square in Melencolia I
13 3 2 16
8 10 11 5
12 6 7 9
1 15 14 4
In Wikipedia , it is stated that “the numbers 1 and 4 at either side of the date correspond respectively to the letters "A" and "D," which are the initials of the artist.”
Deletehttps://en.wikipedia.org/wiki/Magic_square#Albrecht_Dürer's_magic_square
However, as no sources are quoted in Wikipedia, your observation tends to challenge this hypothesis…
All we know for sure is that Albrecht Dürer used several different monograms to sign his works, and that most of these show the “D” or “d” within the “A.” The vertical alignment of his two initials could be interpreted as the wish of the artist to give them an equal emphasis, with no preference for their order. But as it always encompassed the “D” or the “d” in the vertically aligned monograms, the “A” inevitably dominated. Also, for his early drawings prior to 1495, Dürer usually signed with an uppercase “A” in front of a lowercase “d.”
“The Holy Family with the Dragonfly” (circa 1495) is the first engraving on which Dürer placed his monogram.
https://wikivisually.com/wiki/The_Holy_Family_with_the_Dragonfly
One might also wonder why Dürer needed to doubly sign Melencolia I when his single monogram would suffice. If Dürer did not choose the alternative magic square that you suggest, it is probably because he only meant to emphasise the date of his creation.
You have made a good point, and I wish to thank you for your contribution.
For Rob Sellars at https://sketchportraitstudio.wordpress.com/category/gallery-blog/ : As your previous comment as "unknown" on 16/08/2021 was with a profile not recognised by Blogger and giving 404 errors, I am taking the liberty of removing it, but reproducing it in full below:
Delete"It is pure co-incidence that the numbers 15 and 14 appear to represent the year when the picture was made. As you rightly point out, there is Durers normal monogram located elsewhere in the picture that give us the date that the artist completed the work. All of the other numbers in this square have an entirely different meaning since in their original form, as shown in Agrippas diagram of the Jewish Kabbala of the 9 chambers, they are shown in there ancient form representing the Planet Jupiter. Durer manipulates these numbers further for his own reasons but definitely not to tell us the date again! His exact number manipulation must be read within the wider context of his picture narrative and even the trilogy of masterpieces that this picture was a part of.Also, the change in appearance of the number 9 in both versions is not that dissimilar from each other that you could say it had been corrected to a true latin figure 9. More like it still is reversed but represents a different mathematical symbol than the first print. This could more properly relate to the narrative of the picture and reflects what we "see" rather than what we think we should be seeing. More at https://sketchportraitstudio.wordpress.com/2020/08/28/hitlers-favourite-artist-was-a-crypto-jew/"
Thank you for your interesting comments. I am not familiar with the Jewish Kabala of the 9 chambers that you state is shown in its ancient form in Agrippa's 4x4 "Jupiter" magic square. But I do see what you mean by the similarities between Agrippa's "Jupiter" https://carresmagiques.blogspot.com/2020/04/les-carres-magiques-et-les-spheres-1.html and Dürer's "Melencolia I" magic squares, although such transformations by permutations are very common amongst the 880 magic squares of order-4 https://carresmagiques.blogspot.com/2020/04/list-of-880-Frenicle-magic-squares-of-order-4.html.
ReplyDeleteHowever, the interpretation that you have developed in the different pages of your blog is original, and merits further investigation by those who are interested in Jewish symbolism. I have previously seen the Crypto-Jew theory proposed in Elizabeth Garner's blog https://www.albrechtdurerblog.com/category/discovering-the-durer-cipher/, but was unconvinced by her presentation which seemed exaggerated, if not entirely fanciful! In comparison, your pages look much better, with an approach that is not just based on symbols, but also mathematics.
Thank you William, you and your readers may appreciate the following few paragraphs that focus on the date specifically and summarize its significance in the Jewish context to save reading through my full blog (unless this summary arouses more interest that is!)
ReplyDeleteWhy the magic square is included in this picture by Durer.
The primary reason for including a magic square at all in this picture is that they were uniquely part of Jewish ancient culture (but not well known outside of this sphere) and along with their mathematical/astronomical connotations the numbers/ letters were adjusted to provide talismans for various good luck charms by Jewish apothecarys. Durer has adjusted the one we see on this picture, the question is therefore how does this affect its meaning? Use of the original magic square would not be significant of Jews in itself but the change in the number sequence to produce a talismanic meaning immediately labels it as a Jewish construct that dates back even further, possibly to Chaldean times in the Levant. Talismans were normally quite personal and usually worn hidden in some piece of clothing or under some secret hidden place in order for their “charms” or “spirits” to work against evil. For Christians these types of Magic squares would have been very new and rare for the common people to have seen, the printing press had only been invented just 20yrs before and the publication of Agrippa`s Book on Occult Philosophy (which detailed their use) was not widely distributed & also a very recent publication so only a Jewish person would recognise the "adjusted" square as a Jewish Talisman.
The original meaning of the 34 magic square from ancient times was to represent the God of the Planet Jupiter or even the Planet itself. By using this magic square as opposed to any other Durer is putting a “pointer” on the picture that says Jupiter. Jupiter was the chief God of the Roman Pantheon but probably only the Jewish people would associate this with the Romans who destroyed the Jews Prized Temple of Solomon in Jerusalem in 70CE, their only Temple in the world and the place where God was said to reside inside the Holy of Hollies. Not only did the Romans destroy their Temple and ban them from their Holy city of Jerusalem, they also built their own Temple to Jupiter upon the ruins of Solomons Temple rubbing further indignation into their wounds. Use of this Magic square then would appear to link the Magic Square to the Roman God Jove, the Planet Jupiter, Jerusalem and the destruction of the Temple of Solomon by the Romans in 70CE.
The 2 DATES 1514 (covered in next post due to 4,096 character restriction)
The 2 DATES 1514
ReplyDeleteDurers movement of the Magic squares numbers is most apparent in the switch or move of the two numbers 15 and 14 at the top of the square to their respective “mirror” position at the bottom of the square ( a common Jewish Gematria juxta-position which indicates deeper meaning are to be found in the numbers or letters shown). 1514CE then could also mean the “mirror” date 1514BCE. This was a momentous year in the Jewish Calendar since it was the year that their Patriarch Moses led them out of Egypt on a bright “full-moon” night after the angel of Death had visited the 10th and last of Gods plagues on the Egyptians. This event has been celebrated after sun-down only by Jews ever since as their PASSOVER feast and was marked on the original night by making angular blood lines on the exterior opening side of their door lintels and uprights with the blood of a lamb or goat so that the Angel of Death would spare their first born sons. These marks were called MEZUZAH and are named in the book written by Moses himself, called in Greek the Book of Exodus (or as the Jewish call it, the book of names/numbers). Ever since then, Passover can only be celebrated on a Full moon if you are a Jew, the first full moon after the vernal equinox of 21st March each year, further confirming the significance of the Moon to the Jewish calendar and religion. This was a point of major schism between early Christian or Christian Jews and Jews as the Christians and Christian Jews celebrated this according to their solar calendar in the day-time as opposed to the Jews who celebrated it in the evening of the full-moon. This gives a strong motivation for the number mirroring by Durer and the inclusion of the “moonbow” in the picture because it highlights this particular date, event and point of differentiation between a Jewish person and a Christian, it would not be significant to any one who was not Jewish.
The LUNAR/JEWISH connection
Another obvious reference to the Passover feast are the 4 nails on the floor of the picture, the messianic lamb/dog, the angels of judgement next to the scales of judgement and the number 34, according to the Bible, Jesus was 33/34 at the time of his crucifixion and was hurriedly taken down off the cross to get his body into a Tomb because the Jewish Passover feast was due to start that very evening! This is another pointer to the Lunar aspect of the Jewish feast, it also gives another Jewish Lunar numeric significance to the number 34 in that it is the first year after the 33yr Lunar cycles where Sun and Moon all synchronise. Interestingly the mirror number of 34 is 43 which is the exact angle of elevation from the horizon at which the Lunar “moonbow” becomes invisible to the viewer. The phenomena of a Lunar “moonbow” is quite rare and can only be viewed when the Moon is behind the viewer, upto 42 degrees elevation, near a water feature and when the Sun is not present (just after dusk and just before dawn), so Durer has given a lot of information to us by cleverly concealing the actual Moon itself. It is a very deliberate pointer to the importance of the Moon in this composition and trio of masterpieces.
(one more para to go!)
The date reference to the PASSOVER feast combined with the mirroring effect of the date itself would immediately bring a Jewish persons attention to Moses and the events of the Book of Exodus, their 40 years wanderings in the desert to the south of their promised land and Jerusalem. The Book they called the book of Names and Numbers (their letters having the dual use of representing both verbal and mathematical values). Only a Jewish person would now look for greater meaning from within the numbers and letters of this square, finding them in the first instance with the Magic Squares number of 34 as this chapter is arguably the most important chapter of Moses Book of Exodus/Names/Numbers because it details the Sinaitic Covenant between Moses and God on behalf of the Jewish people. It is the very foundation of the Jewish religion and details how God will live amongst them in the Holy of Hollies and how they should build the Tabernacle that will house the Holy of Hollies. Initially this is a tent based structure that later acts as the Blue-Print for Solomons Temple (the Temple of the Sun and Moon and that later became the “nickname” for the son of King David who actually built it). It gives the exact dimensions, usage of the various areas of the construction and even the materials to be used. Therefore this chapter 34 brings us back again to the Temple of Solomon, it is the first time God tells Moses his ineffable name YHVH(3 vowels and 4 consonants) and that it should be carved upon the cubic stone altar of the Tabernacle where he will dwell inside the Ark of the Covenant , it details the written and oral commandments and the laws of God, his benifices and his wraths (also detailed as multiples of 3 and 4 in the text). This chapter reference is a “pointer” to the terms of the Siniatic Covenant which should turn a Jewish viewers attention straight to the flying beast underneath the Lunar “moonbow” in the picture which is again a clear reference to an event that was part of the Siniatic Covenant and it is the only item in the picture that is displaying a name on it, indicating that its identity would be found in the Book of Exodus/Names/Numbers.
ReplyDeleteThe FLYING CHIMERA
During the 40yrs wanderings in the Deserts, God gave the Jews a list of Laws and Kosher items that they were allowed to eat and items that they were forbidden to eat as his Holy People (later this became another point of schism between early Christians and Jews in the same way that the calendrical differences had). On that list was a particular Egyptian water fowl or mole whose name has often caused confusion during Greek/Hebrew translations. The Jewish knew it as TINSHEMETH and it occurs only 2 times in Moses Books- once in Genesis and once in Leviticus so its easy for us to track down and deduce its meaning. The fact that Durer combines the Tinshemeth features of the flying water-fowl and the earth mole (with which its name was often confused) into the same animal as a chimera and the fact that it is referenced by the Book of Exodus/Names/Numbers is the clue that the name it has exposed “Melancholia I” is an anagram or jumbled-up version of the animals names letters and/or numbers. The anagram “MELENCHOLIA I “ decrypts to Chamelion in Latin but which in Greek( the language used by Ptolemaic Egyptian translators of the Septuagint Bible) would be more correctly written CHAMEILEON (leaving an L and the I to resolve completely). The L and I have number values in the Jewish language which correspond to 10 and 30 which when added together produce the number 40 = the 40yrs wanderings in the desert and the time period from where the origin of this rule came from i.e The Exodus 40yrs.
At this point there would be no doubt in a Jewish persons mind about the symbology of this picture and the deeper meanings that could be found if he had the eyes to look. At the top of his list now would be the stone and the Angels sitting near to it. How does it tie-in to the deeper meanings of the picture?
The Durer Stone
ReplyDeleteThe most famous stone in Jewish history is the Cubic Altar stone carved with the ineffable name of God that disappeared at some time from the Temple of Solomon. But this stone is anything except cubic, so where is the clue to its meaning? This takes you back to the 4x4 Magic square that we have already seen references the ineffable name of God and is at least square in shape (a 2D cube). Mathematically the square has 4 x 4 numbers =16 and each number is unique from 1-16 and therefore only 12 numbers can correspond to the 12 vertices on the Durer stone. Its not easy to find the shape hidden within the stone and it can only translate into the symbols, numbers and letters that are shown on my website and I am sure that it would have to have been explained to someone that it was there BUT that is the true genius of it.
The resultant mapping of the vertices leads to the 2 triangles forming the star of David and the Hexagonal shape surrounded by the circle representing the astronomical significance of the Jewish heritage and key point of differentiation between them and other religions. The 12 points of the star of David can be used to symbolise the 12 different tribes of Israel or the astronomical points of their Lunar/Sun zodiac star constellations in the night sky, crucial for managing any time calculation or spatial positioning (trigonometry). The 5 pointed Pentagon of Venus is easily produced from this and is the body which synchronises most readily with the Sun and the Moons cycles. This is the Triumvirate when viewed from earth and the 3 heavenly bodies that were of prime concern to the Jewish people. Durer confirms this by mapping 6 ( 2 x 3 ) specific letters/numbers to a coded message that can only be read in Jewish Gematria or as numbers with Astronomical significance.
The letters form 2 Jewish words which identify with the ancient city of Jericho (literally means city of the moon) and the large watchtower (or moon observatory) located within the city. Jericho was the first city that the Israelites conquered in the promised land with Gods help and of major significance to the Jews History as it is chronicled in the Books of Moses as a great victory. Together these 2 words leave no doubt about who or what the purpose of the picture is for. The numbers are of deeper astronomical significance and relate to the earths precessional wobble 1/9 of a degree every 8yrs (or 1 degree every 72yrs), the moons ecliptic angle of 5.15 degrees and Venus synchronisation with both of these bodies and its ecliptic angle of 3.4 degrees.
There is so much more to this that then relates to the other pictures, for example the miss- engravings of certain numbers etc and ties them in as a true TRILOGY but this summary is concerned mainly with the immediate visual Jewish symbology of the Melancholia I picture.
Reply 1.1:
ReplyDeleteMany thanks Rob, for your 4 new comments dated 10th September 2021, which follow your first post signed “Unknown” on the 16th August 2021. I think that since reading my first reply dated 25th August 2021 you will have realised that I am a gentile. I have nothing against religions in general, as long as they remain in the private sphere. However, I do consider that the subject of Dürer's "Melencolia I" and its related magic square, can, alongside the study of other symbols and mathematics, have religious interpretations without necessarily imposing a revealed “truth.”
I hope you won’t mind me reacting to some of your latest comments:
As I am an uninitiated outsider to your religion, I cannot comment on your theories about Dürer conveying an encrypted Jewish message. However, I am surprised to read your claim that magic squares were “uniquely part of Jewish ancient culture” prior to Dürer’s engraving of “Melencolia I.” It is widely accepted that the magic square of order-3 was known to Chinese mathematicians as early as 190 BCE, and that the first datable appearance of an order-4 magic square occurred in India in 587 CE. Circa 983 CE, illustrations of magic squares surfaced in an encyclopaedia from Baghdad, and by the end of the 12th century general methods for constructing magic squares were well known. Magic squares had first been made known to Europe in the “Kitāb tadbīrāt al-kawākib” (the Book on the Influences of the Planets) by the Arab Muslim Ibn Zarkali of Toledo, in the 11th century (work which was then translated into Latin by the Italian translator Gerard of Cremona in the 12th century). Around 1315 CE, the Greek Byzantine scholar Manuel Moschopoulos wrote a treatise on magic squares, and later, in the 14th century, the Florentine mathematician Paolo Dagomari illustrated magic squares of orders 6 and 9 in his Trattato d'Abbaco (Treatise of the Abacus). Meanwhile, magic squares talismans (or occult objects) were being regularly disseminated throughout Europe via Spain and Italy.
Because the character count must not exceed 4096, my reply is continued below...
Reply continued 1.2:
ReplyDeleteSo I cannot believe that Dürer’s magic square was only meant for Jews, or that it could only be properly interpreted by them. Using a Platonic Renaissance intellectual approach, Dürer was clearly aiming at an elite circle when producing “Melencolia I,” and though his mood at that time was probably influenced by the Johannes Reuchlin Affair and by ongoing tensions within the Church, his symbolism does not impose a religious exclusivity. For example, supposing that the central winged person of “Melencolia I” might be an angel, a figure such as this is not only important in Judaism, but also in Christianity, Islam, and in other religions (https://en.wikipedia.org/wiki/List_of_angels_in_theology).
Your theory about the date 1514 CE being a mirror of 1514 BCE (the year of the Jewish calendar in which Moses led the Jews out of Egypt) is new to me. But after verification I see that the exact date of the Exodus is subject to great deal of controversy amongst scholars (as discussed by Walter Reinhold Warttig Mattfeld y de la Torre at http://www.bibleorigins.net/Exodus1540BCHyksos.html). The most commonly proposed dates range between 2670 BCE and 1759 BCE, and there are so many possibilities, that I would exclude the idea that Dürer was thinking about the Exodus when he engraved “Melencolia I.” But during 1514 CE his mother Barbara Holper passed away, or “died hard” as Dürer described it. We can therefore suppose that Dürer’s grief could have been a catalyst, not only of the very melancholic atmosphere depicted in “Melencolia I,” but also of the extra importance given to the date 1514, which he engraved twice.
I have been lucky enough to have actually seen a moonbow for myself, and I still remember its subtle shades that seemed to range from light grey to blue. But when Dürer engraved this phenomenon in his “Melencolia I,” might it not have just been an additional symbol of melancholy? And, as the engraving is intended for monochrome prints, can we really be sure that we are looking at a moonbow, and not a rainbow? I suppose the moonbow makes more sense, because we can see what looks like a comet or a falling star, and also flying bat-like creature.
Because the character count must not exceed 4096, my reply is continued below...
Reply continued 1.3:
ReplyDeleteThe flying Chimera, that you see and interpret as a combination of the Tinshemeth features of the flying water-fowl and the earth mole, looks more like a bat to me, but perhaps I am over-simplifying! I see that other sources identify the Tinshemeth as a bat, chauve-souris in French (Rashi; Chizzkuni). Rashi says it is a nocturnal flying animal that is like a rat, and the Stone (Art Scroll) commentary says that this means it is a bat. (https://judaism.stackexchange.com/questions/57276/what-is-a-tinshemet). Nearly all species of bats have tails, even if most of these are shorter and thinner than the one that Dürer has depicted. But a strange detail that we can see is that the body of the animal appears to be above its wings, which is impossible unless the bat is flying upside-down! More examination reveals that this is not the case, as the mouth and eyes of the beast are those of an animal with an upright head. But Dürer was using his artistic licence in the “Melencolia I” engraving, and it is therefore hardly surprising that his flying beast looks a bit bizarre.
Your reference to Dr Ernst Theodor Mayer’s projection is one of at least five theories concerning the construction of Dürer’s polyhedron. But as Günter M. Ziegler points out in his article “Dürer's polyhedron: 5 theories that explain Melencolia's crazy cube” (in Alex Bellos’s Adventures in Numberland at https://www.theguardian.com/science/alexs-adventures-in-numberland/2014/dec/03/durers-polyhedron-5-theories-that-explain-melencolias-crazy-cube?CMP=share_btn_tw): “there is an extensive tradition of over-interpretation in this context. And indeed, you can easily find 500 interesting lines, circles, ellipses, intersections, patterns and structures in the little copper engraving ... and then interpret! And Herr Mayer is very good at that.”
Your interpretation of “Melencolia I” is still an interesting story, and any other references that could justify the dates, etc. would be of great help to your readers.