Plus or Minus Groups of Magic Tori of Order 4

As the positive integer entries of normal magic tori, and of their displayed magic squares, are always arranged in same-sum orthogonal arrays, it would seem logical to compensate any additions or subtractions to those entries, by making corresponding subtractions or additions. How can we develop this simple observation?

Preliminary Definitions

A normal magic square is an N x N array of same-sum rows, columns and main diagonals. If the magic diagonal condition is not satisfied, the square is deemed to be semi-magic. The torus, upon which a magic or semi-magic square is displayed, can be visualised by joining the opposite edges of the magic or semi-magic square in question.

There are N x N square viewpoints on the surface of a torus of order N. A normal magic torus has N x N arrays of same-sum latitudes and longitudes, and at least one magic intersection of magic diagonals on its surface. In his paper "Conformal Tiling on a Torus" published by Bridges in 2011, John M. Sullivan shows that, on a square torus T1, 0, the diagonal grid lines “form (1, ±1) diagonals on the torus, each of which is a round (Villarceau) circle in space.”

Semi-magic tori can also have magic diagonals, but the latter can never produce the magic intersections required for magic squares, either because the magic diagonals are single or parallel, or because they do not intersect correctly. Additional information about magic and semi-magic tori, with further explanations of their diagonals, can be found in the references at the end of the enclosed paper.

In order 4, starting with any magic torus, and examining cases where half of the torus numbers are subjected to equal additions, and the other half are subjected to same-integer subtractions, we notice the following: From its initial state (which we can call 0), each magic square can be transformed by four plus or minus operations that will either produce alternative magic or semi-magic square viewpoints of the same torus, or square viewpoints of other essentially different magic or semi-magic tori. Here's a simple example of two transformations:

3 Magic Tori of Order 4 linked by by Complete-Torus, Same-Integer, Plus or Minus Operations

Complete-Torus, Same-Integer, Plus or Minus Groups in Order 4

Please note that, in order 4, the orthogonal totals of magic and semi-magic tori are always 34. Therefore, only the diagonal totals, which can vary, are announced here. These totals are interesting because of their symmetries, and in the example illustrated above, there are pairs of diagonals that always sum to 68 (twice the magic sum). Each of the 255 magic tori of order 4 is similarly examined, and the results are given in tables and observations at the end of the following PDF paper: "Groups of Magic Tori of Order 4 Assembled by Complete-Torus, Same-Integer, Plus or Minus Operations"

Complete-Torus, Same-Integer, Plus or Minus Groups in Orders N > 4

The same method cannot always be applied to higher even orders. A quick look at some examples from even orders N = 6, N = 8, and N = 10 shows that certain magic tori have either no solutions whatsoever, or only one that can be used in a complete-torus same-integer plus or minus matrix to produce another orthogonally magic torus. In singly-even orders, even divisors with odd quotients have to be ruled out. Each case will need to be tested, and systematic computer checks will be necessary for these higher even orders.

An adaptation is of course required for odd orders, as their odd square totals do not have even integer divisors. But partial-torus same-integer divisions produce plus or minus solutions, and there are a variety of approaches.

The following paper, entitled "Examples of Partial Groups of Magic Tori of Orders N > 4 Assembled by Complete-Torus (or Near-Complete in Odd Orders) Same-Integer, Plus or Minus Operations" shows how the method used for order 4 gives some good results in higher orders:

New Developments

Since the 9th October 2024, in order to facilitate cross-referencing, the "List of 880 Frénicle Magic Squares of Order 4" (initially published on the 14th September 2019), has been updated with the detail of the Plus or Minus Groups of Magic Tori.

Since the 14th October 2024, in order to facilitate cross-referencing, the paper entitled "137 Plus-or-Minus Groups of Magic Tori of Order 4 listed with the details of the four squares generated by each of the 880 Frénicle magic squares" is available below:

Read more ...

List of the 880 Frénicle Magic Squares of Order-4

Bernard Frénicle de Bessy was the first to determine that there were 880 essentially different magic squares of order-4, and his findings were published posthumously in the "Table Générale des Quarrez Magiques de Quatre," in 1693.

Title of Frénicle's study of magic squares published in 1693

The "Table Générale des Quarrez Magiques de Quatre" published in 1693

It was more than 300 years later, that it was discovered that these 880 magic squares of order-4 were displayed on 255 magic tori of order-4. At first listed by type in 2011, the 255 magic tori of order-4 were later given additional index numbers in a "Table of Fourth-Order Magic Tori" in 2012. In 2019 some of the magic tori of order-4 were found to be extra-magic, with nodal intersections of 4 or more magic lines and / or knight move magic diagonals. Other studies of the magic tori of order-4 have included sub-magic 2 x 2 squares (in 2013), magic torus complementary number patterns (in 2017), and even and odd number patterns (in 2019). Then after a gap of 5 years, the magic tori have been found to belong to 137 plus or minus groups (in 2024).

It has become increasingly important to provide an easily accessible document that recapitulates these different findings. I have therefore compiled the following "List of the 880 Frénicle Indexed Magic Squares of Order-4," with their corresponding Dudeney types and also full details of the magic tori:

Read more ...

Even and Odd Number Patterns on Magic Tori of Orders 3 and 4

Ancient references to the pattern of even and odd numbers of the 3 × 3 magic square appear in the "I Ching" or "Yih King" (Book of Changes). In the introduction to the Chou edition, the scroll of the river Loh or "Loh-Shu", which is represented by the magic square of order-3, is written with black dots (the yin symbol and emblem of earth) for the even numbers, and white dots (the yang symbol and emblem of heaven) for the odd numbers. The "Loh-Shu" is incorporated in the writings of Ts'ai Yuän-Ting who lived from 1135 to 1198:

The Scroll of Loh, according to Ts'ai Yüang-Ting

A normal magic torus (or magic square) of order-n uses consecutive numbers from 1 to n² and consequently, for the order-3, the magic constant (MC) = 15. The Loh-Shu Magic Torus of Order-3 is presented below, together with its corresponding even and odd number pattern P3:

The "Loh-Shu" Magic Torus of Order-3 and its Even and Odd Number (x mod 2) Pattern P3

The magic torus T3 of order-3 is shown here as seen from the Scroll of Loh magic square viewpoint.

The even and odd number pattern P3 has reflection symmetry (with 6 lines of symmetry); rotational symmetry (of order 4); and point symmetry (over number 5, between numbers 3 and 7, between numbers 1 and 9, and between numbers 4, 6, 2, and 8).

The Even and Odd Number Patterns of the Magic Tori of Order-4

Only consecutively numbered magic tori (with numbers from 1 to n²) are studied here, and therefore, for order-4, the magic constant MC = 34.

The "Table of Fourth-Order Magic Tori" lists and describes each magic torus of order-4 using index numbers, while "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus" gives a group categorisation of the magic tori of order-4 using type numbers. Both of these classifications give the details of the Frénicle indexed magic squares that are displayed by each torus.

In the study that follows it can be seen that there are 4 essentially different even and odd number patterns on the magic tori of order-4:

The Order-4 Even and Odd Number Pattern P4.1
(represented by the pandiagonal torus T4.198)

The Pandiagonal Torus T4.198 of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.1

The pandiagonal torus of order-4 (with index n° T4.198 and type n° T4.01.2) is shown here as seen from the Frénicle n° 107 magic square viewpoint.

The even and odd number pattern P4.1 has reflection symmetry (with 6 lines of symmetry); rotational symmetry (of order 2); and multiple point symmetry when reading as a torus. The pattern P4.1 also has negative symmetry (evens to odds and vice versa).

The even and odd number pattern P4.1 concerns 79 out of the 255 magic tori, and 404 out of the 880 magic squares of order-4. These include the 3 pandiagonal tori that display 48 pandiagonal squares; 30 semi-pandiagonal tori that display 240 semi-pandiagonal squares; 12 partially pandiagonal tori that display 48 partially pandiagonal squares; and also 34 basic magic tori that display 68 basic magic squares.

The Order-4 Even and Odd Number Pattern P4.2
(represented by the semi-pandiagonal torus T4.059)

The Semi-Pandiagonal Torus T4.059 of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.2

The semi-pandiagonal torus of order-4 (with index n° T4.059 and type n° T4.02.2.01) is shown here as seen from the Frénicle n° 21 magic square viewpoint.

The even and odd number pattern P4.2 has reflection symmetry (with 8 lines of symmetry); rotational symmetry (of order 4); and multiple point symmetry when reading as a torus. The pattern P4.2 also has negative symmetry (evens to odds and vice versa).

The even and odd number pattern P4.2 concerns 72 out of the 255 magic tori, and 256 out of the 880 magic squares of order-4. These include 18 semi-pandiagonal tori that display 144 semi-pandiagonal squares; 6 partially pandiagonal tori that display 16 partially pandiagonal squares; and also 48 basic magic tori that display 96 basic magic squares.

The Order-4 Even and Odd Number Pattern P4.3
(represented by the partially pandiagonal torus T4.186)

The Partially Pandiagonal Torus T4.186 of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.3

The partially pandiagonal torus (with index n° T4.186 and type n° T4.03.1.3) is shown here as seen from the Frénicle n° 100 magic square viewpoint.

The even and odd number pattern P4.3 has reflection symmetry (with 8 lines of symmetry); rotational symmetry (of order 4); and multiple point symmetry when reading as a torus. The pattern P4.3 also has negative symmetry (evens to odds and vice versa).

The even and odd number pattern P4.3 concerns 16 out of the 255 magic tori, and 44 out of the 880 magic squares of order-4. These include 6 partially pandiagonal tori that display 24 partially pandiagonal squares; and also 10 basic magic tori that display 20 basic magic squares.

The Order-4 Even and Odd Number Pattern P4.4
(represented by the basic magic torus T4.062)

The Basic Magic Torus T4.062 of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.4

The basic magic torus (with index n° T4.062 and type n° T4.05.1.12) is shown here as seen from the Frénicle n° 37 magic square viewpoint.

The even and odd number pattern P4.4 has reflection symmetry (with 8 lines of symmetry); rotational symmetry (of order 2); and multiple point symmetry when reading as a torus. The pattern P4.4 also has negative symmetry (evens to odds and vice versa).

The even and odd number pattern P4.4 concerns 88 out of the 255 magic tori, and 176 out of the 880 magic squares of order-4. All of these 88 magic tori and the displayed 176 magic squares are basic magic.

Observations on the Even and Odd Number Patterns of the Magic Tori and Magic Squares of Order-4

The findings of the even and odd number patterns of the magic tori of order-4 are recapitulated and analysed in comparative tables, (together with the Dudeney complementary number patterns and the Magic Torus self-complementary and paired complementary number patterns), in the file below:

The Even and Odd Number Patterns of the Semi-Magic Tori of Order-4

Only consecutively numbered semi-magic tori (with numbers from 1 to n²) are studied here, and consequently, for the order-4, the magic constant MC = 34.

In "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus" the 4,038 semi-magic tori of order-4 have been sorted, and type numbers have been attributed taking into account the arrangements of their magic diagonals (if any). 

Each of the four even and odd number patterns already found above on the magic tori of order-4, also occur on semi-magic tori of order-4. For example, from left to right below, we find a semi-magic torus type T4.08.0W with pattern P4.1; a semi-magic torus type T4.08.0X with pattern P4.2; a semi-magic torus type T4.07.0Y with pattern P4.3; and a semi-magic torus type T4.09.00Z with pattern P4.4:

Semi-Magic Tori of Order-4 with Even and Odd Number (x mod 2) Patterns P4.1, P4.2, P4.3 and P4.4

The even and odd number patterns P4.1 to P4.4 are not the only ones that can be found, but the patterns which are specific to the semi-magic tori of order-4 have neither been fully investigated nor precisely counted, and the examples that follow only represent some of the different varieties.

The Order-4 Even and Odd Number Pattern P4.5
(represented by the semi-magic torus type T4.06.0A)

The Semi-Magic Torus type T4.06.0A of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.5

This semi-magic torus type n° T4.06.0A was found by Walter Trump, and has been previously illustrated in "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus".

The even and odd number pattern P4.5 has diagonal reflection symmetry (with 4 lines of symmetry); and negative (evens to odds and vice versa) rotational symmetry (of order 2). The blocks of even and odd numbers are translations of each other.

The Order-4 Even and Odd Number Pattern P4.6
(represented by the semi-magic torus type T4.07.0A)

The Semi-Magic Torus type T4.07.0A of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.6

This semi-magic torus type n° T4.07.0A was found by Walter Trump, and has been previously illustrated in "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus".

The even and odd number pattern P4.6 has reflection symmetry (with 4 lines of symmetry); rotational symmetry (of order 2); and multiple point symmetry when reading as a torus. The blocks of even and odd numbers are translations of each other.

The Order-4 Even and Odd Number Pattern P4.7
(represented by the semi-magic torus type T4.09.00M)

The Semi-Magic Torus type T4.09.00M of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.7

This semi-magic torus type n° T4.09.00M was found by Walter Trump, and has been previously illustrated in "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus".

The even and odd number pattern P4.7 has both positive and negative reflection symmetry; negative rotational symmetry (of order 2); and multiple negative point symmetry when reading as a torus. The blocks of even and odd numbers are translations of each other.

The Order-4 Even and Odd Number Pattern P4.8
(represented by the semi-magic torus type T4.10.000X)

The Semi-Magic Torus type T4.10.000X of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.8

3,726 semi-magic tori of the type 10 have been found by Walter Trump, and his findings are detailed in "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus".

The T4.10.000X's even and odd number pattern P4.8 has negative reflection symmetry (2 lines of symmetry); negative rotational symmetry (of order 2); and multiple point symmetry when reading as a torus. The blocks of even and odd numbers are translations of each other.

General Observations

The "Table of Fourth-Order Magic Tori" has been revised to include the even and odd number pattern references for each of the magic tori of order-4 (listed together with the Frénicle indexed magic squares that each magic torus displays).

Other interesting websites that examine, but do not enumerate, the different even and odd number patterns on magic squares of order-4, include "4x4 Magic Squares" by Dan Rhett and "Pattern in Magic Squares" by Vipul Chaskar.

A brief look at higher-orders suggests that the order-5 has many irregular patterns; the order-6 has many patterns with negative reflection symmetry (evens to odds and vice versa); the order-7 has many patterns with rotational symmetry; and the order-8 has patterns very like those of the order-4 examined above. All of these orders merit an in-depth analysis of their even and odd number patterns.

In conclusion, it is interesting to note that the Arab mathematicians of the tenth century constructed odd-order magic squares with striking even and odd number patterns (as for example the magic squares in figures b44 and b49 on pages 243 and 248 of Magic Squares in the Tenth Century: Two Arabic treatises by Anṭākī and Būzjānī, translated by Jacques Sesiano). And in the same context, Paul Michelet has recently brought to my attention a magnificent 15 x 15 magic square by Ali b. Ahmad al-Anṭākī (d. 987). Al-Anṭākī's bordered magic square is solid evidence of the Middle Eastern mathematicians' mastery of even and odd number patterns!

Read more ...

Extra-Magic Tori and Knight Move Magic Diagonals

Published by Carlos Rivera on his website "Prime Puzzles" at the end of May 2019, the Puzzle 391 "9 dots and 8 lines graph" has stimulated a lot of conversation between magic square enthusiasts, and has inspired several ongoing experiments. It has also prompted me to look into the magic line graphs of magic tori, and to search for cases having a maximum number of magic line intersections.

The extra-magic tori of orders 3 and 4 are here presented in detail, together with some further observations on the extra-magic tori of orders 5 to 8, the eighth-order being particularly significant for those who are interested in chess moves...

The Definition of Extra-Magic

Extra-Magic can be defined as the presence of any magic line intersections on Magic Tori that are not usually taken into account in the study of Magic Squares.

For example, the central intersection of the magic diagonals of a magic square takes place between the number cells of even-order magic squares, and over a number cell of odd-order magic squares. When we begin to study the wrap-around characteristics of the magic tori that display the magic squares, we notice that a same pair of magic diagonals produces two intersections on a magic torus. In even-orders the two intersections of a same pair of magic diagonals always produce two distinct magic squares on the magic torus. In odd-orders the two intersections of a same pair of magic diagonals only produce a single magic square, because the second intersection (at the opposite side of the torus), occurs between number cells, and cannot be at the centre of a second magic square.

Therefore, in even-orders, the cases where the intersections of magic diagonals occur over number nodes (2 magic orthogonals + 2 magic diagonals), are often ignored, because these never produce magic squares. However, when looking at the limitless surface of a magic torus, which has no centre, a concentration of magic lines that intersect over a number in even-orders becomes a very interesting feature.

A second example of extra-magic is the presence of knight move magic diagonals that occur on some magic tori (and on the magic squares that the magic tori display). The present study takes into account the eight traditional chess knight moves of (2, 1), (1, 2), (-1, 2), (-2, 1), (-2, -1), (-1, -2), (1, -2) and (2, -1). Other fairy chess "leaper" move magic diagonals also exist, such as the Camel (3, 1) and Zebra (3, 2). However, in order to simplify the graphics of the magic line graphs, only traditional knight moves are considered here. It should be noted that knight move diagonals can never intersect at the centres of even-order magic squares, but they contribute to the weave of magic lines and are always an interesting feature when we observe the limitless surface of magic tori.

Knight Move Magic Diagonals

Because knight move magic diagonals connect n numbers (where n is the order of the magic torus), and one of the knight's steps has a length of 2, the diagonal has to make 2 loops round the magic torus. In lower-n-orders, the reduced number n of the necessary knight moves results in a proximity of the 2 loops, which in turn allows the knight to use 2 magic diagonal paths to connect a same series of numbers! Please refer to "Knight Move Magic Diagonals on Magic Tori" to see why knight move magic diagonals can sometimes have 2 paths for a same series of numbers.

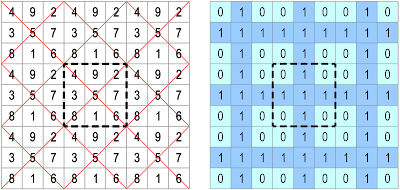
Extra-Magic Torus of Order-3
with 4 Knight Move Magic Diagonals

It came as quite a surprise to find that there are 4 knight move magic diagonals on the traditional Lo Shu magic square!

Lo-Shu Extra-Magic Torus T3 of Order-3

The extra-magic of the knight move diagonals produces multiple intersections of magic lines over the number 5. After the addition of the knight move magic lines that sum up to the magic constant MC = 15, the maximum number of magic lines at a nodal intersection is 8, (at number node 5). The total number of magic lines on the "Lo Shu" Magic Torus T3 is therefore 6 orthogonals (in red) + 2 classic diagonals (in red) + 4 knight move diagonals (in blue) = 12 magic lines.

To the best of my knowledge, the knight move magic diagonals of the Lo Shu have not been mentioned in magic square literature before, but should I be mistaken, can you please advise me, and I will cite any previous authors accordingly. It should be noted that on page 37 of his 1877 paper "On the General Properties of Nasik Squares", Andrew Hollingworth Frost describes (1, 2) "pathlets" of construction for a 3 x 3 square, but his diagram E is not the traditional Lo Shu.

Legend of the Extra-Magic Line Graphs

Legend of the Extra-Magic Line Graphs of Magic and Semi-Magic Tori

Extra-Magic Tori of Order-4 

More details of the Magic Tori of Order-4 (and of the Frénicle indexed squares that these tori display) can be found in "The Table of Fourth-Order Magic Tori" (revised on the 20th June 2019 to include the details of the Extra-Magic Tori), and in "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus". 

The total numbers of Extra-Magic Tori (with extra-magic intersections and / or knight move magic diagonals), that were previously given at the end of the "The Table of Fourth-Order Magic Tori", remain unchanged. Those concerning uniquely the knight move magic diagonals are now listed for more convenient reference in "Knight Move Magic Diagonals in Magic Tori and Magic Squares of Order-4". Miguel Angel Amela has since confirmed my findings although we have a slightly different approach to the count of the double-slanting same-series knight move magic diagonals. For the sake of symmetry, and for comparison with higher-orders, I have chosen to count both of the same-series slants of knight move magic diagonals for the orders-n where n < 6.

Only consecutively numbered magic tori (with numbers from 1 to n²) are studied here, and consequently, for order-4, the magic constant MC = 34.

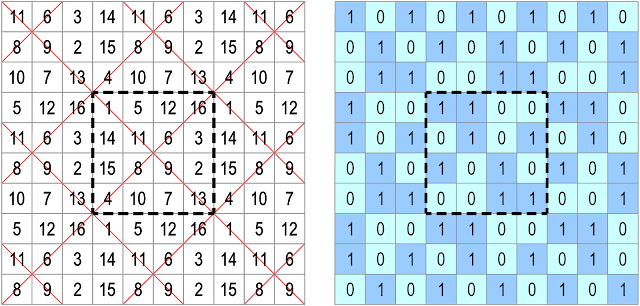
Extra-Magic Pandiagonal Torus T4.198 (type n° T4.01.2) of Order-4
with 16 Extra-Magic Intersections

Extra-Magic Pandiagonal Torus T4.198 of Order-4

Please note that here the torus viewpoint is deliberately centred on the number node 6. This is not a standard magic square presentation, but it means to show that on the limitless surface of the magic torus there is no fixed centre. The maximum number of magic lines at intersections (at each number node) is 4. The total number of magic lines on the order-4 pandiagonal torus index n° T4.198 is 8 orthogonals (in red) + 8 classic diagonals (in red) = 16 magic lines.

There are a total of 3 Pandiagonal Tori type T4.01 that each display 16 pandiagonal squares. The corresponding 48 pandiagonal squares are Dudeney type I.

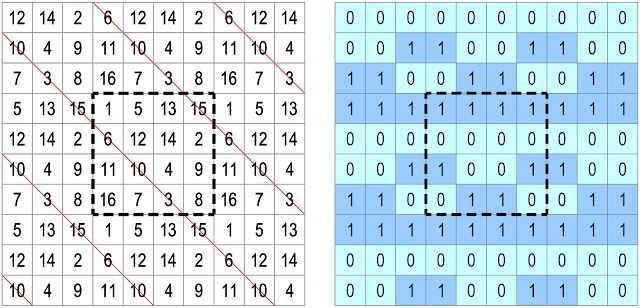
Extra-Magic Semi-Pandiagonal Torus T4.080 (type n° T4.02.3.02) of Order-4
with 8 Knight Move Magic Diagonals

Extra-Magic Semi-Pandiagonal Torus T4.080 of Order-4

The magic line graph of the semi-pandiagonal torus index n° T4.080 (type n° T4.02.3.02) is here presented as seen from the magic square viewpoint Frénicle n° 33. After the addition of knight move magic diagonals (1, 10, 16, 7) + (1, 7, 16, 10) + (11, 4, 6, 13) + (13, 11, 4, 6) + (8, 15, 9, 2) + (8, 2, 9, 15) + (14, 5, 3, 12) + (14, 12, 3, 5) the maximum number of magic lines at a nodal intersection is 5 (at each number node). The total number of magic lines on the magic torus is 8 orthogonals (in red) + 4 classic diagonals (in red) + 8 knight move diagonals (in blue) = 20 magic lines.

All of the 12 Semi-Pandiagonal Tori Type T4.02.3 have 8 knight move magic diagonals, and each torus displays 8 semi-pandiagonal squares. The corresponding 96 semi-pandiagonal squares are Dudeney type V.

Extra-Magic Partially Pandiagonal Torus T4.186 (type n° T4.03.1.3) of Order-4
with 4 Extra-Magic Intersections and 4 Knight Move Magic Diagonals

Extra-Magic Partially Pandiagonal Torus T4.186 of Order-4

The magic line graph of the partially pandiagonal torus index n° T4.186 (type n° T4.03.1.3) is here presented as seen from the magic square viewpoint Frénicle n° 793. After the addition of the knight move magic diagonals (3, 12, 13, 6) + (3, 6, 13, 12) + (4, 5, 14, 11) + (4, 11, 14, 5), the maximum number of magic lines at a nodal intersection is 6 (at extra-magic number nodes 4, 5, 13, 12). The total number of magic lines on the magic torus is 8 orthogonals (in red) + 4 classic diagonals (in red) + 4 knight move diagonals (in blue) = 16 magic lines.

2 out of the 6 Partially Pandiagonal Tori Type T4.03.1 have similar knight move magic diagonals (index n° T4.186 and T4.246), and both tori display 4 partially pandiagonal squares. The corresponding 8 partially pandiagonal squares are Dudeney Type VI.

Extra-Magic Partially Pandiagonal Torus T4.060 (type n° T4.03.2.07) of Order-4
with 4 Extra-Magic Intersections and 4 Knight Move Magic Diagonals

Extra-Magic Partially Pandiagonal Torus T4.060 of Order-4

The magic line graph of the partially pandiagonal torus index n° T4.060 (type n° T4.03.2.07) is here presented as seen from the magic square viewpoint Frénicle n° 472. After the addition of the knight move magic diagonals (1, 8, 14, 11) + (1, 11, 14, 8) + (5, 4, 10, 15) + (5, 15, 10, 4), the maximum number of magic lines at a nodal intersection is 6 (at extra-magic number nodes 4, 5, 11, 14). The total number of magic lines on the magic torus is 8 orthogonals (in red) + 4 classic diagonals (in red) + 4 knight move diagonals (in blue) = 16 magic lines.

All of the 12 Partially Pandiagonal Tori Type T4.03.2 have similar knight move magic diagonals, and each torus displays 4 partially pandiagonal squares. The corresponding 48 partially pandiagonal squares, which are evenly mixed on each torus, are either Dudeney type VII (24 squares), or Dudeney type IX (24 squares).

Extra-Magic Partially Pandiagonal Torus T4.187 (type n° T4.03.3.2) of Order-4
with 4 Extra-Magic Intersections and 4 Knight Move Magic Diagonals

Extra-Magic Partially Pandiagonal Torus T4.187 of Order-4

The magic line graph of the partially pandiagonal torus index n° T4.187 (type n° T4.03.3.2) is here presented as seen from the magic square viewpoint Frénicle n° 202. After the addition of the knight move magic diagonals (3, 4, 13, 14) + (3, 14, 13, 4) + (5, 6, 11, 12) + (5, 12, 11, 6) the maximum number of magic lines at a nodal intersection is 6 (at extra-magic number nodes 4, 5, 12, 13). The total number of magic lines on the magic torus is 8 orthogonals (in red) + 4 classic diagonals (in red) + 4 knight move diagonals (in blue) = 16 magic lines.

Both of the Partially Pandiagonal Tori Type T4.03.3 have similar knight move magic diagonals, and each torus displays 4 partially pandiagonal squares. The corresponding 8 partially pandiagonal squares are Dudeney type XI.

Extra-Magic Partially Pandiagonal Torus T4.096 (type n° T4.04.1) of Order-4
with 2 Extra-Magic Intersections

Extra-Magic Partially Pandiagonal Torus T4.096 of Order-4

The magic line graph of the partially pandiagonal torus index n° T4.096 (type n° T4.04.1) is here presented as seen from the magic square viewpoint Frénicle n° 40. The maximum number of lines at intersections (over the extra-magic number nodes 1 and 13) is 4. The total number of magic lines on the magic torus is 8 orthogonals (in red) + 3 classic diagonals (in red) = 11 magic lines.

The 4 Partially Pandiagonal Tori Type T4.04 have 2 extra-magic intersections, and each of these tori displays 2 partially pandiagonal squares. The corresponding 8 partially pandiagonal squares, which are evenly mixed on each torus, are either Dudeney type VIII (4 squares) or Dudeney type X (4 squares). The tori type T4.04 were initially found thanks to Walter Trump's computing skills.

Extra-Magic Basic Magic Torus T4.028 (type n° T4.05.1.78) of Order-4
with 4 Knight Move Magic Diagonals

Extra-Magic Basic Magic Torus T4.028 of Order-4

The magic line graph of the magic torus index n° T4.028 (type N° T4.05.1.78) is here presented as seen from the magic square viewpoint Frénicle n° 502. After the addition of knight move magic diagonals (1, 5, 13, 15) + (1, 15, 13, 5) + (2, 4, 12, 16) + (2, 16, 12, 4) the maximum number of magic lines at a nodal intersection is 5 (at number nodes 4, 5, 12, 13). The total number of magic lines on the magic torus is 8 orthogonals (in red) + 2 classic diagonals (in red) + 4 knight move diagonals (in blue) = 14 magic lines.

4 out of the 92 Basic Magic Tori Type T4.05.1 have 4 knight move magic diagonals (index n° T4.028, T4.102, T4.153 and T4.203), and each of these tori displays 2 basic magic squares. The corresponding 8 basic magic squares are Dudeney type VI.

Extra-Magic Basic Magic Torus T4.071 (type n° T4.05.1.35) of Order-4
with 8 Knight Move Magic Diagonals

Extra-Magic Basic Magic Torus T4.071 of Order-4

The magic line graph of the magic torus index n° T4.071 (type n° T4.05.1.35) is here presented as seen from the magic square viewpoint Frénicle n° 134. After the addition of knight move magic diagonals (1, 6, 15, 12) + (1, 12, 15, 6) + (2, 5, 16, 11) + (2, 11, 16, 5)+ (3, 8, 13, 10) + (3, 10, 13, 8) + (4, 7,14, 9) + (4, 9, 14, 7) the maximum number of magic lines at a nodal intersection is 5 (at number nodes 1, 4, 6, 8, 9, 11, 13, 16). The total number of magic lines on the magic torus is 8 orthogonals (in red) + 2 classic diagonals (in red) + 8 knight move diagonals (in blue) = 18 magic lines.

6 out of the 92 Basic Magic Tori Type T4.05.1 have 8 knight move magic diagonals (index n° T4.071, T4.076, T4.134, T4.140, T4.227 and T4.232), and each of these tori displays 2 basic magic squares. The corresponding 12 basic magic squares are Dudeney type VI.

Extra-Magic Basic Magic Torus T4.110 (type n° T4.05.2.29) of Order-4
with 4 Knight Move Magic Diagonals

Extra-Magic Basic Magic Torus T4.110 of Order-4

The magic line graph of the magic torus index n° T4.110 (type n° T5.05.2.29) is here presented as seen from the magic square viewpoint Frénicle n° 568. After the addition of knight move magic diagonals (1, 9, 11, 13) + (1, 13, 11, 9) + (4, 6, 8, 16) + (4, 16, 8, 6) the maximum number of magic lines at a nodal intersection is 5 (at number nodes 6, 8, 11, 13). The total number of magic lines on the magic torus is 8 orthogonals (in red) + 2 classic diagonals (in red) + 4 knight move diagonals (in blue) = 14 magic lines.

2 out of the 32 Basic Magic Tori Type T4.05.2 have 4 knight move magic diagonals (index n° T4.110 and T4.116), and both of these tori display 2 basic magic squares. The corresponding 4 basic magic squares, which are evenly mixed on each torus, are either Dudeney type VII (2 squares) or Dudeney type IX (2 squares).

Extra-Magic Semi-Magic Tori of Order-4

More details of the Semi-Magic Tori of Order-4 can be found in "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus".

Only consecutively numbered semi-magic tori (with numbers from 1 to n²) are studied here, and consequently, for the order-4, the magic constant MC = 34.

Extra-magic semi-magic tori of order-4 have neither been fully investigated nor precisely counted, and the examples shown below are a small selection of some of the different varieties.

Extra-Magic Semi-Magic Torus Type n° T4.06.0A of Order-4
with 8 Knight Move Magic Diagonals

Extra-Magic Semi-Magic Torus Type n° T4.06.0A of Order-4

The magic line graph of the semi-magic torus type n° T4.06.0A is based on a semi-magic torus that was first identified by Walter Trump. After the addition of knight move magic diagonals (1, 6, 16, 11) + (1, 11, 16, 6) + (2, 3, 15, 14) + (2, 14, 15, 3) + (4, 7, 13, 10) + (4, 10, 13, 7) + (5, 8, 12, 9) + (5, 9, 12, 8) the maximum number of magic lines at a nodal intersection is 5 (at all number nodes). The total number of magic lines on the semi-magic torus is 8 orthogonals (in red) + 4 classic diagonals (in red) + 8 knight move diagonals (in blue) = 20 magic lines.

Extra-Magic Semi-Magic Torus Type n° T4.07.0A of Order-4
with 4 Knight Move Magic Diagonals

Extra-Magic Semi-Magic Torus Type n° T4.07.0A of Order-4

The magic line graph of the semi-magic torus type n° T4.07.0A is based on a semi-magic torus that was first identified by Walter Trump. After the addition of knight move magic diagonals (1, 4, 13, 16) + (1, 16, 13, 4) + (2, 5, 12, 15) + (2, 15, 12, 5) the maximum number of magic lines at a nodal intersection is 5 (at number nodes 4, 5, 12, 13). The total number of magic lines on the semi-magic torus is 8 orthogonals (in red) + 2 classic diagonals (in red) + 4 knight move diagonals (in blue) = 14 magic lines.

Extra-Magic Tori of Order-5

In the Order-5, studies of knight move magic diagonals have previously been made by Miguel Angel Amela in his paper "Magic and Semi-Magic Squares of Order 5 - Rectangular Pandiagonality" dated Spring 2011: Here he has identified 144 magic squares and 3456 semi-magic squares with "rectangular pandiagonality", and he has kindly authorised me to use one of these for an illustration of this extra-magic in a basic magic torus of the order-5.

Only consecutively numbered magic tori (with numbers from 1 to n²) are studied here, and consequently for the order-5, the magic constant MC = 65.

Extra-magic tori of order-5 have neither been fully investigated nor precisely counted, and the examples shown below are a small selection of some of the different varieties.

Extra-Magic Pandiagonal Torus Type T5.01
with 6 Knight Move Magic Diagonals

Extra-Magic Pandiagonal Torus Type T5.01 of Order-5

This magic line graph, based on a pandiagonal torus type T5.01 of order-5, attributed to Philippe de la Hire (c. 1705) by Percy Alexander MacMahon in his 1902 paper "Magic Squares and Other Problems upon a Chess Board", shows the presence of extra-magic with 6 knight move magic diagonals. After taking these into account, the maximum number of magic lines at a nodal intersection is 8 (at number nodes 12 and 13). The total number of magic lines on the pandiagonal torus is 10 orthogonals (in red) + 10 classic diagonals (in red) + 6 knight move diagonals (in blue) = 26 magic lines.

Extra-Magic Partially Pandiagonal Torus Type n° T5.03.00A of Order-5
with 2 Knight Move Magic Diagonals

Extra-Magic Partially Pandiagonal Torus Type T5.03 of Order-5

This magic line graph, based on a partially pandiagonal torus type n° T5.03.00A of order-5 found by Walter Trump in 2012, shows the presence of extra-magic with 2 knight move magic diagonals. After the addition of the knight move diagonals (5, 9, 17, 21, 13) and (5, 17, 13, 9, 21), the maximum number of magic lines at a nodal intersection is 6 (at number nodes 5 and 21). The total number of magic lines on the partially pandiagonal torus is 10 orthogonals (in red) + 7 classic diagonals (in red) + 2 knight move diagonals (in blue) = 19 magic lines.

Extra-Magic Partially Pandiagonal Torus Type n° T5.04.000A of Order-5
with 2 Knight Move Magic Diagonals

Extra-Magic Partially Pandiagonal Torus Type T5.04 of Order-5

This magic line graph, based on a partially pandiagonal torus type n° T5.04.000A of order-5 found by Walter Trump in 2012, shows the presence of extra-magic with 2 knight move magic diagonals. After the addition of the knight move diagonals (6, 9, 15, 11, 24) and (6, 11, 9, 24, 15), the maximum number of magic lines at a nodal intersection is 6 (at number nodes 11 and 15). The total number of magic lines on the partially pandiagonal torus is 10 orthogonals (in red) + 6 classic diagonals (in red) + 2 knight move diagonals (in blue) = 18 magic lines.

Extra-Magic "Knight's Tour" Partially Pandiagonal Torus Type T5.06 of Order-5
with 12 Knight Move Magic Diagonals

Extra-Magic "Knight's Tour" Partially Pandiagonal Torus Type T5.06 of Order-5

This magic line graph, based on a "knight's tour" partially pandiagonal torus type T5.06 of order-5, published by William Symes Andrews in his book "Magic Squares and Cubes" in 1908 (figure 20), shows the presence of extra-magic with 12 knight move magic diagonals. After the addition of the knight move magic diagonals, the maximum number of magic lines at a nodal intersection is 8 (at number node 13). The total number of magic lines on the partially pandiagonal torus is 10 orthogonals (in red) + 6 classic diagonals (in red) + 12 knight move diagonals (in blue) = 28 magic lines.

Extra-Magic Basic Magic Torus Type T5.10 of Order-5
with 20 Knight Move Magic Diagonals

Extra-Magic Basic Magic Torus Type T5.10 of Order-5

This magic line graph, based on a basic magic torus type T5.10 of order-5 published by Miguel Angel Amela in his paper "Magic and Semi-Magic Squares of Order 5 - Rectangular Pandiagonality" in spring 2011, shows the presence of extra-magic with knight move pandiagonality. After the addition of the knight move magic diagonals, the maximum number of magic lines at a nodal intersection is 8 (at number node 13). The total number of magic lines on the magic torus is 10 orthogonals (in red) + 2 classic diagonals (in red) + 20 knight move diagonals (in blue) = 32 magic lines.

In order-5, Miguel Angel Amela has found a total of 144 Magic Tori with "Rectangular Pandiagonality". Each of these displays 1 magic square and 24 semi-magic squares, and the corresponding grand totals are therefore 144 magic squares and 3456 semi-magic squares with knight move pandiagonality!

Extra-Magic Semi-Magic Torus of Order-5

Extra-magic semi-magic tori of order-5 have neither been fully investigated nor precisely counted, and the example shown below is randomly chosen.

Extra-Magic Semi-Magic Torus Type n° T5.14000000000X of Order-5
with 4 Knight Move Magic Diagonals

Extra-Magic Semi-Magic Torus Type T5.14 of Order-5

This magic line graph of a semi-magic torus type n° T5.14.000000000X of order-5, shows the presence of extra-magic with 4 knight move magic diagonals. After the addition of the knight move magic diagonals (2, 12, 19, 22, 10), (2, 22, 12, 10, 19), (5, 8, 12, 24, 16) and (5, 24, 8, 16, 12), the maximum number of magic lines at a nodal intersection is 7 (at number node 12). The total number of magic lines on the semi-magic torus is 10 orthogonals (in red) + 1 classic diagonal (in red) + 4 knight move diagonals (in blue) = 15 magic lines.

Extra-Magic Tori of Order-6

In the Order-6, studies of knight move magic diagonals have previously been made by Miguel Angel Amela in his paper "Compact Magic and Semi-Magic Squares of Order n = 4k+2 - Rectangular Pandiagonality" dated Spring 2011, and Miguel has kindly authorised me to use one of his squares for an illustration of this extra-magic in a compact semi-magic torus of order-6.

Only consecutively numbered magic tori (with numbers from 1 to n²) are studied here, and consequently, for the order-6, the magic constant MC = 111.

Extra-magic tori of order-6 have neither been fully investigated nor precisely counted, and the examples shown below are selected samples of some of the different varieties.

Extra-Magic Partially Pandiagonal Torus of Order-6
with 6 Knight Move Magic Diagonals

Extra-Magic Partially Pandiagonal Torus of Order 6 with 6 KM Magic Diagonals

This magic line graph, based on a partially pandiagonal torus of order-6 which Harry White has kindly authorised me to use, shows the presence of extra-magic with 6 knight move magic diagonals. After the addition of the knight move magic diagonals, the maximum number of magic lines at a nodal intersection is 5 (at number nodes 19, 20, 22). The total number of magic lines on the partially pandiagonal torus is 12 orthogonals (in red) + 3 classic diagonals (in red) + 6 knight move diagonals (in blue) = 21 magic lines.

Extra-Magic Partially Pandiagonal torus of Order-6
with 16 Extra-Magic Intersections and 4 Knight Move Magic Diagonals

Extra-Magic Partially Pandiagonal Torus of Order-6 with 4 KM Magic Diagonals

This magic line graph, based on a partially pandiagonal torus of order-6 which Francis Gaspalou has kindly authorised me to use, shows the presence of both extra-magic intersections and knight move magic diagonals. After the addition of the knight move magic diagonals, the maximum number of magic lines at a nodal intersection is 6 (at number nodes 7, 11, 26, 30). The total number of magic lines on the partially pandiagonal torus is 12 orthogonals (in red) + 8 classic diagonals (in red) + 4 knight move diagonals (in blue) = 24 magic lines.

Extra-Magic Basic Magic Torus of Order-6
with 2 Knight Move Magic Diagonals

Extra-Magic Basic Magic Torus of Order-6 with 2 KM Magic Diagonals

This magic line graph, based on a basic magic torus of order-6 by William Symes Andrews in figure 311 of the 1917 re-edition of his book "Magic Squares and Cubes", shows the presence of extra-magic with 2 knight move magic diagonals. After the addition of the knight move magic diagonals, the maximum number of magic lines at a nodal intersection is 4 (at number nodes 5, 14, 23, 32). The total number of magic lines on the basic magic torus is 12 orthogonals (in red) + 2 classic diagonals (in red) + 2 knight move diagonals (in blue) = 16 magic lines.

Extra-Magic Semi-Magic Tori of Order-6

Extra-magic semi-magic tori of order-6 have neither been fully investigated nor precisely counted, and the examples shown below are selected samples of some of the different varieties.

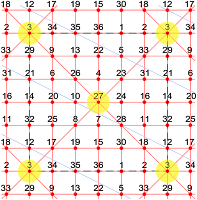
Extra-Magic Semi-Magic Torus of Order 6
with 2 Extra-Magic Intersections and 1 Knight Move Magic Diagonal

Extra-Magic Semi-Magic Torus of Order-6 with 1 KM Magic Diagonal

This magic line graph, based on a semi-magic torus of order-6 previously found by Walter Trump and already illustrated in "Sixth and Higher-Order Magic Tori", shows not only the presence of 2 extra-magic intersections, but also a single knight move magic diagonal. (The latter was not noticed at the time of the first illustration). Please note that here the torus viewpoint is deliberately centred on the number node 27. This is not a standard magic square presentation, but it means to show that on the limitless surface of the magic torus there is no fixed centre. After the addition of the knight move magic diagonal, the maximum number of magic lines at intersections (number nodes 3, 27, 28) is 4. The total number of magic lines on the semi-magic torus is 12 orthogonals (in red) + 2 classic diagonals (in red) + 1 knight move diagonal (in blue) = 15 magic lines.

Extra-Magic Compact Semi-Magic Torus of Order-6
with 24 Knight Move Magic Diagonals

Extra-Magic Compact Semi-Magic Torus of Order-6 with 24 KM Magic Diagonals

This magic line graph is based on a compact semi-magic torus of order-6 with knight move pandiagonality, found by Miguel Angel Amela and published in his 2011 paper "Compact Magic and Semi-Magic Squares of Order n = 4k+2 - Rectangular Pandiagonality". After the addition of the knight move magic diagonals, the maximum number of magic lines at a nodal intersection is 6 (at all number nodes). The total number of magic lines on the semi-magic magic torus is 12 orthogonals (in red) + 0 classic diagonals (in red) + 24 knight move diagonals (in blue) = 36 magic lines.

In a compact magic square, the sum of each 2 x 2 subsquare is equal to 4/n of the magic constant (MC), and for the order-6 the sum of each of the 2 x 2 subsquares is therefore equal to 4/6 x 111 = 74. Miguel Amela proves that, regardless of whether they are magic or semi-magic, all compact squares of orders n = 4k+2 are also knight move pandiagonal. Taking into account squares with consecutive numbers from 1 to n², he has calculated that there are 53136 compact (and therefore knight move pandiagonal) semi-magic squares of order-6. This implies that there are 1476 compact semi-magic tori with these characteristics in order-6.

Extra-Magic Tori of Order-7

In the Order-7, studies of knight move magic diagonals have previously been made by Miguel Angel Amela and he has kindly authorised me to use one of his basic magic squares for an illustration of knight move pandiagonality.

Only consecutively numbered magic tori (with numbers from 1 to n²) are studied here, and consequently, for the order-7, the magic constant MC = 175.

Extra-magic tori of order-7 have neither been fully investigated nor precisely counted, and the examples shown below are selected samples of some of the different varieties.

Extra-Magic "Knight's Tour" Pandiagonal Torus of Order-7
with 16 Knight Move Magic Diagonals

Extra-Magic "Knight Tour" Pandiagonal Torus of Order-7 with 16 KM Magic Diagonals

This magic line graph is based on a "knight's tour" pandiagonal Torus of Order-7 published by Emory McClintock in his 1896 paper "On the Most Perfect Forms of Magic Squares, with Methods for their Production" (figure A): Although McClintock mentions "leaper" moves such as the Zebra (3, -2) in the description of his construction method by "step summation", he does not point out the traditional knight move magic diagonal characteristics of his pandiagonal square. After the addition of the 16 knight move magic diagonals that we find on this torus, the maximum number of magic lines at a nodal intersection is 8 (at number node 25). The total number of magic lines on the pandiagonal torus is 14 orthogonals (in red) + 14 classic diagonals (in red) + 16 knight move diagonals (in blue) = 44 magic lines.

Extra-Magic "Knight's Tour" Partially Pandiagonal Torus of Order-7
with 22 Knight Move Magic Diagonals

Extra-Magic "Knight Tour" Partially Pandiagonal Torus of Order-7 with 22 KM Magic Diagonals

This magic line graph is based on a "knight's tour" partially pandiagonal torus of order-7 that George Jelliss has kindly authorised me to use. After the addition of the 22 knight move magic diagonals, the maximum number of magic lines at a nodal intersection is 8 (at number node 25). George Jelliss points out that the "geometry of 'straight lines' is distinctly non-euclidean." For example, numbers such as (22, 23, 24, 25, 26, 27, 28) are connected in at least 3 different ways along knight (1, 2), camel (3, -1), and zebra (2, -3) move magic diagonals, and many more possibilities exist if we stretch out the knight move steps even further... But here we only take into account the traditional knight move magic diagonals, and the total number of magic lines on the partially pandiagonal torus is therefore 14 orthogonals (in red) + 8 classic diagonals (in red) + 22 knight move diagonals (in blue) = 44 magic lines.

Extra-Magic Basic Magic Torus of Order-7
with 28 Knight Move Magic Diagonals

Extra-Magic Basic Magic Torus of Order-7 with 28 KM Magic Diagonals

This magic line graph is based on a knight move pandiagonal basic magic torus of order-7 that Miguel Angel Amela has kindly authorised me to use. This torus was probably created when he wrote his paper "Magic and Semi-Magic Squares of Order 5 - Rectangular Pandiagonality" in spring 2011. After the addition of the knight move magic diagonals, the maximum number of magic lines at a nodal intersection is 8 (at number node 25). The total number of magic lines on the basic magic torus is 14 orthogonals (in red) + 2 classic diagonals (in red) + 28 knight move diagonals (in blue) = 44 magic lines.

An Extra-Magic Semi-Magic Torus of Order-7

Extra-magic semi-magic tori of order-7 have neither been fully investigated nor precisely counted, and the example shown below is randomly chosen.

Extra-Magic Semi-Magic Torus of Order-7
with 6 Knight Move Magic Diagonals

Extra-Magic Semi-Magic Torus of Order-7 with 6 KM Magic Diagonals

This magic line graph of a semi-magic torus of order-7 shows the presence of 6 knight move magic diagonals. The maximum number of magic lines at a nodal intersection is 5 (at number nodes 12, 28, 35 and 39). The total number of magic lines on the semi-magic torus is 14 orthogonals (in red) + 3 classic diagonals (in red) + 6 knight move diagonals (in blue) = 23 magic lines.

Extra-Magic Tori of Order-8

Of the same format as traditional chessboards, magic squares of order-8 have not only been the focus of much previous research into "knights' tours", but have also been (since 1877, if not earlier) the subject of studies of knight move magic diagonals. Further historical details are given in the observations made after the analysis of a "Caïssan Beauty", studied below.

Only consecutively numbered magic tori (with numbers from 1 to n²) are studied here, and consequently, for the order-8, the magic constant MC = 260.

Extra-magic tori of order-8 have neither been fully investigated nor precisely counted, and the examples shown below are selected samples of some of the different varieties.

Extra-Magic "Caïssan Beauty" Pandiagonal Torus of Order-8
with 64 Extra-Magic Intersections and 32 Knight Move Magic Diagonals

Extra-Magic "Caïssan Beauty" Pandiagonal Torus of Order-8 with 32 KM Magic Diagonals

This magic line graph, based on a "Caïssan Beauty" pandiagonal torus of order-8 created by Nārāyana Pandita (Sanskrit: नारायण पण्डित) in 1356, shows the presence of 64 extra-magic intersections as well as knight move pandiagonality. The maximum number of magic lines at nodal intersections is 8 (at all number nodes). The total number of magic lines on the "Caïssan Beauty" pandiagonal torus is 16 orthogonals (in red) + 16 classic diagonals (in red) + 32 knight move diagonals (in blue) = 64 magic lines.

First published by Nārāyana Pandita in his 1356 "Gaṇita Kaumudī" (Part II), an original version of the torus can be seen online, on page 396 of a 1942 reprint. Only those versed in Sanskrit will be able to read whether Nārāyana Pandita mentioned the knight move pandiagonal characteristics.

What we know for sure is that in 1877, Andrew Hollingworth Frost wrote an article "On the General Properties of Nasik Squares" in "The Quarterly Journal of Pure and Applied Mathematics", Volume 15, in which he presented the same Nārāyana Pandita torus seen from a different magic square viewpoint, referring to a diagram S in his description: "By the method adopted in No. XXV. 1865, of this Journal, squares of the form 4n had four summations only, in the lines of the row [sic], columns, and diagonals. This square has ten summations through each number, as shewn in the diagram S, the hollow dots giving the pathlets of contsruction [sic]." After verification of the diagram S, we see that it shows 2 orthogonal pathlets, 2 diagonal (1, 1) pathlets, 2 diagonal (1, 2) pathlets, 2 diagonal (2, 1) pathlets, 2 diagonal (1, 3) pathlets = 10 pathlets! Although this is a clearly documented example of the early awareness of knight move magic diagonals, Frost may have been preceded by others... 

Please note that the initial intention of the present article "Extra-Magic Tori and Knight Move Magic Diagonals" was to limit the study to classic knight moves, and it was only because Frost had integrated (1, 3) leaper pathlets in his Diagram S, that it was decided to make an exception for the analysis of the Caïssan Beauty, and additionally count camel moves for this particular case. However, Frost only takes into account 2 out of the 4 camel move diagonal (1, 3) pathlets, ignoring the dissimilar paths that use a same magic series... And in the present article we count separately the same-series pathlets having different magic sequences and dissimilar paths, so our count gives a total of 12 pathlets. Please refer to "Knight Move Magic Diagonals", at the beginning of the blog article, where this phenomena is already pointed out and a link is provided towards a file dated 7th August 2019, entitled "Knight Move Magic Diagonals on Magic Tori". The file explains why knight move (and by extrapolation, other leaper move magic diagonals) can have 2 different paths for a same series of numbers.

In 1881, "Ursus" (Henry James Kesson?) wrote an article entitled "Caïssan Magic Squares" in "The Queen, The Lady's Newspaper & Court Chronicle", presenting the same Nārāyana Pandita torus,seen from yet another magic square viewpoint, in his Figure D. "Ursus" was clearly aware of all the chess move magic diagonals, and he defined a magic square to be Caïssan whenever it was pandiagonal and knight-Nasik. "Ursus" seems to have been the first person to explicitly connect "Caïssa" (named as the patron goddess of chess players by Sir William Jones in his 1763 "Caïssa, or The Game at chess, a poem") with magic squares.

In 1900, Charles Planck wrote an article entitled "The n queens problem" in "The British Chess Magazine", and presented the same Nārāyana Pandita torus, seen from a once again different magic square viewpoint in his Figure II, stating that he believed it to be the "first complete Caïssan square of 64 cells which has been constructed"!

Although the different magic square viewpoints of Nārāyana Pandita's original that were presented by these distinguished authors were certainly coincidental, it is a relief to find at least one writer of the same period who produced two totally original "Caissan Beauties": In 1896, Emory McClintock presented a paper to the American Mathematical Society entitled "On the Most Perfect Forms of Magic Squares, with Methods for their Production" in which his squares D and E were refreshingly new examples, both coming from completely different "Caïssan Beauty" pandiagonal tori. 

George P. H. Styan has written an excellent paper entitled "An illustrated introduction to Caïssan squares: the magic of chess". Published in 2012, in Volume 16, Number 1, of "Acta et Commentationes Universitatis Tartuensis de Mathematica" it retraces the history of Caïssan squares in great detail with numerous references, and I fully recommend it to readers who wish to learn more.

Extra-Magic Partially Pandiagonal Torus of Order-8
with 32 Extra-Magic Intersections and 4 Knight Move Magic Diagonals

Extra-Magic Partially Pandiagonal Torus of Order-8 with 4 KM Magic Diagonals

This magic line graph, based on a partially pandiagonal torus of order-8 which Walter Trump has kindly authorised me to use, shows not only the presence of 32 extra-magic intersections but also 4 knight move magic diagonals. (The torus is also bimagic, but the squared version has no such diagonals). After the addition of the knight move magic diagonals, the maximum number of magic lines at a nodal intersection is 5 (at 16 number nodes 6, 7, 14, 15, 22, 23, 30, 31, 34, 35, 42, 43, 50, 51, 58, 59). The total number of magic lines on the partially pandiagonal torus is 16 orthogonals (in red) + 12 classic diagonals (in red) + 4 knight move diagonals (in blue) = 32 magic lines.

Extra-Magic Semi-Magic Torus of Order-8

Extra-magic semi-magic tori of order-8 have neither been fully investigated nor precisely counted, and although only one of many, the example below is specifically chosen for its historical importance.

Extra-Magic Semi-Magic "Knight's Tour" Torus of Order-8
with 2 Knight Move Magic Diagonals

Extra-Magic Semi-Magic "Knight Tour" Torus of Order-8 with 2 KM Magic Diagonals

This magic line graph is based on the first semi-magic knight's tour torus that was created by William Roxby Beverley and published as a letter dated 5th June 1847 "On the Magic Square of the Knight's March" in the August 1848 edition of "The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science". After the addition of the knight move magic diagonals, the maximum number of magic lines at a nodal intersection is 3 (at 16 number nodes 7, 8, 9, 10, 33, 34, 35, 36, 37, 38, 43, 44, 45, 46, 46, and 48). The total number of magic lines on the semi-magic torus is 16 orthogonals (in red) + 0 classic diagonals (in red) + 2 knight move diagonals (in blue) = 18 magic lines. 

More information about William Beverley is given in the "History of Knight Tours" and "Magic Knight Tours" by George Jelliss. At this stage it is useful to point out that Beverley's first semi-magic knight's tour square of order-8 has sometimes been mistakenly attributed to Leonhard Euler by otherwise reputable sources, and although Euler did indeed present knights' tours in his "Solution d'une question curieuse qui ne paroit soumise a aucune analyse" which was published in 1759, none of his solutions were either semi-magic or magic!

Observations

The Impact of Knight Move Magic Diagonals

Once we take knight move magic diagonals into account, this can modify our perception of the "most magic" solutions. In this study we have only used traditional knight move steps and there are already many examples with a dense weave of magic lines. What a magic line graph looks like after the addition of non-traditional knight move lines is difficult to say, but we can anticipate that in several cases there will be very little blank space, or even none whatsoever...

In order-4, we immediately notice that the total number of magic lines of a pandiagonal torus type T4.01 (which has 12 magic lines) is inferior to the total number of lines of the extra-magic semi-pandiagonal torus type n° T4.02.3 (which has 20 magic lines). Also, 2 out of 6 partially pandiagonal tori type T4.03.1, and each of the partially pandiagonal tori types T4.03.2 and T4.03.3 have 16 magic lines, which is more than the number of magic lines of a pandiagonal torus type T4.01. Even the basic magic tori with knight move magic diagonals have a greater number of magic lines than the pandiagonal torus: 4 of the basic magic tori type T4.05.1 have 14 magic lines and 6 have 18 magic lines, whist 2 of the basic magic tori type T4.05.2 again have 14 magic lines. What is perhaps more surprising is that semi-magic tori such as the torus types T4.06.0A and T4.07.0A have respectively 20 and 14 magic lines; both examples exceeding the pandiagonal torus T4.01 in their magic line totals. The semi-magic torus type T4.06.0A even equals the highest number of magic lines of the "most magic" semi-pandiagonal torus type T4.02.3! As the semi-magic tori of order-4 have not yet been explored in detail, there may be other "more magic" cases that remain to be discovered...

In order-5, there are also surprises, and without going into all the detail it can be seen that a basic magic torus type T5.10 with knight move pandiagonality has a total of 32 magic lines, which is many more than that of a pandiagonal torus type T5.01, which only has 6 knight move diagonals and a total of 26 magic lines. The order-5 has not been completely explored, so there may be other cases that will modify our appreciation of which tori are the "most magic".

In order-6, there are no pandiagonal tori when using consecutive numbers from 1 to n², as Charles Planck proved in his 1919 Monist article "Pandiagonal Magics of Orders 6 and 10 with Minimal Numbers". In the magic line graphs that are illustrated here, a partially pandiagonal example with 4 knight move magic diagonals has 24 magic lines; a basic magic example with 2 knight move magic diagonals has 16 magic lines; and a compact semi-magic example with knight move pandiagonality has 36 magic lines! Another semi-magic example worthy of interest is the torus with 1 knight move magic diagonal, and 2 extra-magic intersections of 6 magic lines, giving a total of 15 magic lines: This also exceeds the total number of magic lines of a "regular" basic magic torus of order-6, which, with 12 orthogonals + 2 diagonals, has only 14 magic lines.

In order-7, a "knight's tour" pandiagonal torus with 16 knight move magic diagonals, a "knight's tour" partially pandiagonal torus with 22 knight move magic diagonals, and a basic magic torus that is knight move pandiagonal, all have the same total of 44 magic lines.

In order-8, the "Caïssan Beauty" with 64 = n² magic lines is a pure marvel for both magic square and chess enthusiasts!

It can be seen that semi-magic tori (and the semi-magic squares that they display) often rival, and sometimes even better their magic tori cousins when we include the knight move magic diagonals in the counts of the magic lines. A reappraisal of the definitions seems to be called for. Both magic and semi-magic tori have almost similar magic weaves, so logically no hard distinction should be made between them.

Knight Move Bimagic Diagonals

In the squared version of the extra-magic partially pandiagonal torus of order-8 (with 32 extra-magic intersections and 4 knight move magic diagonals) tested above, it was disappointing to find no knight move bimagic diagonals. When testing another likely candidate , the order-32 square constructed by Su Maoting in February 2006 (which is the first known normal pandiagonal bimagic square using consecutive integers, and downloadable from Christian Boyer's Multimagic Squares site), it turns out to have 64 knight move magic diagonals, but once again, none of these are bimagic.

It is therefore still an open question as to whether knight move bimagic diagonals exist on bimagic tori, and if so, whether there are cases with knight move bimagic pandiagonality.

The Geometry of Knight Move Lines

It is interesting to note that when 3 traditional knight move magic lines form a triangle, then this triangle will always be Pythagorean, with a 3 : 4 : 5 proportion. This and other observations on knight move geometry are discussed further on the web page "Geometry of Knight's Moves" by George Jelliss. The geometry of other non-traditional "leapers" can be found on two more of his pages: "Theory of Moves" and "Theory of Journeys".

Acknowledgements

My special thanks go to Miguel Angel Amela, for his invaluable assistance in the search for previous documentation on knight move magic diagonals, and for taking the time to check and confirm my findings concerning the knight move magic diagonals of the magic tori of order-4. Miguel has also kindly authorised me to append his papers "Magic and Semi-Magic Squares of Order 5 - Rectangular Pandiagonality" and  "Compact Magic and Semi-Magic Squares of Order n = 4k+2 - Rectangular Pandiagonality" to this post, and has given me his permission to use his knight move pandiagonal squares of orders 5, 6 and 7 for magic line graphs.

Although, to the best of my knowledge, all of the magic line graphs illustrated here are original, many of them are based on magic squares or magic tori that have been constructed by others:

In the public domain we find the Lo Shu magic square of order-3 by Anonymus, and the magic squares of order-4, once again by Anonymus (but first listed by Bernard Frénicle de Bessy). Also coming from the public domain, because they were published before 1923, other magic squares used here include a pandiagonal square of order-5 attributed to Philippe de la Hire by Percy Alexander MacMahon; a "knight's tour" partially pandiagonal square of order-5 together with a basic magic square of order-6 by William Symes Andrews; a "knight's tour" pandiagonal square of order-7 by Emory McClintock; a "Caïssan Beauty" pandiagonal square of order-8 created by Nārāyana Pandita; and  a "knight's tour" semi-magic square by William Roxby Beverley. Each of these authors deserves to be remembered.

Contributions of other magic tori or magic squares, by the magic square specialists of today, include (in the order of the authors' appearance) the semi-magic tori T4.06.0A and T4.07.0A of order-4, the partially pandiagonal tori T5.03.00A T5.04.000A of order-5, a semi-magic torus of order-6, and a partially pandiagonal bimagic torus of order-8 by Walter Trump; a basic magic torus T5.10 of order-5, a compact semi-magic torus of order-6, and a basic magic torus of order-7 (all knight move pandiagonal) by Miguel Angel Amela; a partially pandiagonal torus of order-6 by Harry White; a partially pandiagonal torus of order-6 by Francis Gaspalou; and a "knight's tour" partially pandiagonal torus of order-7 by George Jelliss. My hearty thanks go to each of these authors for allowing me to use their work. Without their contributions, certain magic line graphs of this paper would not have been possible.

The sites that host the hyperlinked documentation include (in the order of their "appearance") Prime Puzzles, Wikipedia, Google Books, Nature, Internet Archive, JStor, Mayhematics, Wikisource, The University of Tartu, McGill University, Multimagic Squares, and Bibnum Education.

Latest Developments

On the 20th August 2019 Greg Ross published an article entitled "Magicker" on the subject of knight move magic diagonals in his Futility Closet - An Idler's Miscellany of Compendious Amusements.

Read more ...