Polyomino Area Magic Tori

A magic torus can be found with any magic square, as has already been demonstrated in the article "From the Magic Square to the Magic Torus". In fact, there are n² essentially different semi-magic or magic squares, displayed by every magic torus of order-n. Particularly interesting to observe with pandiagonal (or panmagic) examples, a magic torus can easily be represented by repeating the number cells of one of its magic square viewpoints outside its limits. However, once we begin to look at area magic squares, it becomes much less evident to visualise and construct the corresponding area magic tori using repeatable area cells, especially when the latter have to be irregular quadrilaterals... The following illustration shows a sketch of an area magic torus of order-3 that I created back in January 2017. I call it a sketch because it may be necessary to use consecutive areas starting from 2 or from 3, should the construction of an area magic torus of order-3, using consecutive areas from 1 to 9, prove to be impossible. And while it can be seen that such a torus is theoretically constructible, many calculations will be necessary to ensure that the areas are accurate, and that the irregular quadrilateral cells can be assembled with precision:

At the time discouraged by the complications of such geometries, I decided to suspend the research of area magic tori. But since the invention of area magic squares, other authors have introduced some very interesting polyomino versions that open new perspectives: 

On the 20th May 2021, Morita Mizusumashi (盛田みずすまし @nosiika) tweeted a nice polyomino area magic square of order-3 constructed with 9 assemblies of 5 to 13 monominoes. On the 21st May 2021, Yoshiaki Araki (面積魔方陣がテセレーションみたいな件 @alytile) tweeted several order-4 and order-3 solutions in a polyomino area magic square thread. These included (amongst others) an order-4 example constructed with 16 assemblies of 5 to 20 dominoes. On the 24th May 2021, Yoshiaki Araki then tweeted an order-3 polyomino area magic square constructed using 9 assemblies of 1 to 9 same-shaped pentominoes! Edo Timmermans, the author of this beautiful square, had apparently been inspired by Yoshiaki Araki's previous posts! Since the 22nd June 2021, Inder Taneja has also published a paper entitled "Creative Magic Squares: Area Representations" in which he studies polyomino area magic using perfect square magic sums.

Intention and Definition

The intention of the present article is to explore the use of polyominoes for area magic torus construction, with the objective of facilitating the calculation and verification of the cell areas, while avoiding the geometric constraints of irregular quadrilateral assemblies. Here, it is useful to give a definition of a polyomino area magic torus:

1/ In the diagram of the torus, the entries of the cells of each column, row, and of at least two intersecting diagonals, will add up to the same magic sum. The intersecting magic diagonals can be offset or broken, as the area magic torus has a limitless surface, and can therefore display semi-magic square viewpoints.

2/ Each cell will have an area in proportion to its number. The different areas will be represented by tiling with same-shaped holeless polyominoes.

3/ The cells can be of any regular or irregular rectangular shape that results from their holeless tiling. 

4/ Depending on the order-n of the area magic torus, each cell will have continuous edge connections with contiguous cells (and these connections can be wrap-around, because the torus diagram represents a limitless curved surface).

5/ The vertex meeting points of four cells can only take place at four convex (i.e. 270° exterior  angled) vertices of each of the cells.

Polyomino Area Magic Tori (PAMT) of Order-3

Magic Torus index n° T3, of order-3. Magic sums = 15.
Please note that this is not a Polyomino Area Magic Torus,
but it is the Agrippa "Saturn" magic square, after a rotation of +90°, in Frénicle standard form.

Polyomino Area Magic Torus (PAMT) of order-3. Magic sums = 15. Tetrominoes.
Consecutively numbered areas 1 to 9, in an irregular rectangular shape of 180 units.

Polyomino Area Magic Torus (PAMT) of Order-3. Magic sums = 18. Trominoes.
Consecutively numbered areas 2 to 10, in an irregular rectangular shape of 162 units.

Polyomino Area Magic Torus (PAMT) of order-3. Magic sums = 24. Trominoes.
Consecutively numbered areas 4 to 12, in an oblong 12 ⋅ 18 = 216 units.

Polyomino Area Magic Torus (PAMT) of Order-3. Magic sums = 36. Trominoes Version 1.
Square 18 ⋅ 18 = 324 units.

Polyomino Area Magic Torus (PAMT) of Order-3. Magic sums = 36. Trominoes Version 2.
Square 18 ⋅ 18 = 324 units.

Polyomino Area Magic Torus (PAMT) of Order-3. Magic sums = 60. Pentominoes Version 1.
Square 30 ⋅ 30 = 900 units.

Polyomino Area Magic Torus (PAMT) of order-3. Magic sums = 24. Monominoes.
Consecutively numbered areas 4 to 12, in an irregular rectangular shape of 72 units.

Polyomino Area Magic Torus (PAMT) of order-3. Magic sums = 27. Monominoes Version 1.
Consecutively numbered areas 5 to 13, in a square 9 ⋅ 9 = 81 units.

Polyomino Area Magic Torus (PAMT) of order-3. Magic sums = 27. Monominoes Version 2.
Consecutively numbered areas 5 to 13, in a square 9 ⋅ 9 = 81 units.

Polyomino Area Magic Tori (PAMT) of Order-4

Magic Torus index n° T4.198, of order-4. Magic sums = 34.
Please note that this is not a Polyomino Area Magic Torus,
but it is a pandiagonal torus represented by a pandiagonal square that has Frénicle index n° 107.

The pandiagonal torus above displays 16 Frénicle indexed magic squares n° 107, 109, 171, 204, 292, 294, 355, 396, 469, 532, 560, 621, 691, 744, 788, and 839. It is entirely covered by 16 sub-magic 2x2 squares. The torus is self-complementary and has the magic torus complementary number pattern I. The even-odd number pattern is P4.1. This torus is extra-magic with 16 extra-magic nodal intersections of 4 magic lines. It displays pandiagonal Dudeney I Nasik magic squares. It is classified with a Magic Torus index n° T4.198, and is of Magic Torus type n° T4.01.2. Also, when compared with its two pandiagonal torus cousins of order-4, the unique Magic Torus T4.198 of the Multiplicative Magic Torus MMT4.01.1 is distinguished by its total self-complementarity.

Pandiagonal Polyomino Area Magic Torus (PAMT) of order-4. Magic sums = 34. Pentominoes.
Index PAMT4.198, Version 1, Viewpoint 1/16, displaying Frénicle magic square index n° 107.
Consecutively numbered areas 1 to 16, in an oblong 34 ⋅ 20 = 680 units.

Pandiagonal Polyomino Area Magic Torus (PAMT) of order-4. Magic sums = 50. Dominoes.
Version 1, Viewpoint 1/16.
Consecutively numbered areas 5 to 20, in a square 20 ⋅ 20 = 400 units.

Pandiagonal Polyomino Area Magic Torus (PAMT) of Order-4. Sums = 50. Dominoes.
Version 1, Viewpoint 16/16.
Consecutively numbered areas 5 to 20, in an irregular rectangular shape of 400 units.

Polyomino Area Magic Tori (PAMT) of Order-5

Pandiagonal Torus type n° T5.01.00X of order-5. Magic sums = 65.
Please note that this is not a Polyomino Area Magic Torus.

This pandiagonal torus of order-5 displays 25 pandiagonal magic squares. It is a direct descendant of the T3 magic torus of order-3, as demonstrated in page 49 of "Magic Torus Coordinate and Vector Symmetries" (MTCVS). In "Extra-Magic Tori and Knight Move Magic Diagonals" it is shown to be an Extra-Magic Pandiagonal Torus Type T5.01 with 6 Knight Move Magic Diagonals. Note that when centred on the number 13, the magic square viewpoint becomes associative. The torus is classed under type n° T5.01.00X (provisional number), and is one of 144 pandiagonal or panmagic tori type 1 of order-5 that display 3,600 pandiagonal or panmagic squares. On page 72 of "Multiplicative Magic Tori" it is present within the type MMT5.01.00x.

Pandiagonal Polyomino Area Magic Torus (PAMT) of order-5. Magic sums = 65. Hexominoes.
Index PAMT5.01.00X, Version 1, Viewpoint 1/25.
Consecutively numbered areas 1 to 25, in an oblong 65 ⋅ 30 = 1950 units.

Pandiagonal Polyomino Area Magic Torus (PAMT) of Order-5. Magic sums = 125. Monominoes.
Version 1, Viewpoint 1/25.
Consecutively numbered areas 13 to 37, in a square 25 ⋅ 25 = 625 units.

Pandiagonal Polyomino Area Magic Torus (PAMT) of Order-5. Magic sums = 125. Monominoes.
Version 2, Viewpoint 1/25.
Consecutively numbered areas 13 to 37, in a square 25 ⋅ 25 = 625 units.

Polyomino Area Magic Tori (PAMT) of Order-6

Partially Pandiagonal Torus type n° T6 of order-6. Magic sums = 111.
Please note that this is not a Polyomino Area Magic Torus.

Harry White has kindly authorised me to use this order-6 magic square viewpoint. With a supplementary broken magic diagonal (24, 19, 31, 3, 5, 29), this partially pandiagonal torus displays 4 partially pandiagonal squares and 32 semi-magic squares. In "Extra-Magic Tori and Knight Move Magic Diagonals" it is shown to be an Extra-Magic Partially Pandiagonal Torus of Order-6 with 6 Knight Move Magic Diagonals. This is one of 2627518340149999905600 magic and semi-magic tori of order-6 (total deduced from findings by Artem Ripatti - see OEIS A271104 "Number of magic and semi-magic tori of order n composed of the numbers from 1 to n^2").

Partially Pandiagonal Polyomino Area Magic Torus (PAMT) of order-6. Magic sums = 111.
Heptominoes, Version 1, Viewpoint 1/36.
Consecutively numbered areas 1 to 36, in an oblong 111 ⋅ 42 = 4662 units.

Partially Pandiagonal Polyomino Area Magic Torus (PAMT) of order-6. Sums = 147.
Dominoes, Version 1, Viewpoint 1/36.
Consecutively numbered areas 7 to 42, in a square 42 ⋅ 42 = 1764 units.

Observations

As they are the first of their kind, these Polyomino Area Magic Tori (PAMT) can most likely be improved: The examples illustrated above are all constructed with their cells aligned horizontally or vertically; and though it is convenient to do so, because it allows their representation as oblongs or squares, this method of constructing PAMT is not obligatory. Representations of PAMT that have irregular rectangular contours may well give better results, with less-elongated cells and simpler cell connections. 

While the use of polyominoes has the immense advantage of allowing the construction of area magic tori with easily quantifiable units, it also introduces the constraint of the tiling of the cells. It has been seen in the examples above that the PAMT can be represented as oblongs or as squares, while other irregular rectangular solutions also exist. A normal magic square of order-3 displays the numbers 1 to 9 and has a total of 45, which is not a perfect square. As the smallest addition to each of the nine numbers 1 to 9, in order to reach a perfect square total is four (45 + 9 ⋅ 4 = 81), this implies that when searching for a square PAMT with consecutive areas of 1 to 9, in theory the smallest polyominoes for this purpose will be pentominoes.

But to date, in the various shaped examples of PAMT shown above, the smallest cell area used to represent the area 1 is a tetromino, as this gives sufficient flexibility for the connections of a nine-cell PAMT of order-3 with consecutive areas of 1 to 9. Edo Timmermans has already constructed a Polyomino Area Magic Square of order-3 using pentominoes for the consecutive areas of 1 to 9, but it seems that such polyominoes cannot be used for the construction of a same-sized and shaped PAMT of order-3. Straight polyominoes are always used in the examples given above, as these facilitate long connections, but other polyomino shapes will in some cases be possible.

We should keep in mind that the PAMT are theoretical, in that, per se, they cannot tile a torus: As a consequence of Carl Friedrich Gauss's "Theorema Egregium", and because the Gaussian curvature of the torus is not always zero, there is no local isometry between the torus and a flat surface: We can't flatten a torus without distortion, which therefore makes a perfect map of that torus impossible. Although we can create conformal maps that preserve angles, these do not necessarily preserve lengths, and are not ideal for our purpose. And while two topological spheres are conformally equivalent, different topologies of tori can make these conformally distinct and lead to further mapping complications. For those wishing to know more, the paper by Professor John M. Sullivan, entitled "Conformal Tiling on a Torus", makes excellent reading.

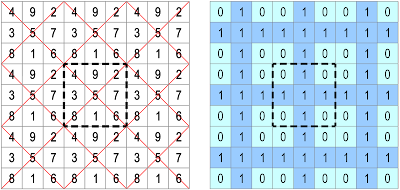
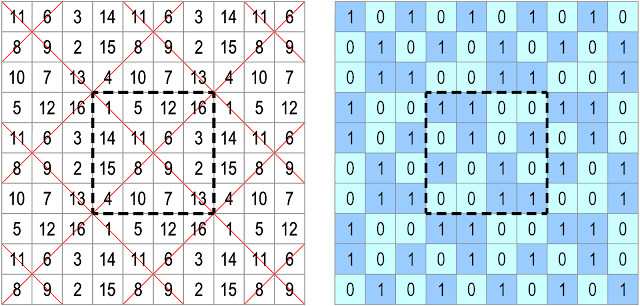
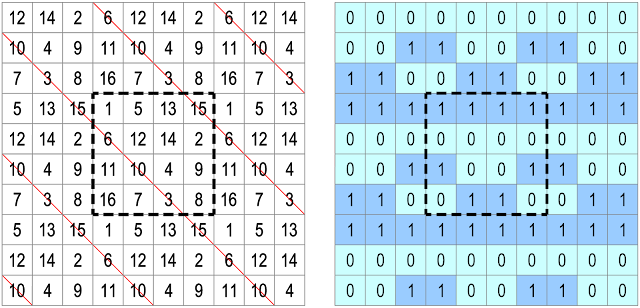
Notwithstanding their theoreticality, the PAMT nevertheless offer an interesting field of research that transcends the complications of tiling doubly-curved torus surfaces, while suggesting interesting patterns for planar tiling: For those who are not convinced by 9-colour tiling, 2-colour pandiagonal tiling can also be a good choice for geeky living spaces:

Tiling with irregular rectangular shaped PAMT of order-3. Monominoes. S=24.

Tiling with irregular rectangular shaped PAMT of order-3. Tetrominoes. S=15.

Tiling with irregular rectangular shaped PAMT of order-3. Trominoes. S=18.

Tiling with oblong PAMT of order-3. Trominoes. S=24.

Tiling with oblong pandiagonal PAMT of order-4. Pentominoes. S=34.

Tiling with oblong pandiagonal PAMT of order-5. Hexominoes. S=65.

Tiling with square pandiagonal PAMT of order-5. Monominoes. S=125.

Tiling with oblong partially pandiagonal PAMT of order-6. Heptominoes. S=111.

Tiling with square partially pandiagonal PAMT of order-6. Dominoes. S=147.

There are still plenty of other interesting PAMT that remain to be found, and I hope you will authorise me to publish or relay your future discoveries and suggestions!

Read more ...

How Dürer's "Melencolia I" is a painful but liberating metamorphosis!

The title of this post may at first seem rather strange, especially when we know that the main subjects of these pages are "Magic Squares, Spheres and Tori." However, the famous "Melencolia I" engraving by Albrecht Dürer does depict, amongst other symbols, a magic square of order-4 (already examined in "A Magic Square Tribute to Dürer, 500+ Years After Melencolia I," and "Pan-Zigzag Magic Tori Magnify the "Dürer" Magic Square"). 

In the section reserved for correspondence at the end of the post "A Magic Square Tribute to Dürer, 500+ Years After Melencolia I," I have recently received some interesting comments from Rob Sellars. Rob looks at Dürer's engraving from a Judaic point of view and describes the bat-like animal (at the top left) as a flying chimera which has a combination of the Tinshemet features of the "flying waterfowl and the earth mole." Rob's description has made me look harder at this beast, and in doing so, I have noticed some aspects that explain the very essence of "Melencolia I."

 

The Historical Context

The year 1514 CE came during a turbulent historical period, just three years before the Protestant Reformation, and the seemingly endless wars of religion which would follow. When Albrecht Dürer created "Melencolia I," he was expressing the philosophical, scientific, and humanist ideas of fifteenth-century Italy, and thus contributing to the beginning of a new phase of the Renaissance. Dürer was one of the first artists of Northern Europe to understand the importance of the Greek classics, and particularly the ideas of Plato and Socrates. The Renaissance idea was revolutionary, as it suggested that everyone was created "in imago Dei," in the image of God, and was capable of developing himself, or herself, to participate in the creation of the universe. This idea was now being gradually transmitted to all classes of society, thanks to the invention of the printing press; but it required a metaphorical language which could be deciphered by all, especially in a largely illiterate population. Although most of Dürer’s prints were intended for this wide public, his three master engravings (“Meisterstiche”), which include "Melencolia I," were aimed instead at a more discerning circle of fellow humanists and artists. The messages were more intellectual, using subtle symbols that would not be evident for common men, but could be decrypted by those initiated in the art.

The Metamorphosis of the Flying Creature

Detail of the bat-like beast at the top left-hand side of "Melencolia I" which was engraved by Albrecht Dürer in 1514

At first sight, the cartouche at the top left-hand side of Dürer's "Melencolia I" seems to be a flying bat, bearing the title of the engraving on its open wings. The length and thickness of the tail both look oversized, but we can suppose that Dürer was using his artistic licence to amplify the visual impact of the swooping beast. Nearly all species of bats have tails, even if most (if not all) of these, are shorter and thinner than the one that Dürer has depicted.

But looking again with more attention, we can see that, quite weirdly, the body of the animal is placed above its wings, which is impossible unless the bat is flying upside-down! Closer examination suggests that this is not the case, as the mouth and eyes of the beast are clearly those of an animal with an upright head. All the same, we might well ask where the hind feet are, and how the creature can possibly make a safe landing without these!

Looking once again more closely, we can see another, even more troubling detail, in that the “wings,” which carry the title of the engraving, are in fact two large strips of ragged skin, ripped outwards from the belly, as if the animal has disembowelled itself!

Judging from the thickness of its tail and the form of its head, the airborne creature was initially a rat before it began its painful metamorphosis. It has since carried out an auto-mutilation, and is now showing its inner melancholy to the outer world, but at the same time flying free with its hard-earned wings!

Symbolically, the cartouche is telling us that ""Melencolia I" is a painful metamorphosis which precedes a liberating "Renaissance!""

How Melancholy leads to Renaissance

During 1514 CE the artist's mother, Barbara Dürer (née Holper), passed away, or “died hard” as he described it, and we can therefore suppose that Dürer’s grief would have been a strong catalyst of the very melancholic atmosphere depicted in his “Melencolia I.” The melancholy, referred to in the title of the engraving, is illustrated by an extraordinary collection of symbols that fill the scene. Some of these are tools associated with craft and carpentry. Others are objects and instruments that refer to alchemy, geometry or mathematics. In addition to the bat-like beast, the sky also contains what might be a moonbow and a comet. Further symbols include a putto seated on a millstone, and a robust winged person, also seated, which could well be a metaphorical self-portrait. These, and many other symbols, are the object of multiple interpretations by various authors. Some scholars consider the engraving to be an allegory, which can be interpreted through the correct comprehension of the symbols, while others think that the ambiguity is intentional, and designed to resist complete interpretation. I tend to agree with the latter point of view, and think that the confusion symbolises the unfinished studies and works of the main melancholic figure; an apprentice angel, who believes that despite his worldly efforts, he lacks inspiration, and is not making sufficient progress.

Notwithstanding the melancholy that reigns, there is still hope: The 4 x 4 magic square, for example, has the same dimension as Agrippa's Jupiter square, a talisman that supposedly counters melancholy. The intent expression of the main winged person suggests a determination to overcome his doubts, and transcend the obstacles that continue to block his progression. Positive symbols of a resurrection or "Renaissance" are also plainly visible, not only in the hard-earned wings of the flying creature, but also in the growing wings that Dürer gives himself in his portrayal as the apprentice angel.

"Melencolia I" engraved by Albrecht Dürer in 1514

On page 171 of his book entitled "The Life and Art of Albrecht Dürer," Erwin Panofsky considers that "Melencolia I" is the spiritual self-portrait of the artist. There is indeed much resemblance between the features of the apprentice angel, and those of the engraver in previous self-portraits.

Dürer had already adopted a striking religious pose in his last declared self-portrait of 1500 CE, giving himself a strong resemblance to Christ by respecting the iconic pictorial conventions of the time. In other presumed self-portraits, (but not declared as such), Dürer had also presented himself in a Christic manner; in his c.1493 "Christ as a Man of Sorrows;" and in his 1503 "Head of the Dead Christ." What is more, Dürer inserted his self-portraits in altarpieces; in 1506 for the San Bartolomeo church in Venice ("Feast of Rose Garlands"); in 1509 for the Dominican Church in Frankfurt ("Heller Altarpiece"); and in 1511 for a Chapel in Nuremberg's "House of Twelve Brothers" ("Landauer Altarpiece" or "The Adoration of the Trinity"). Thus Dürer was already a master of religious self-portraiture when he engraved "Melencolia I" in 1514, and he might well have continued in the same manner. But this time, probably because the theological, philosophical and humanistic ideas of the Renaissance were not only spiritually, but also intellectually inspiring, he went even further, and gave himself wings!

Acknowledgement

Passages of "The Historical Context" are inspired by the writings of Bonnie James, in her excellent article "Albrecht Dürer: The Search for the Beautiful In a Time of Trials" (Fidelio Volume 14, Number 3, Fall 2005), a publication of the Schiller Institute.  

Latest Development

After reading this article, Miguel Angel Amela (who like me, is not only interested in magic squares, but also in "Melencolia I") sent me his thanks by email, and enclosed "a paper of 2020 about a painful love triangle..." His paper is entitled "A Hidden Love Story" and interprets the "portrait of a young woman with her hair done up," which was first painted by Albrecht Dürer in 1497, and then reproduced in an engraving by Wenceslaus Hollar, almost 150 years later in 1646. Miguel's story is captivating, and I wish to thank him for kindly authorising me to publish it here.

Read more ...

John Horton Conway and LUX

On the 25th April 2020, I came across a newsletter of the French magazine "Tangente" announcing that, despite the ongoing COVID-19 difficulties, their next issue n° 194 would still be published at the end of May. They stated that this future magazine would contain a main section dedicated to the late John Horton Conway, famous for his "Game of Life" (a cellular automaton in which cells live, die and are born). Having been previously unaware of Conway's death, I immediately wished to inform the fellow members of a magic square circle of the sad news, and sent them the following e-mail: 

Dear all,
I have just learnt that John Horton Conway passed away on the 11th April in New Brunswick, New Jersey, at the age of 82, after complications from COVID-19. I did not know him personally, but I expect that some of you did. His well-known LUX method for magic squares is an algorithm for creating magic squares of order 4n+2, where n is a natural number, and his "lozenge" method is another method of construction of magic squares. So this is a considerable loss to the magic square community, and goes to show that the virus is indiscriminate and dangerous.
Here's hoping that a cure will be found soon.
Stay safe!
William 

I rapidly received replies from Peter Loly, Bob Ziff, Awani Kumar and Miguel Angel Amela:

Peter Loly stated that Conway's passing away reminded him of his colleague Richard Guy who had passed away aged 103 on the 30th September 2019, and also of the losses of John Hendricks and Harvey Heinz, both of whom he had met. He asked if I could send this information out on the blog.

Bob Ziff replied to say that Conway had had the bad luck of being in a nursing home for some other health problems, and concluded by writing "Let’s all hope that we stay healthy!"

Awani Kumar replied with a simple "So sad. RIP."

Miguel Angel Amela then replied with a photomontage of a very fitting "in memoriam" plaque: He proposed that John Horton Conway's name could be inscribed above a 6x6 magic square constructed with Conway's LUX method, and that the Spanish words "descansa en la LUX" could be inscribed below. The Spanish text "descansa en la LUX" means "rest in the LUX" or "rest in the LIGHT." Miguel stated that in Latin, the inscription would be R.I.L. or "REQUIESCAT IN LUX," and he suggested a poem written by Art Durkee, entitled "requiescat in lux." 

An "In Memoriam" plaque for John Horton Conway

Adaptation of Miguel Angel Amela's idea of an "in memoriam" plaque for John Horton Conway

Perhaps, one day, a plaque like this will be placed at Cambridge or Princeton, or at another of Conway's haunts.

John Horton Conway's LUX Method

Martin Erickson has already described Conway's LUX method in page 98 of "Aha Solutions" (published by the Mathematical Association of America in 2009), and he even used the same "in memoriam" square of order-6 as a base array to construct a LUX square of order-18! However, here it is useful to examine how the LUX method can be used to construct the "in memoriam" square itself, and the following pdf file explains the construction steps:

The "in memoriam" magic square can also be programmed, for example using languages such as Elixir, Haskell and Ruby, as shown in "Magic squares of singly even order," edited by the programming chrestomathy site "Rosetta Code."

Conclusions

This short article only intends to commemorate a small part of John Horton Conway's work on magic squares. Because I myself have never had the pleasure of meeting him, those who did are far better placed to write about his other accomplishments, and about his life in general. The obituary written by Catherine Zandonella for Princeton University gives us a good insight, not only of his many achievements, but also of his mathematical playfulness and of his kind attention to others that made him many friends. Another source of information with useful external links is John Horton Conway's biography written by John Joseph O'Connor and Edmund Frederick Robertson for the MacTutor History of Mathematics Archive at the University of St Andrews. 

Acknowledgements

I wish to thank Peter Loly, Bob Ziff, Awani Kumar and Miguel Angel Amela for replying to my e-mail. Their messages and contributions have inspired me to write this post.

With COVID-19 still active and dangerous at the time of writing, I urge you all to take heed of the social distancing guidelines, and keep safe!

Read more ...

Even and Odd Number Patterns on Magic Tori of Orders 3 and 4

Ancient references to the pattern of even and odd numbers of the 3 × 3 magic square appear in the "I Ching" or "Yih King" (Book of Changes). In the introduction to the Chou edition, the scroll of the river Loh or "Loh-Shu", which is represented by the magic square of order-3, is written with black dots (the yin symbol and emblem of earth) for the even numbers, and white dots (the yang symbol and emblem of heaven) for the odd numbers. The "Loh-Shu" is incorporated in the writings of Ts'ai Yuän-Ting who lived from 1135 to 1198:

The Scroll of Loh, according to Ts'ai Yüang-Ting

A normal magic torus (or magic square) of order-n uses consecutive numbers from 1 to n² and consequently, for the order-3, the magic constant (MC) = 15. The Loh-Shu Magic Torus of Order-3 is presented below, together with its corresponding even and odd number pattern P3:

The "Loh-Shu" Magic Torus of Order-3 and its Even and Odd Number (x mod 2) Pattern P3

The magic torus T3 of order-3 is shown here as seen from the Scroll of Loh magic square viewpoint.

The even and odd number pattern P3 has reflection symmetry (with 6 lines of symmetry); rotational symmetry (of order 4); and point symmetry (over number 5, between numbers 3 and 7, between numbers 1 and 9, and between numbers 4, 6, 2, and 8).

The Even and Odd Number Patterns of the Magic Tori of Order-4

Only consecutively numbered magic tori (with numbers from 1 to n²) are studied here, and therefore, for order-4, the magic constant MC = 34.

The "Table of Fourth-Order Magic Tori" lists and describes each magic torus of order-4 using index numbers, while "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus" gives a group categorisation of the magic tori of order-4 using type numbers. Both of these classifications give the details of the Frénicle indexed magic squares that are displayed by each torus.

In the study that follows it can be seen that there are 4 essentially different even and odd number patterns on the magic tori of order-4:

The Order-4 Even and Odd Number Pattern P4.1
(represented by the pandiagonal torus T4.198)

The Pandiagonal Torus T4.198 of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.1

The pandiagonal torus of order-4 (with index n° T4.198 and type n° T4.01.2) is shown here as seen from the Frénicle n° 107 magic square viewpoint.

The even and odd number pattern P4.1 has reflection symmetry (with 6 lines of symmetry); rotational symmetry (of order 2); and multiple point symmetry when reading as a torus. The pattern P4.1 also has negative symmetry (evens to odds and vice versa).

The even and odd number pattern P4.1 concerns 79 out of the 255 magic tori, and 404 out of the 880 magic squares of order-4. These include the 3 pandiagonal tori that display 48 pandiagonal squares; 30 semi-pandiagonal tori that display 240 semi-pandiagonal squares; 12 partially pandiagonal tori that display 48 partially pandiagonal squares; and also 34 basic magic tori that display 68 basic magic squares.

The Order-4 Even and Odd Number Pattern P4.2
(represented by the semi-pandiagonal torus T4.059)

The Semi-Pandiagonal Torus T4.059 of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.2

The semi-pandiagonal torus of order-4 (with index n° T4.059 and type n° T4.02.2.01) is shown here as seen from the Frénicle n° 21 magic square viewpoint.

The even and odd number pattern P4.2 has reflection symmetry (with 8 lines of symmetry); rotational symmetry (of order 4); and multiple point symmetry when reading as a torus. The pattern P4.2 also has negative symmetry (evens to odds and vice versa).

The even and odd number pattern P4.2 concerns 72 out of the 255 magic tori, and 256 out of the 880 magic squares of order-4. These include 18 semi-pandiagonal tori that display 144 semi-pandiagonal squares; 6 partially pandiagonal tori that display 16 partially pandiagonal squares; and also 48 basic magic tori that display 96 basic magic squares.

The Order-4 Even and Odd Number Pattern P4.3
(represented by the partially pandiagonal torus T4.186)

The Partially Pandiagonal Torus T4.186 of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.3

The partially pandiagonal torus (with index n° T4.186 and type n° T4.03.1.3) is shown here as seen from the Frénicle n° 100 magic square viewpoint.

The even and odd number pattern P4.3 has reflection symmetry (with 8 lines of symmetry); rotational symmetry (of order 4); and multiple point symmetry when reading as a torus. The pattern P4.3 also has negative symmetry (evens to odds and vice versa).

The even and odd number pattern P4.3 concerns 16 out of the 255 magic tori, and 44 out of the 880 magic squares of order-4. These include 6 partially pandiagonal tori that display 24 partially pandiagonal squares; and also 10 basic magic tori that display 20 basic magic squares.

The Order-4 Even and Odd Number Pattern P4.4
(represented by the basic magic torus T4.062)

The Basic Magic Torus T4.062 of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.4

The basic magic torus (with index n° T4.062 and type n° T4.05.1.12) is shown here as seen from the Frénicle n° 37 magic square viewpoint.

The even and odd number pattern P4.4 has reflection symmetry (with 8 lines of symmetry); rotational symmetry (of order 2); and multiple point symmetry when reading as a torus. The pattern P4.4 also has negative symmetry (evens to odds and vice versa).

The even and odd number pattern P4.4 concerns 88 out of the 255 magic tori, and 176 out of the 880 magic squares of order-4. All of these 88 magic tori and the displayed 176 magic squares are basic magic.

Observations on the Even and Odd Number Patterns of the Magic Tori and Magic Squares of Order-4

The findings of the even and odd number patterns of the magic tori of order-4 are recapitulated and analysed in comparative tables, (together with the Dudeney complementary number patterns and the Magic Torus self-complementary and paired complementary number patterns), in the file below:

The Even and Odd Number Patterns of the Semi-Magic Tori of Order-4

Only consecutively numbered semi-magic tori (with numbers from 1 to n²) are studied here, and consequently, for the order-4, the magic constant MC = 34.

In "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus" the 4,038 semi-magic tori of order-4 have been sorted, and type numbers have been attributed taking into account the arrangements of their magic diagonals (if any). 

Each of the four even and odd number patterns already found above on the magic tori of order-4, also occur on semi-magic tori of order-4. For example, from left to right below, we find a semi-magic torus type T4.08.0W with pattern P4.1; a semi-magic torus type T4.08.0X with pattern P4.2; a semi-magic torus type T4.07.0Y with pattern P4.3; and a semi-magic torus type T4.09.00Z with pattern P4.4:

Semi-Magic Tori of Order-4 with Even and Odd Number (x mod 2) Patterns P4.1, P4.2, P4.3 and P4.4

The even and odd number patterns P4.1 to P4.4 are not the only ones that can be found, but the patterns which are specific to the semi-magic tori of order-4 have neither been fully investigated nor precisely counted, and the examples that follow only represent some of the different varieties.

The Order-4 Even and Odd Number Pattern P4.5
(represented by the semi-magic torus type T4.06.0A)

The Semi-Magic Torus type T4.06.0A of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.5

This semi-magic torus type n° T4.06.0A was found by Walter Trump, and has been previously illustrated in "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus".

The even and odd number pattern P4.5 has diagonal reflection symmetry (with 4 lines of symmetry); and negative (evens to odds and vice versa) rotational symmetry (of order 2). The blocks of even and odd numbers are translations of each other.

The Order-4 Even and Odd Number Pattern P4.6
(represented by the semi-magic torus type T4.07.0A)

The Semi-Magic Torus type T4.07.0A of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.6

This semi-magic torus type n° T4.07.0A was found by Walter Trump, and has been previously illustrated in "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus".

The even and odd number pattern P4.6 has reflection symmetry (with 4 lines of symmetry); rotational symmetry (of order 2); and multiple point symmetry when reading as a torus. The blocks of even and odd numbers are translations of each other.

The Order-4 Even and Odd Number Pattern P4.7
(represented by the semi-magic torus type T4.09.00M)

The Semi-Magic Torus type T4.09.00M of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.7

This semi-magic torus type n° T4.09.00M was found by Walter Trump, and has been previously illustrated in "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus".

The even and odd number pattern P4.7 has both positive and negative reflection symmetry; negative rotational symmetry (of order 2); and multiple negative point symmetry when reading as a torus. The blocks of even and odd numbers are translations of each other.

The Order-4 Even and Odd Number Pattern P4.8
(represented by the semi-magic torus type T4.10.000X)

The Semi-Magic Torus type T4.10.000X of Order-4 and its Even and Odd Number (x mod 2) Pattern P4.8

3,726 semi-magic tori of the type 10 have been found by Walter Trump, and his findings are detailed in "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus".

The T4.10.000X's even and odd number pattern P4.8 has negative reflection symmetry (2 lines of symmetry); negative rotational symmetry (of order 2); and multiple point symmetry when reading as a torus. The blocks of even and odd numbers are translations of each other.

General Observations

The "Table of Fourth-Order Magic Tori" has been revised to include the even and odd number pattern references for each of the magic tori of order-4 (listed together with the Frénicle indexed magic squares that each magic torus displays).

Other interesting websites that examine, but do not enumerate, the different even and odd number patterns on magic squares of order-4, include "4x4 Magic Squares" by Dan Rhett and "Pattern in Magic Squares" by Vipul Chaskar.

A brief look at higher-orders suggests that the order-5 has many irregular patterns; the order-6 has many patterns with negative reflection symmetry (evens to odds and vice versa); the order-7 has many patterns with rotational symmetry; and the order-8 has patterns very like those of the order-4 examined above. All of these orders merit an in-depth analysis of their even and odd number patterns.

In conclusion, it is interesting to note that the Arab mathematicians of the tenth century constructed odd-order magic squares with striking even and odd number patterns (as for example the magic squares in figures b44 and b49 on pages 243 and 248 of Magic Squares in the Tenth Century: Two Arabic treatises by Anṭākī and Būzjānī, translated by Jacques Sesiano). And in the same context, Paul Michelet has recently brought to my attention a magnificent 15 x 15 magic square by Ali b. Ahmad al-Anṭākī (d. 987). Al-Anṭākī's bordered magic square is solid evidence of the Middle Eastern mathematicians' mastery of even and odd number patterns!

Read more ...