 |
Today, when searching on Internet for "magic cubes," we will most likely be directed towards sites about "Rubik's Cubes." This state of affairs results from a certain indifference for the mathematics, which though essential for the creation of that puzzle, was rapidly forgotten during the recreations! Despite the improbability of an equal interest for the mathematics as there is for the game, how can we reduce the "Like" gap between the two, and boost the rating of the mathematical magic cubes?
It is hardly a coincidence that, a year after his 1974 invention, Ernő Rubik then filed for a Hungarian patent of a “Bűvös kocka,” or "Magic Cube." The patent was granted in 1977, but when Ideal Toy Company bought exclusive rights in 1979, they decided, for trademark protection reasons, to opt for the name "Rubik's Cube." Perhaps this year 2024, which marks the 50th anniversary of the puzzle, will kindle new interest in the "Magic Cube" that Rubik was thinking about.
History of Magic Cubes
Jacques Sesiano has pointed out, in his paper entitled "The First Appearance of Magic Cubes," that 12th-century Persian examples, created by Abdarraḥmān al-Khāzinī, did not obey the same definitions as today. Therefore, the generally-accepted earliest-known magic cube was an order 4 example, that was first sent by Pierre de Fermat to Marin Mersenne on the 1st April 1640, before being published by Édouard Lucas in his 1895 book entitled "L'Arithmétique Amusante." Also, back in 1833, Ferdinand Julius Brede, alias "de Fibre", was the first to publish a perfect magic cube, which was of order 7, in the volume 3, issues n° 4 and following, of "Iduna," a discrete German magazine, which Google has translated as being "for youth of both sexes, with instructive, amusing and spiritually stimulating content". Perhaps it was because the cube was published in weekly instalments, and via such an unusual media, that Brede's achievement seems to have either passed unnoticed, or been completely forgotten by mathematicians. In fact, it has only recently been unearthed by Holger Becker and Walter Trump, who have reannounced it in their 2024 paper, "New Discoveries in the History of Magic Cubes."
Martin Gardner has retraced more history of magic cubes, in chapter seventeen of his book, published in 1988, and entitled "Time Travel and Other Mathematical Bewilderments." There have been new developments since, and these are discussed by authors such as: Christian Boyer in his page "Perfect Magic Cubes" from Multimagic Squares; Dwane H. Campbell in his page "Magic Cubes" from Magic Tesseract; Bogdan Golunski in his Magic Cube pages from Number Galaxy; Harvey D. Heinz in his page "Magic Cubes - Introduction" from Magic Stars & Other Patterns; Walter Trump, in his page "Perfect Magic Cubes" from Notes on Magic Squares and Cubes; and Aale de Winkel in his page "The Magic Encyclopedia DataBase" from The Magic Encyclopedia. Please note that this list is inevitably incomplete, and that there are many other authors who have contributed important studies of the subject in question.
Incompatibilities of Magic Cubes with Rubik's Cubes or with other Twisty Puzzles, and a Possible Resolution?
The main thing to notice about magic cubes of order n is that, when physically constructed in 3D, they are "solid" n x n x n arrays of blocks, or cubelets, which are normally numbered from 1 to n³. In consequence, traditional magic cubes like this are incompatible with Rubik's Cubes and other twisty puzzles, as these have central mechanisms, and can only accommodate the outer cubelets.
The purpose of the present article is therefore to propose "hollow" magic box cubes that will be coherent with Rubik's Cubes and other twisty puzzles, such as, ( for example), the V-cube, invented by Panagiotis Verdes.
Comparison of the Properties of Magic Cubes and Magic Box Cubes
At this point, it is useful to compare the properties of traditional magic cubes with those of the proposed magic box cubes:
The Quantity Qₙ of the entry blocks, or cubelets, per order n:
For Magic Cubes, Qₙ = n³
For Magic Box Cubes, Qₙ = 6n² - 12n + 8
The Total Tn of consecutive entries from 1 to Qₙ:
For Magic Cubes, Tₙ = (n³ (n³ + 1)) / 2
For Magic Box Cubes, Tₙ = (3n² - 6n + 4) (6n² - 12n + 9)
The Magic Constant Cₙ (for all orthogonal lines, and in some cases for diagonal lines):
For Magic Cubes, Cₙ = (n (n³ + 1)) / 2
For Magic Box Cubes, Cₙ = (n (6n² - 12n + 9)) / 2
Fuller details, together with lists of the data per order, are given in "Properties of Magic Box Cubes," enclosed below:
Comparison of the Definitions of Magic Cubes and Magic Box Cubes
According to Martin Gardner's above-mentioned book, a "perfect magic cube" is a cubic array of positive integers from 1 to n³ such that every straight line of n cells adds up to a constant. These lines include all of the orthogonals (the lines that are parallel with an edge), the two main diagonals of every orthogonal cross section, and the four space diagonals (also called triagonals). We notice that the magic diagonals of the faces are not mentioned. The definitions of traditional magic cubes have since been relaxed to include a "semiperfect magic cube" where only the orthogonals and the space diagonals are obligatorily magic, thus admitting the existence of magic cubes in lower orders (when n = 3 or 4).
We have already seen in "Properties of Magic Box Cubes" that "normal" versions of these do not exist in order 3, or in other odd orders for that matter. We are also aware of the proof, given by Richard Schroeppel, of the non-existence of any traditional perfect magic cubes of order 4, that was published in February 1972 in "Artificial Intelligence Memo 239," (in HAKMEM Item 50, of the Massachusetts Institute of Technology). However, Schroeppel's proof, which takes into account oblique magic squares, cannot be generalised for magic box cubes.
The proposed magic box cubes, which can only exist in even orders, have neither orthogonal magic cross sections, nor space diagonals (otherwise called triagonals). The closest equivalent of a "perfect magic cube", of even order n, is therefore, for box cubes, a pandiagonal cubic array of positive integers from 1 to (n³ - (n - 2)³) such that every straight line of n cells adds up to a constant. These lines include all of the orthogonals (the lines that are parallel with an edge), and also the main and broken diagonals of each of the six faces. Pandiagonal magic box cubes remain to be found in order 4, and might only be possible from order 8 upwards; as although non-normal pandiagonal squares exist in order 6, it will be difficult to find any that can satisfy the constraints.
In all even orders n > 2, it will always be easier to either construct a non-pandiagonal, but "diagonally magic box cube", where each of the 6 faces displays magic squares; or build an "orthogonally magic box cube," with < 6 magic square faces. Similarly to "normal" magic cubes, which cannot display "normal" magic squares or "normal" semi-magic squares, the same applies to "normal" magic magic box cubes. This is because, on normal magic cubes or box cubes, their magic or semi-magic squares can never be entirely constituted of consecutive numbers.
Higher degrees of perfection can be reached, if the magic box cubes are associated (centrosymmetric), or if they possess other special qualities (such as the bordered diagonal magic cube of order 16, which was found by Mitsutoshi Nakamura in 2004). All of these definitions can yet evolve, depending on future findings.
Magic Box Cubes of Order 3
A Magic Box Cube of Order 3, that is Orthogonally Magic but "Non-Normal"
Although "normal" magic box cubes, with consecutive numbers, cannot exist in odd orders, the study would be incomplete without a proposition for the original 3x3x3 Rubik's Cube!
The example below is inspired by a traditional magic cube, first discussed by William Symes Andrews, in his paper "Magic Cubes," that was published in The Monist, Vol. 16, No. 3 (July, 1906), pp. 388-414. Illustrated in fig. 10 of Andrews's essay, it is one of four possible solutions for a magic cube of order 3, and the example chosen by John R. Hendricks for his paper entitled "The Five and Six Dimensional Magic Hypercubes of Order 3 (received February 1, 1962)," published by the Canadian Mathematical Bulletin in 1962. As these magic cubes were first published before the 1st January, 1929, they have since made their way into the public domain.
 |
| A Perspective of a Magic Box Cube of Order 3 - Version 1/4 |
The traditional magic cube of order 3 has 27 consecutive numbers 1 to 27, and a magic constant of 42. In each of the four versions found by Andrews, the number 14 is at the centre. With 14 in this central position, all of the internal orthogonals and cross-section diagonals also have the magic constant of 42. In the illustration above, the non-normal magic box cube of order 3 has 26 cubelets that are consecutively numbered from 1 to 13, and from 15 to 27. But as the magic constant of 42 remains unchanged, the number 14 has invisibly disappeared: It's magic!
 |
| Plans and elevations of a Magic Box Cube of order 3 - Version 1/4 |
 |
| Net Diagram 1 of a Magic Box Cube of order 3 - Version 1/4 |
Please note that although the net diagram 1 has the advantage of highlighting the cubic patterns of the evens and odds, it would be advisable to use the net diagram 2 when constructing a 3D model of the magic box cube: The second net diagram will allow for better-aligned numbers.
 |
| Net Diagram 2 of a Magic Box Cube of order 3 - Version 1/4 |
Compatibility of Magic Box Cubes of Order 3 with the Rubik's Cube and other Twisty Puzzles
The archetypal Rubik's Cube 3x3x3 was invented in 1974 by Ernő Rubik, and originally called "Magic Cube." But following the purchase of the exclusive rights by Ideal Toy Company in 1979, and for trademark protection reasons, the puzzle was then renamed after its creator. Subsequently to its resale in 2021, the Rubik's brand, formed around the Rubik's Cube and other puzzles, now belongs to a Canadian company, Spin master. Since it's creation, the famous cube has inspired many variations, which have, more often than not, been designed and patented by others.
The Rubik's Cube 3x3x3 has 43,252, 003,274,489,856,000 possible permutations, which makes it very challenging. Thanks to the efforts of Thomas Rokiki, Herbert Kociemba, Morley Davidson, and John Dethridge, who used a Google donation of about 35 CPU-years of calculations, God's Number, which is the smallest number of moves needed to solve the puzzle from any starting position, has since July 2010, been determined to be 20. One of the most famous scrambled positions that require exactly 20 moves to solve the puzzle, is now called the Super Flip. The entire research, described in a paper entitled "The Diameter of the Rubik's Cube Group is Twenty," is published by the SIAM Society for Industrial and Applied Mathematics in its Journal on Discrete Mathematics, Vol. 27, No. 2 (2013), pp. 1082-1105.
Each of the four non-normal magic box cubes of order 3 is compatible with the Rubik's Cube 3x3x3, but concerning the cubelets of the latter, we know that corners will always be corners; edges will always be edges; and fixed faces will always be fixed faces. Therefore, because each of the four versions of the magic box cube of order 3 would require different numbers to be allocated to the key pieces, there is a dilemma, as it would be impossible to migrate from one solved state to another - even by disassembly. It will be necessary to choose, and the version 1, with its number 1 on a corner cubelet, was the candidate selected above. On the other hand, it would be nice to have a full set of the four puzzles, and play, either alternatively with each, or simultaneously with all! So here are the "Four Essentially Different, Non-Normal Magic Box Cubes of Order 3," in case you would like to compare them and make your own choice:
The objective of a magic box cube puzzle of order 3 would simply be to return it to its solved state after scrambling. The colour scheme of the magic box cube is indicative, and the general question of colours is discussed separately at the end of this study.
Other Possibilities with Non-Normal Magic Box Cubes of Order 3
Unless we adopt other "non-normal" magic box cubes, with different numbering constraints, that might include prime-numbered examples, there are no other solutions in order 3. In 1977, Akio Suzuki, (who, according to Mutsumi Suzuki, replying to a question from Carlos Rivera was "an amateur (not mathematicain [sic] but an owner of now old book shop)"), found a minimally-sized associative magic cube of prime numbers of order 3. Traditionally constructed, with the central core that does not exist in magic box cubes, Suzuki's prime-numbered order 3 cube has a magic constant of 3309. Harvey Denis Heinz wrote in his page entitled "Prime Number Magic Cubes," that after a computer search in 2003, Allan Wm. Johnston, Jr. confirmed that the cube had "the smallest possible sum for an order 3 prime magic cube using distinct digits." Although Akio Suzuki's prime magic cube is not illustrated here, it should nevertheless inspire the creation of magic box cubes of primes; and if possible, examples without the central number!
Magic Box Cubes of Order 4
A Magic Box Cube of Order 4, which is not only Diagonally Magic, but also Half Semi-Pandiagonal
In September 1979, Thomas Krijgsman found a very impressive, nearly perfect magic cube of order 4, which was later published in March 1982 in an article entitled "De toverkubus van Krijgsman" on page 109 of Pythagoras 5, Jaargang 21. At the time of writing, it is also on the Wikipedia page "Perfect Magic Cube," which can seem strange, as we already know that there are no perfect magic cubes of order 4. Traditional magic cube definitions can become blurred, depending on the evolution of classification methods, and different points of view concerning the terminology. However, each of Krijgsman's cube's 12 orthogonal planes displayed a non-normal magic square (with non-consecutive numbers), and all of the lines had magic constants of 130, except for certain broken diagonals and the 4 space diagonals (or triagonals). Then, on the 2nd January 2004, Walter Trump found a nearly perfect magic cube of order 4 which though constructed differently, with complementary pairs, was otherwise similarly magic. Shortly after this discovery, Trump's cube was published in an article by Dr. Christoph Pöppe entitled "Perfekte magische Würfel" on pages 108-110 of the March 2004 edition of "Spectrum der Wissenschaft", the German version of Scientific American.
By circumventing the space diagonals (or triagonals), and thus avoiding the oblique magic squares that would have otherwise been implied by the diagonals of surface-magic squares, both Krijgsman's and Trump's nearly perfect magic cubes of order 4 were liberated from the constraints of Schroeppel's proof, and were able to show non-normal surface-magic squares on each of their 6 faces. Krijgsman's and Trump's achievements are equally-inspiring, but the following magic box cube is more influenced by Trump's example, as like his, it also uses complementary pairs.
Due to the fact that magic box cubes do not have internal numbers, there are neither orthogonal magic cross sections, nor space diagonals (otherwise called triagonals). The magic box cube is a surface-magic layer that envelops a cubic space, and this is why adjectives such as "perfect magic" or "nearly perfect magic" no longer seem applicable, while others such as "diagonally magic" or "orthogonally magic" seem more appropriate.
In the following illustration of a diagonally magic box cube of order 4, each of the 6 faces displays a non-normal magic square, and 3 of these are semi-pandiagonal. All of the lines have magic constants of 114, except for certain broken diagonals:
 |
| Perspective of a Diagonally Magic Box Cube of Order 4 |
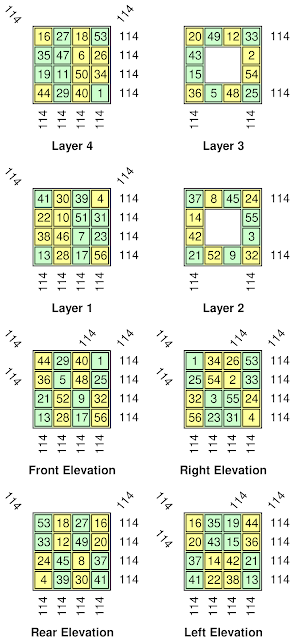 |
| Plans and elevations of a Diagonally Magic Box Cube of order 4 |
Traditional magic cubes of order n are often described with separate plans of each of their different layers from 1 to n. We can do the same for the proposed magic box cubes, but for these we also have the possibility of using alternative net diagrams. Please note that although a diagram like this can describe any magic box cube, care should be taken when reading it: Unlike the layer plans, where every number appears only once; on net diagrams, such as the one below, the edge numbers always appear twice, and the corner numbers thrice:
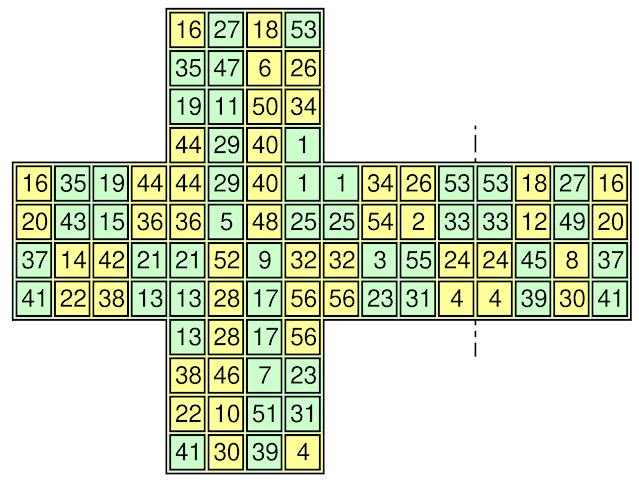 |
| Net Diagram of a Diagonally Magic Box Cube of Order 4 |
If assembly tabs are added, this net diagram can easily be cut out and pasted, to construct a 3D model of the diagonally magic box cube. This type of net diagram is one of the best-known ways of folding the cube, but there are 11 different methods: For more information, there is a Wolfram demonstration project, contributed by Izidor Hafner and entitled "All 11 Folding Nets of the Cube."
Other Magic Box Cubes of Order 4, including Four Variants that are directly related to the Diagonally Magic solution - all Sorted by Similarly-Numbered Cubelet Types
 |
| Diagonally Magic Box Cube of Order 4 in its original solved state - D1.0 |
If the diagonally magic box cube, previously illustrated and discussed above, is here renamed as the version D1.0, so as to mean the original & solved state of a twisty puzzle, it is interesting to observe that, after scrambling, several other essentially-different diagonally magic examples can be found. Occasionally these have rotated numbers, but they nevertheless remain valid diagonally magic box cubes. Here are just four of the many cases that players might come across while making their moves:
 |
| Diagonally Magic Box Cube of Order 4 - D.1.1 |
 |
| Diagonally Magic Box Cube of Order 4 - D1.2 |
 | |
| Diagonally Magic Box Cube of Order 4 - D1.3 |
 |
| Diagonally Magic Box Cube of Order 4 - D1.4 |
To see additional details of these four variants, and for more information about other orthogonally magic box cubes, please refer to "Examples of Magic Box Cubes of Order 4 Sorted by Similarly-Numbered Cubelet Types," enclosed below:
Compatibility of Magic Box Cubes of Order 4 with the Rubik's Revenge and other Twisty Puzzles
All of the magic box cubes of order 4 are compatible with the Puzzle Cube 4x4x4, that was first released in 1981, and relies on a mechanism which was not invented by Ernő Rubik, but by Péter Sebestény. The latter subsequently sold the rights to the Rubik's Brand (then owned by Ideal Toy Company), and these have since been purchased by Spin Master. A Taiwanese manufacturer, East Sheen Industrial Co., Ltd. also fabricates "Eastsheen" 4x4x4 cubes, that have similarities to the original, but are supposedly of a higher quality, moving faster and smoother. Other manufacturers include the Chinese company ShengShou.
As with all even-order Rubik's Cubes, the central face cubelets of the Rubik's Revenge can move around and cannot be immediately used as a reference point for solving the cube. However, this added liberty of movement has the advantage of allowing players to discover other diagonally or orthogonally magic solutions, while they make their sequences of moves towards a diagonally magic solved state.
According to "The Cubic Circular," Issues 3 & 4, published by David Singmaster in 1982, the total number of possible permutations of a Rubik's Revenge 4³ is:
7, 401,196,841,564,901, 869,874,093,974,498, 574,336,000,000,000 = 7.4 × 10⁴⁵.
Other Non-Normal Magic Box Cubes of Order 4
Like the possibility discussed in order 3, non-normal magic box cubes of order 4 could include prime-numbered examples, which might be inspired by Natalia Makarova's minimally-sized associative magic cube. Traditionally constructed, with a central core that does not exist in magic box cubes, Makarova's prime-numbered order 4 example has a magic constant of 1260.
Magic Box Cubes of Order 6
A Magic Box Cube of Order 6, which is Diagonally Magic
The example below, was inspired by a traditional perfect magic cube of order 6, which was found by Walter Trump on the 1st September 2003. Each of Trump's cube's orthogonal planes, was a non-normal magic square (with non-consecutive numbers). All of the lines had magic constants of 651, except for the broken diagonals, and there were a total of 36 magic diagonals plus 4 space diagonals (also called triagonals).
Here, a diagonally-magic box cube of order 6 is represented firstly by a perspective view, secondly by its 6 faces, and thirdly by a net diagram. The four intermediate layers 2 to 5 are not shown, but they can easily be deduced when observing the elevations or the net diagram. All of the orthogonal lines have magic constants of 459, and each of the magic box cube's faces have main diagonals that are magic:
 |
| The 6 faces of a Diagonally Magic Box Cube of order 6 |
 |
| Net Diagram of a Diagonally Magic Box Cube of Order 6, displaying 6 Magic Squares |
Compatibility of Magic Box Cubes of Order 6 with Twisty Puzzles such as V-Cubes
All magic box cubes of order 6 are compatible with the Puzzle Cube 6x6x6, which relies on a mechanism that was invented by Panagiotis Verdes and patented by V-cube in 2004. Manufactured since the beginning by V-Cube, the "V-Cube 6" has lead to various adaptations that are now mass-produced by several other Chinese companies, including YongJun YJ, QiYi Toys, MoYu and ShengShou. Although it was originally inspired by the Rubik's Cube, the Puzzle Cube 6x6x6 is neither manufactured by, nor related to the Rubik's brand.
As with all even-order Rubik's Cubes and twisty puzzles, the central face cubelets can move around, thus preventing their immediate use as a reference point for solving the cube. However, as already mentioned for the order 4, this freedom of movement allows the discovery of alternative orthogonally or diagonally magic solutions, while making the sequences of moves towards a predetermined diagonally magic solved state.
According to calculations by Jaap Scherphuis, the number of positions of a 6x6x6 V-cube is:
7!𑁦24!⁶𑁦3⁶ / 4!²⁴ = 157,152,858,401, 024,063,281,013,959, 519,483,771,508,510, 790,313,968,742,344, 694,684,829,502,629, 887,168,573,442,107, 637,760,000,000,000, 000,000,000,000,000 = 1.57𑁦10¹¹⁶ positions.
Adaptations of Rubik's Cubes and other Twisty Puzzles for Magic Box Cubes
How Sudoku Cubes are Different from Magic Box Cubes
A numbered Sudoku puzzle already exists on Rubik's Cubes, and on other twisty puzzles. In 2006, the "Sudoku Cube," a variation of the Rubik's Cube, was created by Jay Horowitz, the owner of Ideal Toy Company. The product is made in China by American Classic Toy Inc., which Horowitz also founded. The U.S. patent for the Sudoku Cube, which was granted in 2010, states that either single-digit numbers are to be used, or any other type of unique indicia; and that a solved condition is one that avoids duplicates on same columns or rows, of one or more faces of the cube. In the illustrations of the patent, we notice that the corners and edges do not always display a same number. The success of the Sudoku Cube has incited competition, and other versions such as "Sudokube" have appeared. Today, Sudoko 3D games are also available on several platforms, mobile apps and desktop applications.
At the time of writing, the Speed Cube Shop proposes different versions of Sudoku Cubes 4x4x4, with 4, 8 or 16 colours; the goal being to scramble the cube and then return it to its original state. The 4 and 8 colour versions, which allow for solid-colour corners and edges, are interesting, as these could express the underlying structure of magic box cubes. However, any comparison ends there, as there are no inscriptions of the numbers from 1 to (n³ - (n - 2)³), which, for order 4, would imply cubelets numbered from 1 to 56. Again at the time of writing: The Cubicle proposes a Sudoku Cube 3x3 V6 (Ultra), manufactured by Calvin's Puzzle, and similar in style to the example shown above. This too, is one of a range of stickerless cubes with aesthetic solid-colour corners and edges, available in a choice of colour schemes, but once more without any numbering.
How Home-Made Stickers would be a Simple but Non-Ideal Solution
A simple way of implementing the ideas of magic box cubes on Rubik's Cubes, and on their variations, would be to affix number stickers to the faces of their cubelets. These stickers could either be home-designed and made with a custom sticker kit and a printer, or eventually, in the future, custom-ordered from a professional sticker manufacturer. However solutions like this would not be ideal, as with time, stickers can fade and peel.
Constraints of Permutations on Rubik's Cubes and other Twisty Puzzles
Wrapped around the core mechanisms, of Rubik's Cubes or of other twisty puzzles, there are 3 types of surface cubelets:
1) Firstly there are the corner cubelets which have 3 visible sides, and 3 valid orientations for each of the possible positions.
2) Secondly there are the edge cubelets which have 2 visible sides, and 2 valid orientations for each of the possible positions.
3) Thirdly there are the face cubelets which have 1 visible side, and, in even orders, are free to move to different positions. In odd orders the centremost face cubelet is always fixed to the mechanism of the cube, but for odd orders n > 3, the other-than-central face cubelets are free to move around.
It is important to note that: corners will always be corners; edges will always be edges; and faces will always be faces. These are the practical constraints on the possible permutations on a Rubik's Cube or on other twisty puzzles. However, in eventual mobile apps, desktop applications, or online simulators with head-mounted displays (HMDs), virtual reality magic box cubes could be designed to allow a choice of; either the same permutation constraints as those of the physical cubes; or an increased liberty of the rotational movements.
For readers interested by the group theory of the Rubik's Cube group, much of the available information only concerns the 3x3x3 Rubik's Cube. However, there are some studies that examine even order twisty puzzles, such as, for example, the paper "Analyzing the Rubik's Cube Group of Various Sizes and Solution Methods," by Alexander Chuang.
Implementations of Magic Box Cubes on Rubik's Cubes and on other Twisty Puzzles
We have already observed that orthogonally magic box cubes of order 3 can be adapted, and that diagonally magic box cubes of orders 4 and 6 are compatible with Rubik's Cubes and their variations. Now it is useful to determine the practicalities, in order to optimise the eventual implementations.
In standard practice, after scrambling, the solved state of a twisty puzzle is achieved when each of the cube's faces is totally covered by one of the six standard colours, (or five standard colours; white being achromatic). The magic box cube numbering could therefore simply be applied to cubes that are coloured that way; creating no further difficulty in the reassembly, but just informing the player about the magic solution. In 2024, Christopher Wanamaker adapted a 3x3x3 Rubik's Cube photo by Justus Menke, to show an order 3 magic cube, but did not mention a missing number 14. Wanamaker's illustration appears above a "HubPages" article, entitled "Exploring the History and Mystery of Magic Squares, Cubes, and Beyond." However, with a standard colour approach like this, there would be nothing new to resolve:
The main interest of an eventual magic box cube twisty puzzle will be in its magic line construction, which should arouse the curiosity of potential players, and incite them to rise to the challenge. For orders n > 3, an added incentive would be the the possible discovery of other magic solutions, either during the players' series of moves towards a solved state, or during their numerical explorations﹘just for the fun of it. Without standard colouring to assist the orientation, players would need to rely on mental arithmetic, and mathematical logic: For example, sometimes, but not always, the cubelets are arranged by complementary pairs, and this would help the players to find solutions. However, in order 4, the magic constant of a magic box cube is already 114, and this sum continues to rise exponentially in higher orders. So although some all-white cubes have already been suggested, it would also make sense to systematically propose alternative coloured cubes which can be of use to the player. This could be with two colours, either representing the evens and the odds, or eventually representing the integers that are greater-than, or less-than-or-equal-to the mean of the highest consecutive number of even orders. The bicolour perspectives that have been proposed so far, use pastel colours. But should brighter colours be considered more ludic, a bicolour magic box cube might look more like this:
 |
| A Brighter Colour Perspective of a Magic Box Cube of Order 3 - Version 1/4 |
We should not forget the fact that the World Cube Association has regulations for their cubing events which state in their article 3a3, that "polyhedral puzzles must use a color scheme with one unique color per face in the solved state." This would of course disqualify any even-odd colour scheme in official competitions sanctioned by the WCA, unless the rules were to be adapted to allow for bicolour magic box cubes.
If implemented in a logical manner, palettes with more than two colours could give extra help to the players, but at the risk of distracting their attention from the numbers. However, if downloadable mobile apps, desktop applications, or online games were to be developed for magic box cubes, it would be a good idea to let the players choose their preferred colour schemes.
Ideally, in a deluxe version of a magic box cube, either on a Rubik's Cube, or on another twisty puzzle, no colours of any sort would be necessary; but if it is technically possible, any magic line should automatically light up and any diagonal magic line should be accentuated by an extra lighting effect. This way, the players would have a continually-changing, but logical framework, allowing them to progress with confidence; at first only obtaining orthogonally magic solutions, before becoming accomplished cubers and achieving diagonal magic success. Should a physical 3D deluxe version like this be impractical; an alternative virtual 3D deluxe magic box cube, that would include the lighting effects, could be created in downloadable apps, desktop applications, or in online simulators. An added advantage of a virtual cube would be that it could allow the choice of being able to automatically redress any numbers that would have become rotated in a physical version of the twisty puzzle.
Concerning the numbering system, we have already considered the choice of the net diagram in the order 4 example : The preferred net of the magic box cube is a priori a horizontal cross, which would allow for similarly-aligned numbers four faces horizontally, and three faces vertically (when counting the "front elevation," or intersection face, twice). A neat alternative would be a cube composed of two interlocking "U" strips of 3 faces; each strip with its own alignment of numbers. However, the preferred net diagram, with its unequal strips, might have the advantage of giving an extra clue to players for the correct orientation of the cubelets during reassembly; not forgetting of course that it should always be the numbers themselves, once understood and eventually memorised, that guide a player towards the solved state. Bearing in mind the importance of legibility, it may not be reasonable to exceed 3-digits. Condensed typeface styles can help meet the space constraints on the cubelets, but only up to a certain extent. With "normal" magic box cubes of even orders, an order n = 12, that already has 6n² - 12n + 8 = 728 cubelets, would, apart from probably being the maximum practical dimension, certainly be an enormous challenge!
Can the Magic Box Concept be Extended beyond Cubes to Other Magic Polyhedra?
Magic Box is a generic term, and apart from the cubic (or cuboid) puzzles, it could also refer to those that are based on other polyhedra. The Wikipedia page, "Combination puzzle," gives an idea of the multitude of different shapes and sizes of the diverse twisty puzzles which have been invented since the Rubik's Cube.
In 2006, Joshua Bell, a member of twisty.puzzles.com, compiled a fascinating page entitled "Magic Polyhedra* Patents," which lists of most of the major U.S. and European Patents relating to magic polyhedra, as issued between 1972 and 2001.
In 2012, Dénes Ferenc, another avid enthusiast, created an excellent Ruwix Twisty Puzzle Wiki. Its contents are encyclopaedic, and include almost everything you need to know about the Rubik's Cube™ and other polyhedral twisty puzzles.
Latest Developments
Inspired by the present article, Inder Taneja has published two papers entitled "Magic Cubes Based on Magic Squares" and "Universal and Upside-down Magic Cubes;" at first on his site, on the 9th and 10th October 2024; and then on Zenodo, on the 12th October 2024, before updating the latter with revised versions v2 on the 17th October 2024. Taneja proposes assemblies of special magic squares, such as bordered, striped, cornered, 180° rotatable, mirror looking, and upside-down versions, all in a Sudoko-Cube-like fashion.
Creative Commons
Except where otherwise noted, the ideas and contents of this article and its appendices, are licensed by the author, William Walkington, under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International licence. For details of the licence and instructions how to attribute this work, please refer to the CC BY-NC-SA 4.0 link in the adjoining sidebar. Other useful information (such as exceptions) can be found on the "Creative Commons" page, which is accessible via the header.



















