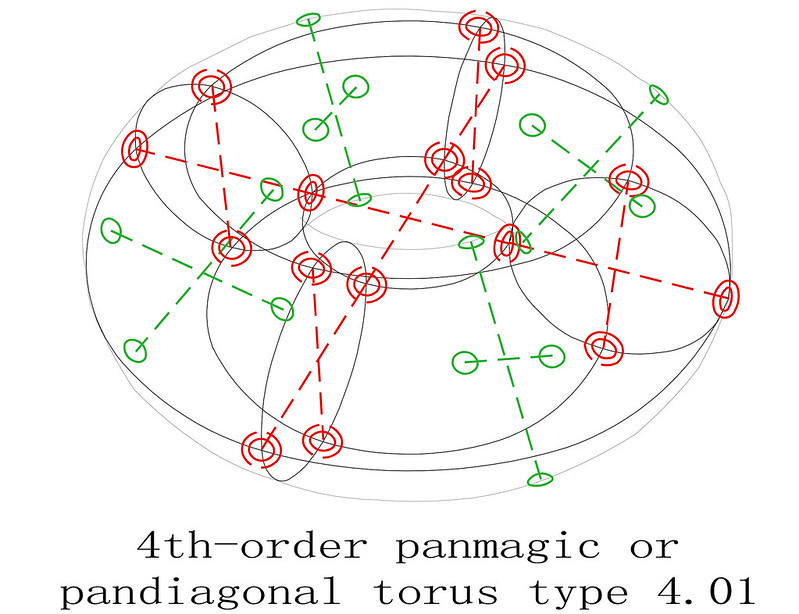
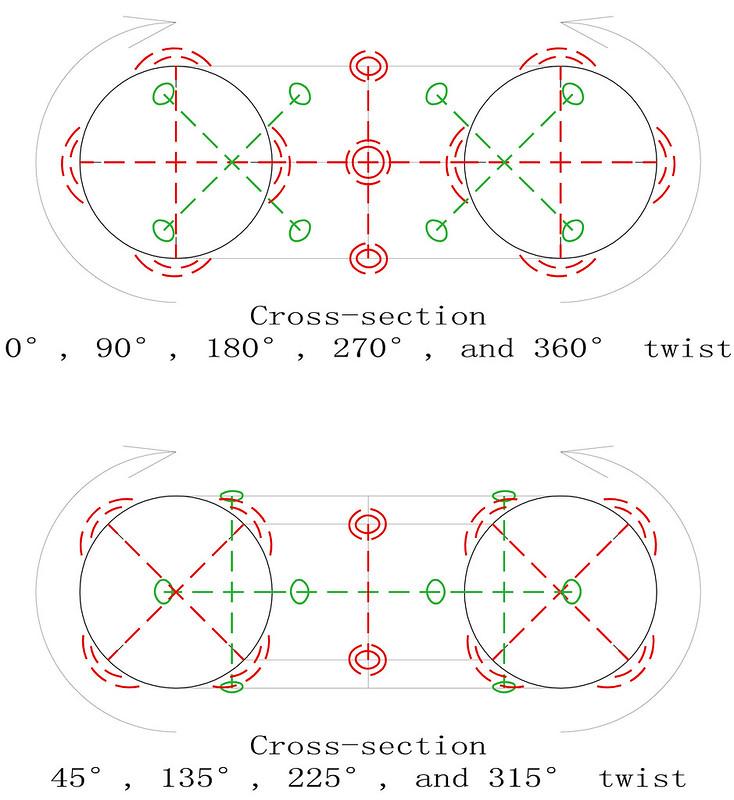
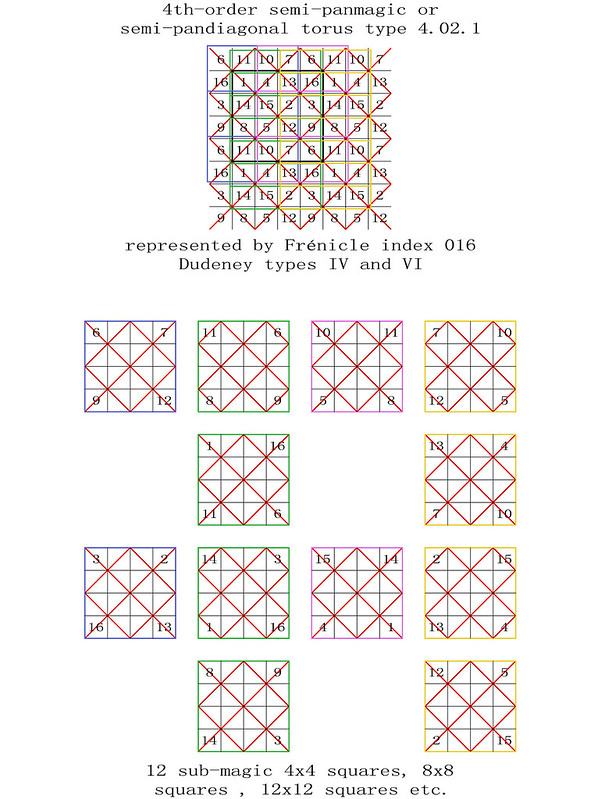
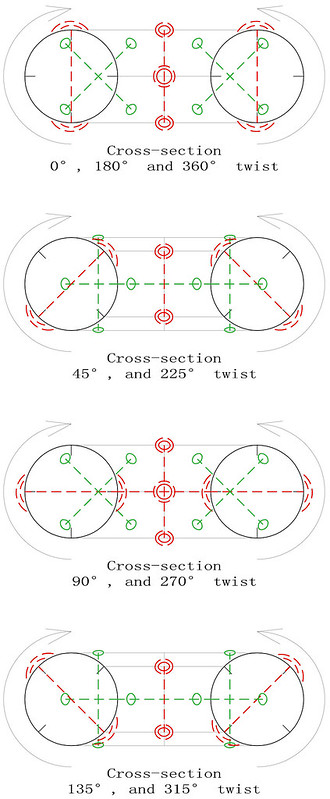
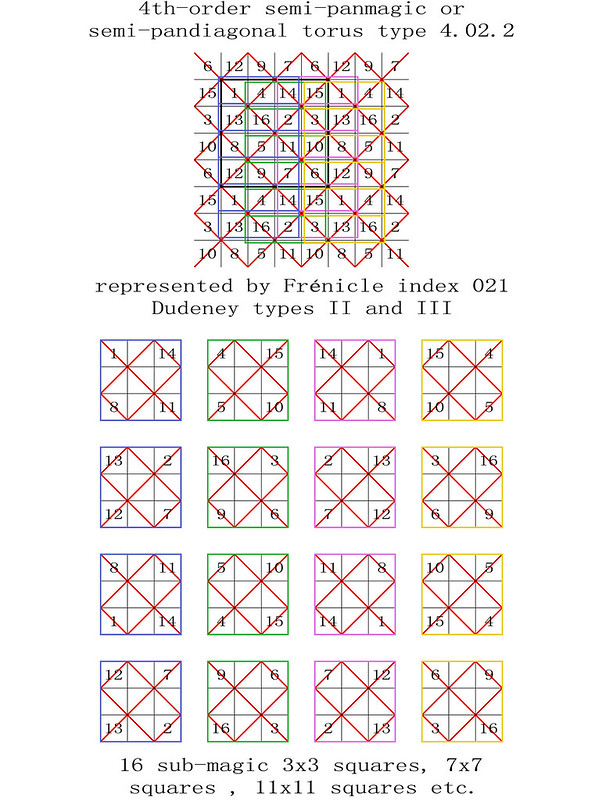
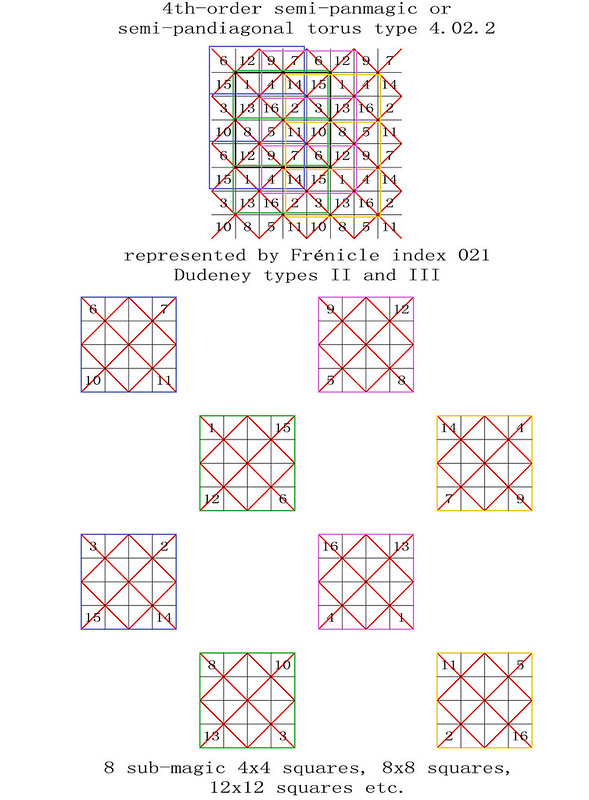
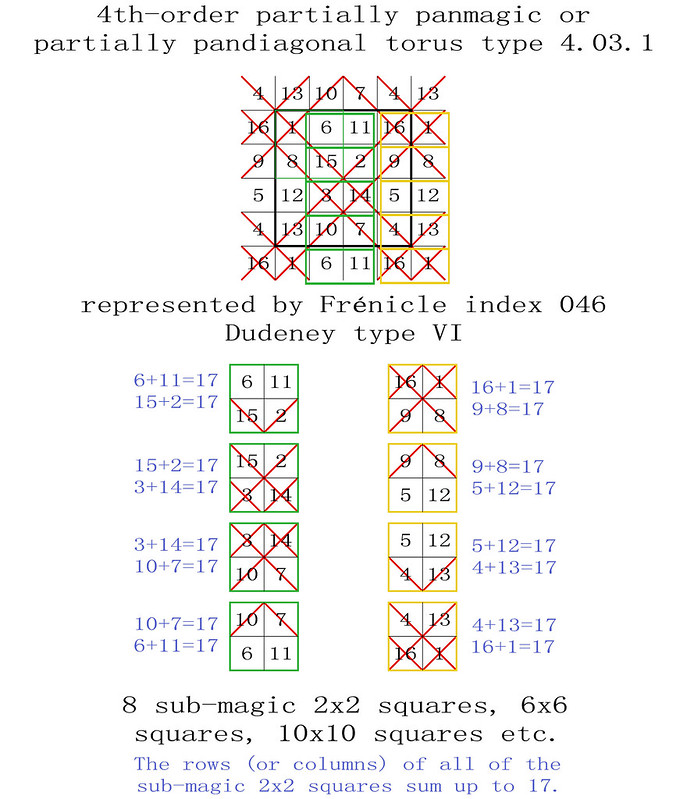
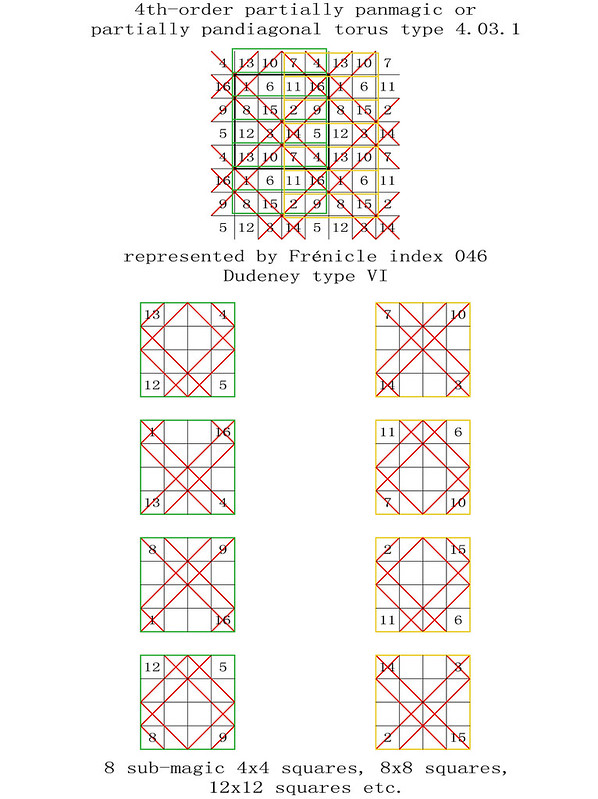
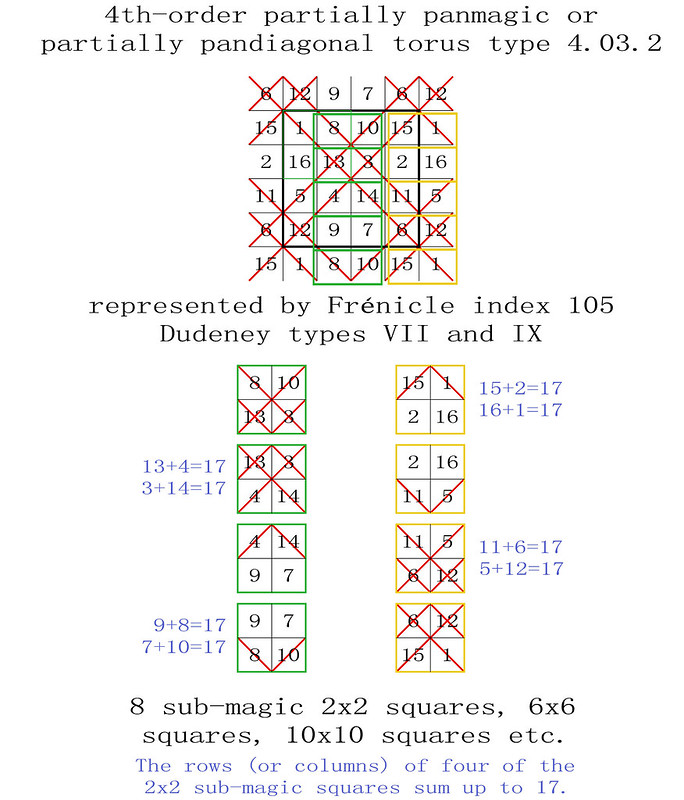
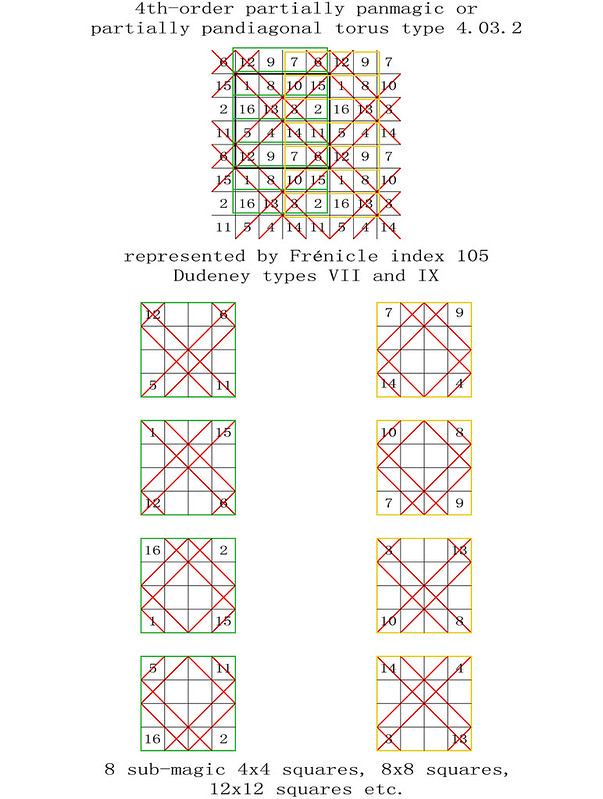
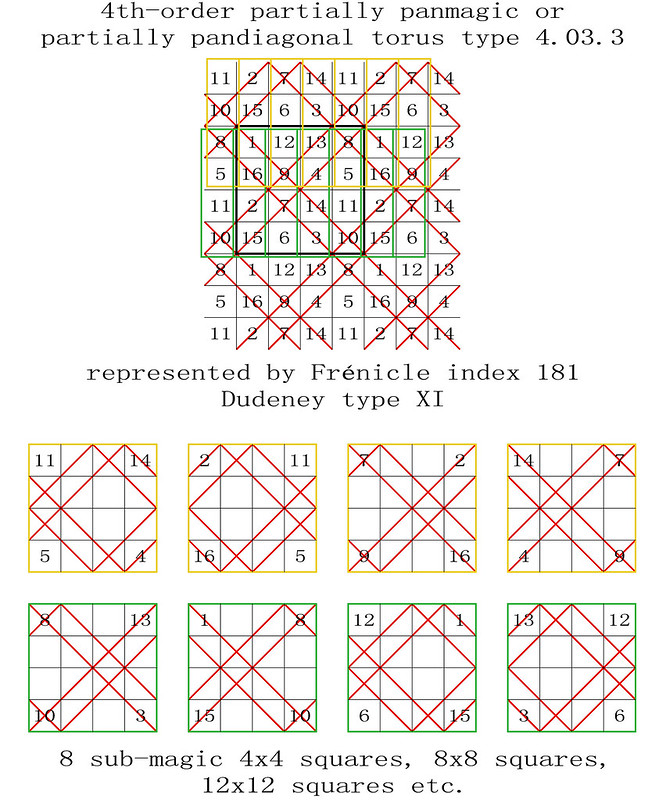
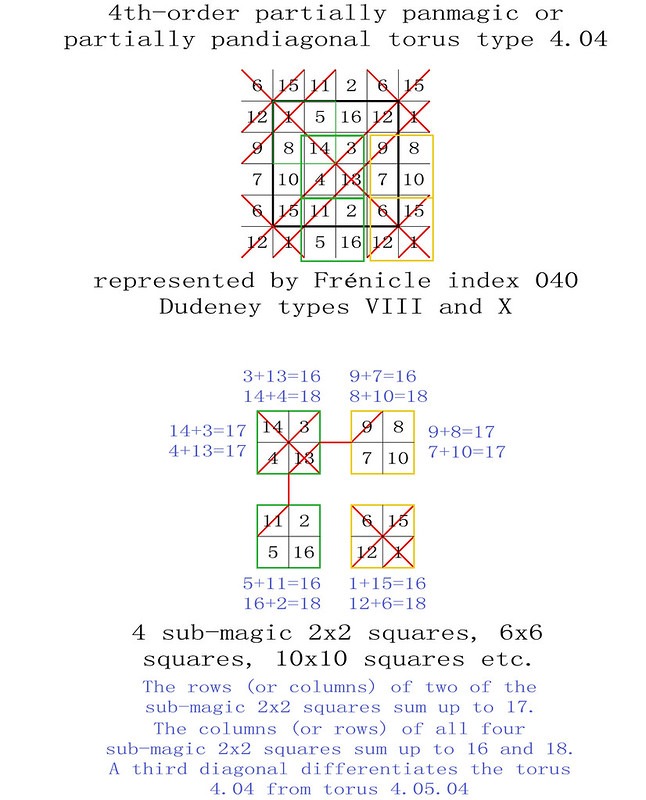
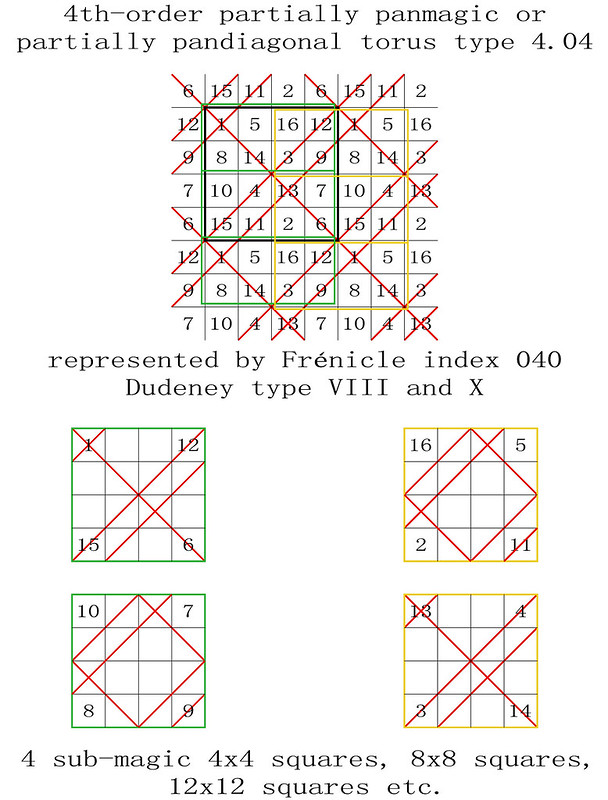
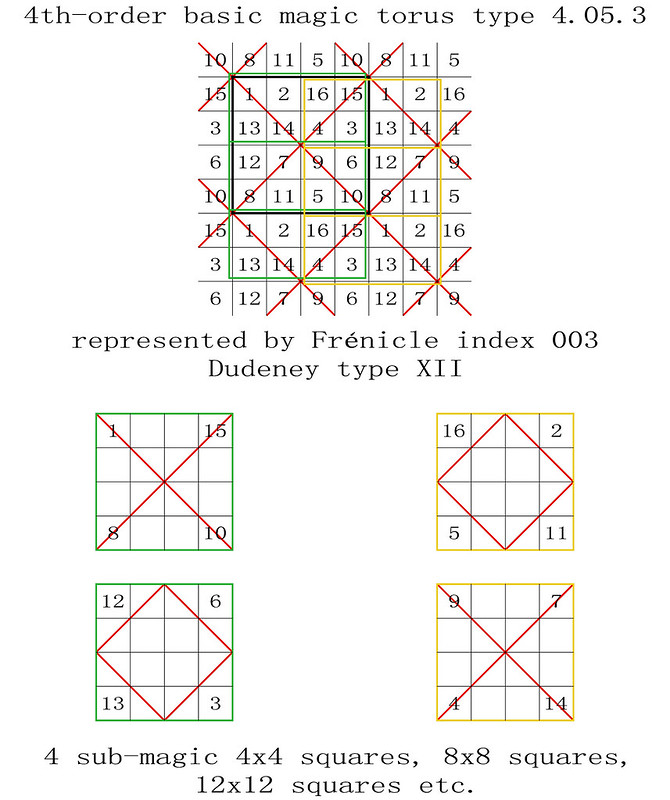
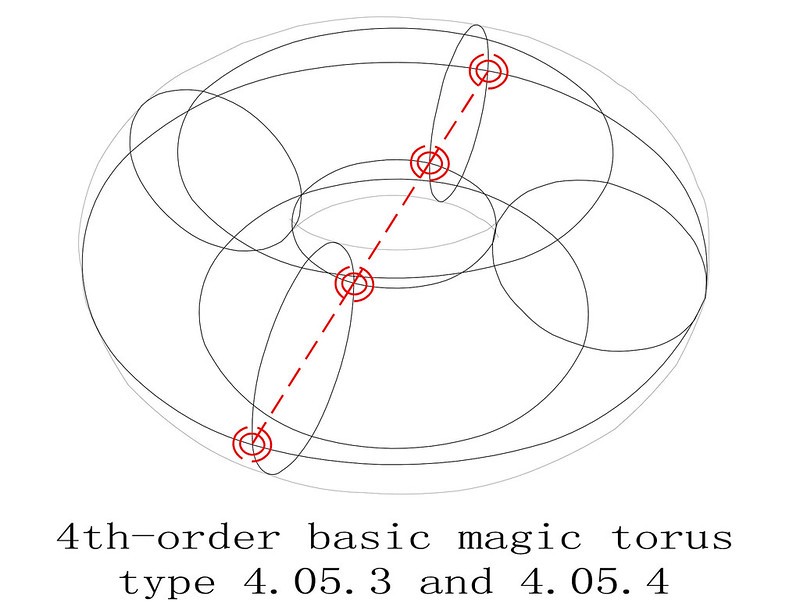
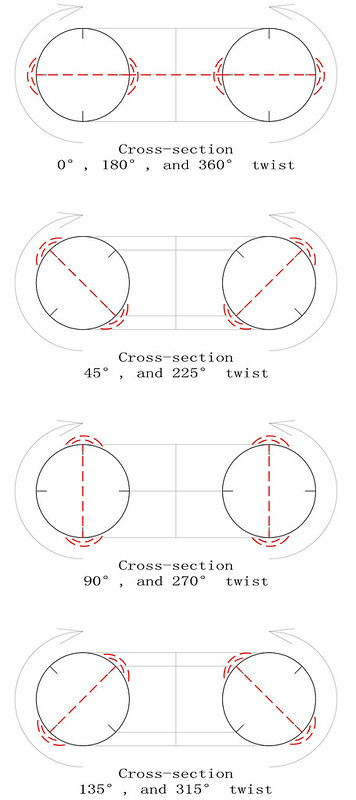
On the 8th April 2018, I was one of several magic square enthusiasts to receive a copy of a paper entitled "Magic Tetragonal Octahedron" that was sent to us by Miguel Angel Amela. Miguel is a prolific writer on recreational mathematics, and his papers are always a source of inspiration. This paper was no exception, as it prompted me to look into his subject, and make some humble contributions. What immediately interested me was that Magic Tetragonal Octahedra suggested possible links between numerical magic and geometry. Similar connections have already motivated my previous research in subjects that range from magic tori, to area magic squares and perimeter magic squares. The third dimension of Magic Tetragonal Octahedra offers new possibilities.
Magic Tetragonal Octahedra
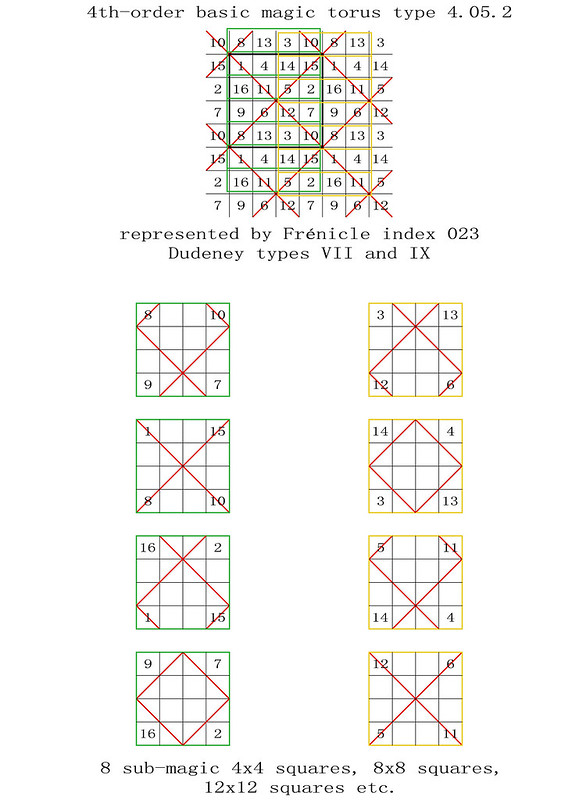
In his paper dated 8th April 2018, Miguel points out that many parallels can be drawn between normal magic squares and tetragonal octahedra. For example, in the octahedral family, the tetragonal types (known as tetragonal octahedra, or tetragonal trapezohedra, or tetragonal deltohedra) have 8 kite faces, 16 edges and 10 vertices. These totals can be compared with the 8 complementary pairs (for example 13 + 4 = n²+1), the 16 numbers (from 1 to 16), and the 10 magic line series (4 rows + 4 columns + 2 diagonals) that constitute a normal magic square of order-4. Miguel also observes that 8 faces + 16 edges + 10 vertices add up to 34, which is the magic constant of a normal magic square of order-4.
If the 16 edges of a tetragonal octahedron are numbered from 1 to 16, and if each of the 8 faces has 4 edge numbers that total 34, then we are looking at a Magic Tetragonal Octahedron. Miguel's first example is illustrated below:
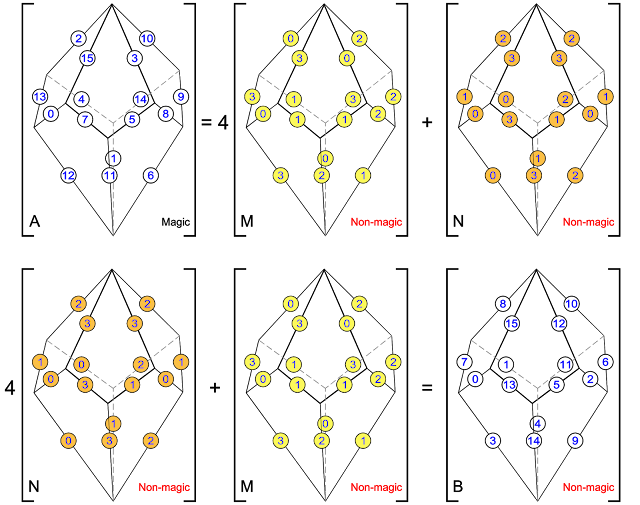
Miguel then checks if this Magic Tetragonal Octahedron is also purely magic. Purely magic is the term used by George Styan for magic squares where nM + N is magic, and M + nN is also magic, (when M and N are the basic matrices and n is the order of the square). For the first example of a Magic Tetragonal Octahedron (illustrated above), this is not the case, as shown by the factorization that follows:
Please note that for the factorization shown above, the natural numbers 1 to 16 are replaced by the numbers 0 to 15. Miguel points out that in this example, the basic octahedral matrices are non-magic, and that when the multiplier is interchanged, the result B is not a Magic Tetragonal Octahedron. The octahedral matrices are not mutually orthogonal.
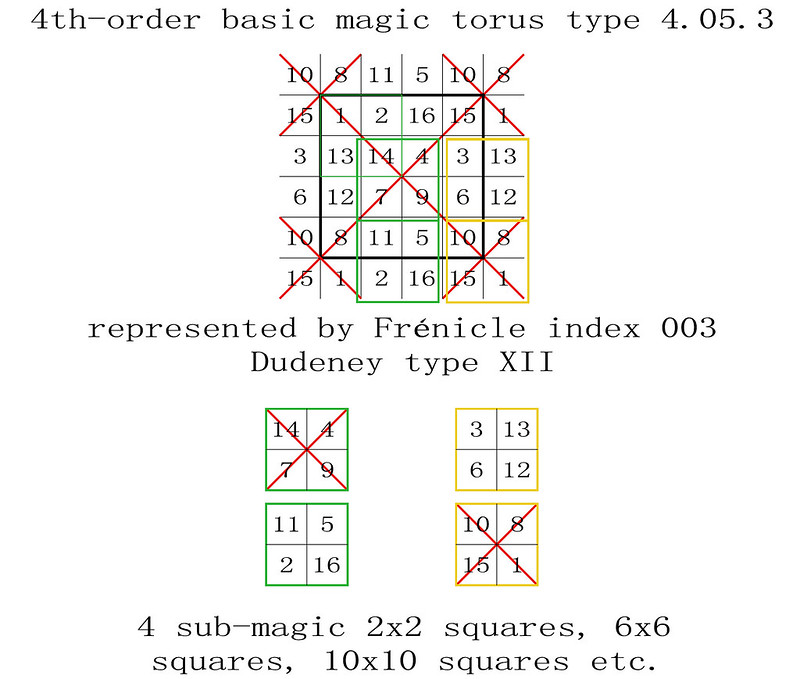
Miguel then shows the factorization of a Purely Magic Tetragonal Octahedron, as illustrated below:
In this second case, the basic octahedral matrices are magic, and when the multiplier is interchanged, the result D is also a Purely Magic Tetragonal Octahedron. The octahedral matrices are mutually orthogonal.
In his conclusion, Miguel Angel Amela indicates that using a Quick Basic program with 9 independent variables, and compiled with QB64, he has found that the total number of Magic Tetragonal Octahedron solutions is 1,792 (8 x 224), and that 128 (8 x 16) of these are Purely Magic.
Miguel states that his paper was inspired by a book that was sent to him by George Styan in 2012: This book by Fitting Friedrich is entitled “Panmagische Quadrate und Magische Sternvielecke.” The section that briefly describes Magic Tetragonal Octahedra is subtitled “Beziehung der magischen (8,2) - Sterne zu Körpern mit magischen Eigenschaften,” and can be found on the pages 62-63 of the 1939 edition of the Scientia Delectans, Germeinverständliche Darstellungen aus der Unterhaltungsmathematik und aux verwanden Gebieten, Heft 4.
Looking more closely at the examples given by Miguel Angel Amela I noticed something that had previously escaped my attention: I realised that 2 out of the 10 vertices of the Magic Tetragonal Octahedron were pole vertices where 4 edges met, whilst all of the other 8 vertices were the meeting points of only 3 edges. I therefore examined the pole vertices in more detail, using the same letters proposed by Miguel. For this study the polar vertices are therefore A and J:
For the first Magic Tetragonal Octahedron (figure A in the first factorization):
Pole vertex A: 2 + 10 + 3 + 15 = 30 (+ 4 for conversion) = 34 the magic constant for magic squares of order-4
Pole vertex J: 1 + 6 + 12 + 11 = 30 (+ 4 for conversion) = 34 the magic constant for magic squares of order-4
For the Purely Magic Tetragonal Octahedron (figure C in the second factorization):
Pole vertex A: 2 + 11 + 8 + 15 = 36 (+ 4 for conversion) = 40
Pole vertex J : 3 + 14 + 13 + 6 = 36 (+ 4 for conversion) = 40
For the Purely Magic Tetragonal Octahedron (figure D in the second factorisation):
Pole vertex A: 8 + 14 + 2 + 15 = 39 (+ 4 for conversion) = 43
Pole vertex J : 12 + 11 + 7 + 9 = 39 (+ 4 for conversion) = 43
On the 9th June 2018 I contacted Miguel to inform him about these observations, and to ask him, if he had the time, to use his programming skills to discover the answers to the following questions:
1/ Did the total of the edges that meet at pole A always equal the total of edges that meet at pole J?
2/ If so, what were the subtotals of the 1792 Magic Tetragonal Octahedra for each of the polar sums?
In the days that followed Miguel investigated further, and then wrote back to inform me that:
1/ For all 1792 solutions, the sum of the 4 edges of pole A = the sum of the 4 edges of pole J.
2/ For Magic Tetragonal Octahedra constructed using consecutive natural numbers from 1 to 16, the number of solutions is symmetric, with polar sums ranging from 19 to 49 (except for 20 or 48, which strangely do not exist), and the 288 solutions which have the polar sum of 34 (the magic constant of magic squares of order-4) are at the centre of this system. What is more, each of the solutions with polar sums of 34 has interesting equatorial symmetries:
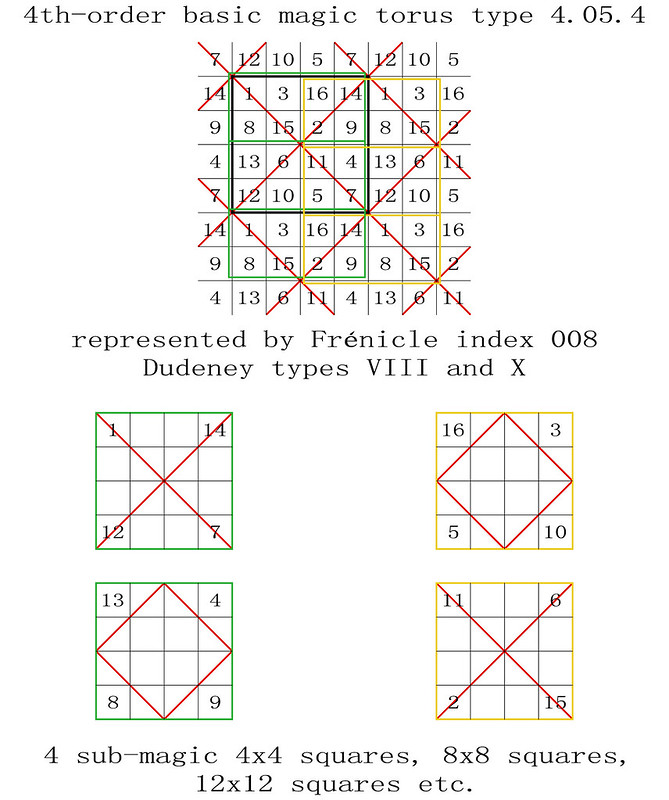
The 288 "most-magic" solutions with magic polar sums of 34 are particularly interesting, and Miguel and I have therefore decided to call these Panmagic Tetragonal Octahedra: Please refer to the very first figure of this post which, by a complete coincidence, turns out to be a good example!
On the 8th April 2018 I had another question for Miguel: "Is it possible to draw irregular Magic Tetragonal Octahedra using lines that have lengths in proportion to the numbers 1 to 16? And if this is possible, and the faces are still planar, what are the implications for the areas of the faces?"
For the time being, at the date of posting this article, this question remains unanswered. I have attempted to construct a virtual model using Sketchup and Autocad, but the exercise is too difficult without precise coordinates for the vertices. I have also tried to physically construct a scale model, but was faced with a practical problem: As the octahedron kite edges lack structural triangulation, the resulting instability is an impediment to making accurate measurements... Apparently the solution will have to come from an algorithm that will produce precise coordinates of the vertices, depending on the relative positions of the edges 1 to 16. And once this is achieved, we should be able to construct the irregular polyhedron and answer the following questions:
Are the 8 kite faces continuous or folded planar surfaces?
Do the kite areas have special characteristics?
Does the volume of the irregular Magic Tetragonal Octahedron have special characteristics?
Should a reader wish to contribute, please send me the precise x, y and z coordinates of the vertices that define an irregular Panmagic Tetragonal Octahedron. No prizes can be given, but the authors of pertinent solutions will, if they agree, have their findings published here.
I wish to thank Miguel Angel Amela for bringing this interesting aspect of magic geometry to my attention, and for authorising me to publish the contents of his paper.
 |
| Magic Tetragonal Octahedron by Miguel Angel Amela - Graphics by William Walkington |
Miguel then checks if this Magic Tetragonal Octahedron is also purely magic. Purely magic is the term used by George Styan for magic squares where nM + N is magic, and M + nN is also magic, (when M and N are the basic matrices and n is the order of the square). For the first example of a Magic Tetragonal Octahedron (illustrated above), this is not the case, as shown by the factorization that follows:
 |
| Magic Tetragonal Octahedron Factorization by Miguel Angel Amela - Graphics by William Walkington |
Miguel then shows the factorization of a Purely Magic Tetragonal Octahedron, as illustrated below:
 |
| Purely Magic Tetragonal Octahedron Factorization by Miguel Angel Amela - Graphics by William Walkington |
In his conclusion, Miguel Angel Amela indicates that using a Quick Basic program with 9 independent variables, and compiled with QB64, he has found that the total number of Magic Tetragonal Octahedron solutions is 1,792 (8 x 224), and that 128 (8 x 16) of these are Purely Magic.
Miguel states that his paper was inspired by a book that was sent to him by George Styan in 2012: This book by Fitting Friedrich is entitled “Panmagische Quadrate und Magische Sternvielecke.” The section that briefly describes Magic Tetragonal Octahedra is subtitled “Beziehung der magischen (8,2) - Sterne zu Körpern mit magischen Eigenschaften,” and can be found on the pages 62-63 of the 1939 edition of the Scientia Delectans, Germeinverständliche Darstellungen aus der Unterhaltungsmathematik und aux verwanden Gebieten, Heft 4.
Observations and Further Developments
Looking more closely at the examples given by Miguel Angel Amela I noticed something that had previously escaped my attention: I realised that 2 out of the 10 vertices of the Magic Tetragonal Octahedron were pole vertices where 4 edges met, whilst all of the other 8 vertices were the meeting points of only 3 edges. I therefore examined the pole vertices in more detail, using the same letters proposed by Miguel. For this study the polar vertices are therefore A and J:
For the first Magic Tetragonal Octahedron (figure A in the first factorization):
Pole vertex A: 2 + 10 + 3 + 15 = 30 (+ 4 for conversion) = 34 the magic constant for magic squares of order-4
Pole vertex J: 1 + 6 + 12 + 11 = 30 (+ 4 for conversion) = 34 the magic constant for magic squares of order-4
For the Purely Magic Tetragonal Octahedron (figure C in the second factorization):
Pole vertex A: 2 + 11 + 8 + 15 = 36 (+ 4 for conversion) = 40
Pole vertex J : 3 + 14 + 13 + 6 = 36 (+ 4 for conversion) = 40
For the Purely Magic Tetragonal Octahedron (figure D in the second factorisation):
Pole vertex A: 8 + 14 + 2 + 15 = 39 (+ 4 for conversion) = 43
Pole vertex J : 12 + 11 + 7 + 9 = 39 (+ 4 for conversion) = 43
On the 9th June 2018 I contacted Miguel to inform him about these observations, and to ask him, if he had the time, to use his programming skills to discover the answers to the following questions:
1/ Did the total of the edges that meet at pole A always equal the total of edges that meet at pole J?
2/ If so, what were the subtotals of the 1792 Magic Tetragonal Octahedra for each of the polar sums?
In the days that followed Miguel investigated further, and then wrote back to inform me that:
1/ For all 1792 solutions, the sum of the 4 edges of pole A = the sum of the 4 edges of pole J.
2/ For Magic Tetragonal Octahedra constructed using consecutive natural numbers from 1 to 16, the number of solutions is symmetric, with polar sums ranging from 19 to 49 (except for 20 or 48, which strangely do not exist), and the 288 solutions which have the polar sum of 34 (the magic constant of magic squares of order-4) are at the centre of this system. What is more, each of the solutions with polar sums of 34 has interesting equatorial symmetries:
 |
| Table of the polar sums of Magic Tetragonal Octahedra by Miguel Angel Amela - Graphics by William Walkington |
The 288 "most-magic" solutions with magic polar sums of 34 are particularly interesting, and Miguel and I have therefore decided to call these Panmagic Tetragonal Octahedra: Please refer to the very first figure of this post which, by a complete coincidence, turns out to be a good example!
What are the Possible Implications of an Irregular Magic Tetragonal Octahedron?
On the 8th April 2018 I had another question for Miguel: "Is it possible to draw irregular Magic Tetragonal Octahedra using lines that have lengths in proportion to the numbers 1 to 16? And if this is possible, and the faces are still planar, what are the implications for the areas of the faces?"
For the time being, at the date of posting this article, this question remains unanswered. I have attempted to construct a virtual model using Sketchup and Autocad, but the exercise is too difficult without precise coordinates for the vertices. I have also tried to physically construct a scale model, but was faced with a practical problem: As the octahedron kite edges lack structural triangulation, the resulting instability is an impediment to making accurate measurements... Apparently the solution will have to come from an algorithm that will produce precise coordinates of the vertices, depending on the relative positions of the edges 1 to 16. And once this is achieved, we should be able to construct the irregular polyhedron and answer the following questions:
Are the 8 kite faces continuous or folded planar surfaces?
Do the kite areas have special characteristics?
Does the volume of the irregular Magic Tetragonal Octahedron have special characteristics?
Should a reader wish to contribute, please send me the precise x, y and z coordinates of the vertices that define an irregular Panmagic Tetragonal Octahedron. No prizes can be given, but the authors of pertinent solutions will, if they agree, have their findings published here.
Acknowledgement
I wish to thank Miguel Angel Amela for bringing this interesting aspect of magic geometry to my attention, and for authorising me to publish the contents of his paper.