In traditional magic squares the sums of each row and column are equal, and in traditional pandiagonal (or in traditional panmagic) squares the sums are also equal along the different diagonals. Why not look into diagonal magic squares where all the different diagonals are magic and the rows and columns play the role of diagonals in traditional magic squares? This concept might seem quite simple, as with a 45° rotation of an odd-order magic square a diagonally magic square will be produced. However, things get more complicated with even-order squares, and at my request, Walter Trump kindly programmed his computer to determine the different types and quantities of diagonally magic 4th order tori. The results are illustrated below:
Fourth-Order Diagonal Magic Tori
DT 4.01 Diagonal Panmagic Tori Type 1
with 8 crossed horizontal and vertical magic lines producing 16 magic intersections
This diagonal torus type DT4.01 is the same traditional pandiagonal torus type T4.01 that has already been identified in a previous article! This panmagic torus type is an important link between the traditional magic system and the diagonally magic system that we are now exploring.
Total : 3 diagonal panmagic tori type 1 that display 48 diagonal panmagic squares
DT 4.02 Diagonal Partially Panmagic Tori Type 2
with 4 x 2 crossed horizontal and vertical magic lines producing 8 magic intersections
with 4 x 2 crossed horizontal and vertical magic lines producing 8 magic intersections
Total : 29 diagonal partially panmagic tori type 2 that display 464 diagonal partially panmagic squares
DT 4.03 Diagonal Partially Panmagic Tori Type 3
with 2 x 2 crossed horizontal and vertical magic lines producing 4 magic intersections
with 2 x 2 crossed horizontal and vertical magic lines producing 4 magic intersections
Total : 698 diagonal partially panmagic tori type 3 that display 11,168 diagonal partially panmagic squares
DT 4.04 Diagonal Partially Panmagic Tori Type 4
with 4 x 1 crossed horizontal and vertical magic lines producing 4 magic intersections
with 4 x 1 crossed horizontal and vertical magic lines producing 4 magic intersections
Total : 6 diagonal partially panmagic tori type 4 that display 96 diagonal partially panmagic squares
DT 4.05 Diagonal Partially Panmagic Tori Type 5
with 2 x 1 crossed horizontal and vertical magic lines producing 2 magic intersections
with 2 x 1 crossed horizontal and vertical magic lines producing 2 magic intersections
Total : 332 diagonal partially panmagic tori type 5 that display 5,312 diagonal partially panmagic squares
DT 4.06 Diagonal Magic Tori Type 6
with a pair of crossed horizontal and vertical magic lines producing 1 magic intersection
with a pair of crossed horizontal and vertical magic lines producing 1 magic intersection
Total : 1,968 diagonal magic tori type 6 that display 31,488 diagonal magic squares
GRAND TOTAL OF THE DIAGONAL MAGIC TORI :
3,036 FOURTH-ORDER DIAGONAL MAGIC TORI
THAT DISPLAY 48,576 DIAGONAL MAGIC SQUARES
Observations
1/ Please note that as the three diagonal panmagic tori type DT4.01 are completely magic, they also belong to the traditional magic system, and have already been counted as pandiagonal type T4.01 in the total of the fourth-order magic tori.
2/ Unlike the 4x4 traditional magic squares, which have magic diagonals that cross at their centre, even-order diagonal magic squares cannot have centrally intersecting horizontal and vertical magic lines. This is why I have decided to describe all squares on a same torus as having the same magic value as the torus itself. A torus is more or less magic depending on the number of magic intersections that occur on its surface and the same should apply to all the squares that it displays.
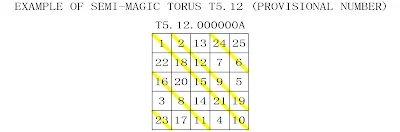
3/ Semi-magic diagonal tori are considered to have all diagonals magic, but no magic intersection of horizontal and vertical magic lines occurs on their surface. The examples of semi-magic diagonal tori found by Walter Trump's computer calculations are as follows:
Fourth-Order Diagonal Semi-Magic Tori
DT 4.07 Diagonal Semi-Magic Tori Type 7
with 4 parallel horizontal or vertical magic lines producing no magic intersections
with 4 parallel horizontal or vertical magic lines producing no magic intersections
Total : 631 diagonal semi-magic tori type 7 that display 10,096 diagonal semi-magic squares
DT 4.08 Diagonal Semi-Magic Tori Type 8
with 2 parallel horizontal or vertical magic lines producing no magic intersections
with 2 parallel horizontal or vertical magic lines producing no magic intersections
Total : 18,895 diagonal semi-magic tori type 8 that display 302,320 diagonal semi-magic squares
DT 4.09 Diagonal Semi-Magic Tori Type 9
with 1 horizontal or vertical magic line producing no magic intersection
with 1 horizontal or vertical magic line producing no magic intersection
Total : 28,214 diagonal semi-magic tori type 9 that display 451,424 diagonal semi-magic squares
DT 4.10 Diagonal Semi-Magic Tori Type 10
with no horizontal or vertical magic lines
Total : 165,800 diagonal semi-magic tori type 10 that display 2,652,800 diagonal semi-magic squares
GRAND TOTAL OF THE DIAGONAL SEMI-MAGIC TORI :
213,540 FOURTH-ORDER DIAGONAL SEMI-MAGIC TORI
THAT DISPLAY 3,416,640 DIAGONAL SEMI-MAGIC SQUARES
Walter Trump points out the special properties of many of the above diagonal magic or semi-magic tori where the sum of the two numbers at opposite corners of any displayed 3x3 subsquare is N²+1 = 17. Examples of such diagonal magic tori are illustrated below:
Fourth-Order Special Diagonal Magic Tori and Special Diagonal Semi-Magic Tori
Special DT 4.01 Diagonal Panmagic Tori Type 1
with 8 crossed horizontal and vertical magic lines producing 16 magic intersections
This diagonal torus type DT4.01 is the same traditional pandiagonal torus type T4.01 that has already been identified in a previous article! This panmagic torus type is an important link between the traditional magic system and the diagonally magic system that we are now exploring.
Total : 3 special diagonal panmagic tori type 1 that display 48 diagonal panmagic squares
Special DT 4.02 Diagonal Partially Panmagic Tori Type 2
with 4x2 crossed horizontal and vertical magic lines producing 8 magic intersections
Special DT 4.03 Diagonal Partially Panmagic Tori Type 3
with 2x2 crossed horizontal and vertical magic lines producing 4 magic intersections
with 2x2 crossed horizontal and vertical magic lines producing 4 magic intersections
Total : 656 special diagonal partially panmagic tori type 3 that display 10,496 special diagonal partially panmagic squares
Special DT 4.07 Diagonal Semi-Magic Tori Type 7
with 4 parallel horizontal or vertical magic lines producing no magic intersections
with 4 parallel horizontal or vertical magic lines producing no magic intersections
Total : 400 special diagonal semi-magic tori type 7 that display 6,400 special diagonal semi-magic squares
Special DT 4.08 Diagonal Semi-Magic Tori Type 8
with 2 parallel horizontal or vertical magic lines producing no magic intersections
with 2 parallel horizontal or vertical magic lines producing no magic intersections
Total : 14,502 special diagonal semi-magic tori type 8 that display 232,032 special diagonal semi-magic squares
Special DT 4.10 Diagonal Semi-Magic Tori Type 10
with no horizontal or vertical magic lines
Total : 65,053 special diagonal semi-magic tori type 10 that display 1,040,848 special diagonal semi-magic squares
GRAND TOTAL OF THE SPECIAL DIAGONAL MAGIC TORI AND SPECIAL DIAGONAL SEMI-MAGIC TORI :
80,640
The total number of special diagonal tori (magic and semi-magic) is 80,640 (if we include the 3 pandiagonal tori that are already counted as pandiagonal type T4.01 in the total of the fourth-order magic tori).
Walter Trump points out that :N(4) = 8! x 2
N(4) = (8 x 7 x 6 x 5 x 4 x 3 x 2 x 1) x 2
N(4) = 80 640