Multiplicative Magic Tori

Because the present-day definition of complementary and self-complementary magic squares can be over-restrictive when studying magic tori, an alternative modular arithmetic interpretation is therefore proposed.

This approach suggests a new direction for research on magic squares (or magic tori), using modular multiplication, modular addition, and modular exponentiation.

Multiplicative Magic Tori (MMT) are examined throughout the orders 1 to 4. (Although there is no magic torus of order-2, there is a Multiplicative Diagonally Semi-Magic Torus (MDSMT)). The study then continues with a partial inspection of various examples from higher-orders, including some bimagic MMT of order-8.

A typical Multiplicative Magic Torus (MMT), or Multiplicative Magic Square (MMS) of order-4

The results include a new census of the Multiplicative Magic Tori (MMT) and Multiplicative Magic Squares (MMS) of orders 1 to 4. A detailed classification of the 82 Multiplicative Magic Tori (MMT) and 220 Multiplicative Magic Squares (MMS) of order-4 is given, together with explanatory graphics that highlight the main relationships and links.

In addition, it is shown that the diagonally magic, diagonally semi-magic, and lesser-magic tori, which are also present on the MMT, have special orthogonal sums. Some other interesting characteristics of modular exponentiations are also examined and commented.

The conclusions are presented in the form of integer sequences. Any input that might confirm, correct, or usefully append these findings, would be much appreciated

New Developments! 

Posted on the 24th April 2024, a new article entitled "Plus or Minus Groups of Magic Tori of Order 4" now demonstrates that the 255 magic tori of order 4 come from 137 ± Groups!

Although "Plus or Minus Groups of Magic Tori of Order 4" proposes an alternative way of looking at things, the "Multiplicative Magic Tori" represents valid intermediary research, and therefore remains available below.

Multiplicative Magic Tori (outdated by findings in the 137 ± Groups)

Please note that if you click on the button that appears at the top right hand side of the pdf viewer below, a new window will open and full size pages of "Multiplicative Magic Tori" will then be displayed, with options for zooming.

Read more ...

Magic Torus Coordinate and Vector Symmetries

Magic squares have fascinated mathematicians for centuries and they continue to do so today. However, many questions remain unanswered, and this study proposes a different perspective in order to shed new light on what magic squares are and how they work. Considering magic squares to be flattened partial viewpoints of convex or concave magic tori, the implied Gaussian surfaces require a modular arithmetic approach that is tested and analysed here.

Until today, most magic square construction methods use base squares, whilst "Magic Torus Coordinate and Vector Symmetries" proposes modular coordinate equations that not only define specific magic tori, but also generate their magic torus descendants.

The construction of Agrippa's traditional magic squares is analysed in detail for each of the seven planetary magic tori, and modular coordinate equations are defined that generate descendant tori throughout the respective higher-orders, whether they be odd, doubly-even, or singly-even.

The unique third-order magic torus and also a fifth-order pandiagonal torus of Latin construction are examined in detail. The modular coordinate equations that are defined generate an interesting variety of higher-odd-order descendant tori.

The study also explores the construction of the 12 different types of fourth-order magic tori, as well as the generation of their doubly-even magic torus descendants. In addition, a fourth-order Candy-style perfect square pandiagonal torus, and a fourth-order unidirectionally pandiagonal semi-magic torus, are each analysed in detail, and their torus descendants generated, throughout their respective higher-orders.

At the end of the study observations are made, and some conclusions are drawn as to the signification of the findings, and the potential for future research.

Some sample illustrations of a fourth-order partially pandiagonal torus and its partially pandiagonal torus descendants are shown below:

T4.195 4th-order partially pandiagonal torus

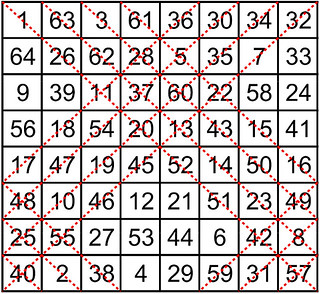8th-order partially pandiagonal torus, direct descendant of T4.195

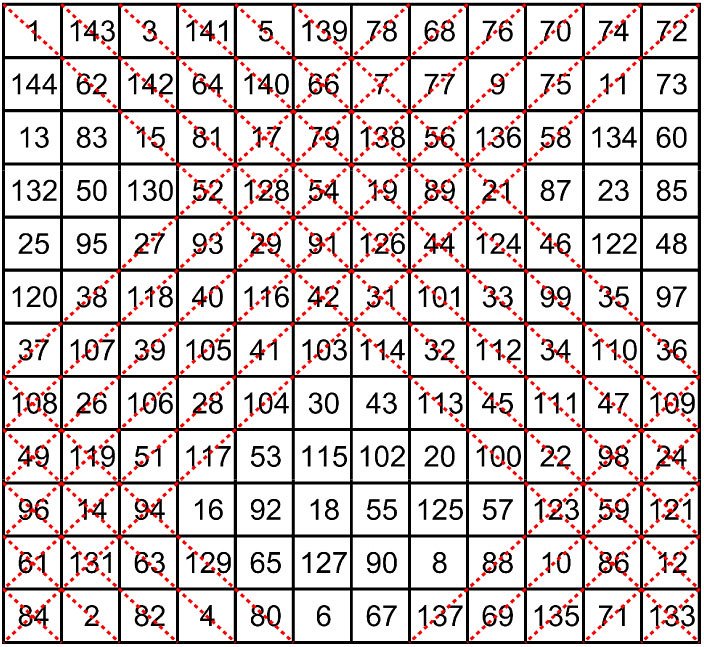12th-order partially pandiagonal torus, direct descendant of T4.195

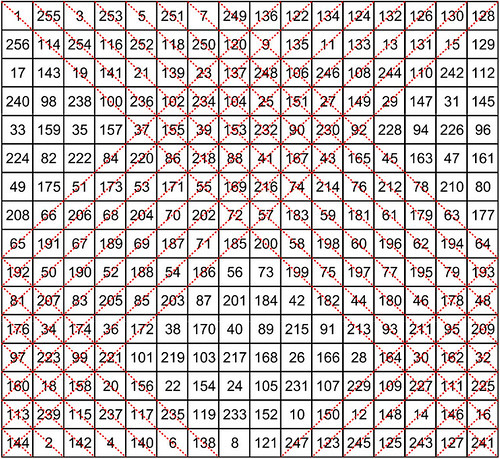16th-order partially pandiagonal torus, direct descendant of T4.195

To download "Magic Torus Coordinate and Vector Symmetries" from Google Drive, please use the following link: MTCVS 161019. The 134 Mo pdf file exceeds the maximum size (25 Mo) that Google Drive can scan, but as the file is virus free you can download it safely. Depending on the speed of your computer, the download can take up to two or three minutes to complete.

Read more ...