A partially pandiagonal order-9 magic square has recently been brought to my attention by Professor Peter D. Loly, a Senior Scholar at the University of Manitoba.
This order-9 square, initially published by the late Dame Kathleen Ollerenshaw in her article "Constructing pandiagonal magic squares of arbitrarily large size" (Mathematics Today, February 2006), was later analysed in 2013 by Ian Cameron, Adam Rogers and Peter D. Loly, in their paper "Signatura of Magic and Latin Integer Squares: Isentropic Clans and Indexing."
Cameron, Rogers and Loly have attributed the reference number dko9a to the square, and have described its characteristics in their table 4. In a recent correspondence, Peter D. Loly has pointed out that the square has a rank 5 matrix, which is the lowest he has seen for the order-9.
The dko9a is a single square viewpoint of a partially pandiagonal torus, which in this case displays a total of 26 other essentially different partially pandiagonal squares, plus 54 essentially different semi-magic (although still partially pandiagonal) squares. It is practical to consider the dko9a square as a torus, in order to define its construction by a formula, and thus generate its torus ascendants and descendants throughout its respective lower and higher-orders. To find out more about the approach and the method, please refer to "Magic Torus Coordinate and Vector Symmetries."
After observing the symmetries of the ninth-order partially pandiagonal square dko9a, we can deduce that if N is the order of the magic torus that displays this square, and if B represents any of the numbers of the torus from 1 to N², then the modular coordinates of the position vectors from the number 1 to any of the numbers B can be expressed as follows:
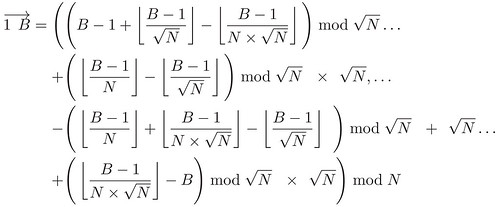 |
| Formula for the position vectors of the numbers of the magic torus that displays the dko9a square |
The second equation that follows is a simplified version in which B represents any of the numbers of the torus from 0 to N²-1, and the modular coordinates of the position vectors are specified from the origin number 0 to any of the numbers B. (Then, by adding 1 to all of the numbers 0 to N²-1 once they are positioned, we obtain the same result as in the first equation) :
 |
| Formula for the position vectors of the numbers 0 to N²-1 of the magic torus that displays the dko9a square -1 |
Generated by either of these methods, the following figures show partially pandiagonal tori of direct lineage in the first, fourth, ninth, sixteenth and twenty-fifth perfect-square-orders:
| First-order (1+1)/2 pandiagonal torus T1, ascendant of T4.173 |
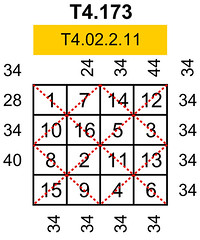 |
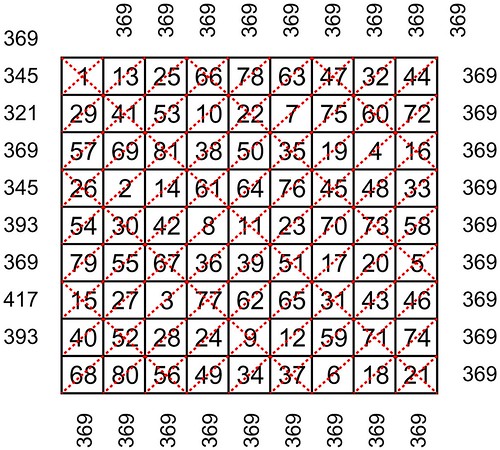
| Fourth-order (2+2)/8 pandiagonal (semi-pandiagonal) torus T4.173 |
 |
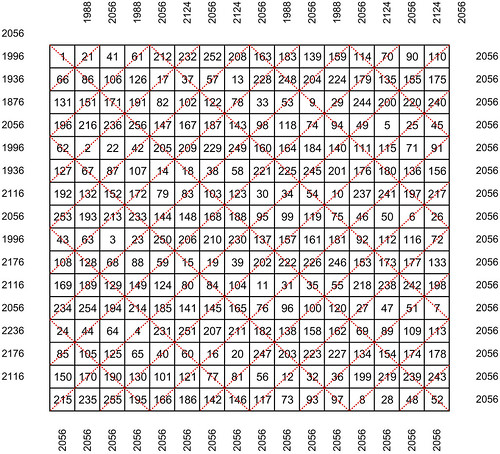
| Ninth-order (3+9)/18 pandiagonal torus, descendant of T4.173 (seen from Ollerenshaw's dko9a magic square viewpoint) |
 |
| Sixteenth-order (4+8)/32 pandiagonal torus, descendant of T4.173 |
 |
| Twenty-fifth-order (5+25)/50 pandiagonal torus, descendant of T4.173 |
Apart from the first-order torus T1, the immediate torus ascendant of the dko9a is the fourth-order semi-pandiagonal torus with index number T4.173 and type number T4.02.2.11. This torus displays eight semi-pandiagonal squares with Frénicle index numbers 89, 183, 323, 368, 464, 539, 661, and 698. The T4.173 torus also displays eight semi-magic squares and is entirely covered by 8 sub-magic 2x2 squares. For details of the classification of the 255 fourth-order magic tori by type numbers, please refer to "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus." For details of the classification of the 255 fourth-order magic tori by index numbers, (which, by using normalised squares is in a way a homage to Bernard Frénicle de Bessy), please refer to the "Table of Fourth-Order Magic Tori."
Please note that other formulae may well generate different torus ascendants or descendants. However, the formulae shown above are ideal, as they theoretically generate an infinite number of similarly constructed partially pandiagonal torus descendants throughout the higher-perfect-square-orders.
Observing the partially pandiagonal characteristics of these perfect-square-order magic tori suggests that there are recurring patterns:
In the odd-orders, the patterns of the magic diagonals are (1+1)/2 for the first-order, (3+9)/18 for the ninth-order, and (5+25)/50 for the twenty-fifth-order. This suggests a possible recurring pattern of (√N+N)/2N for the magic diagonals of the odd-orders that are generated by the perfect-square-order formulae described above.
In the even-orders, the patterns of the magic diagonals are (2+2)/2 for the fourth-order, and (4+8)/32 for the sixteenth-order. This suggests a possible recurring pattern of (√N+N/2)/2N for the magic diagonals of the even-orders that are generated by the perfect-square-order formulae described above.
Testing in higher-orders, or a mathematical proof, will validate or invalidate these hypotheses.
In the odd-orders, the patterns of the magic diagonals are (1+1)/2 for the first-order, (3+9)/18 for the ninth-order, and (5+25)/50 for the twenty-fifth-order. This suggests a possible recurring pattern of (√N+N)/2N for the magic diagonals of the odd-orders that are generated by the perfect-square-order formulae described above.
In the even-orders, the patterns of the magic diagonals are (2+2)/2 for the fourth-order, and (4+8)/32 for the sixteenth-order. This suggests a possible recurring pattern of (√N+N/2)/2N for the magic diagonals of the even-orders that are generated by the perfect-square-order formulae described above.
Testing in higher-orders, or a mathematical proof, will validate or invalidate these hypotheses.


