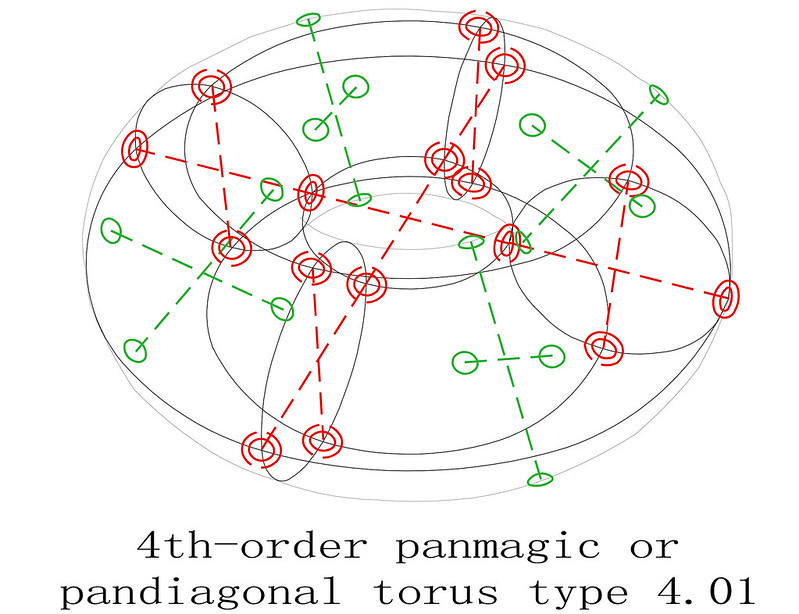
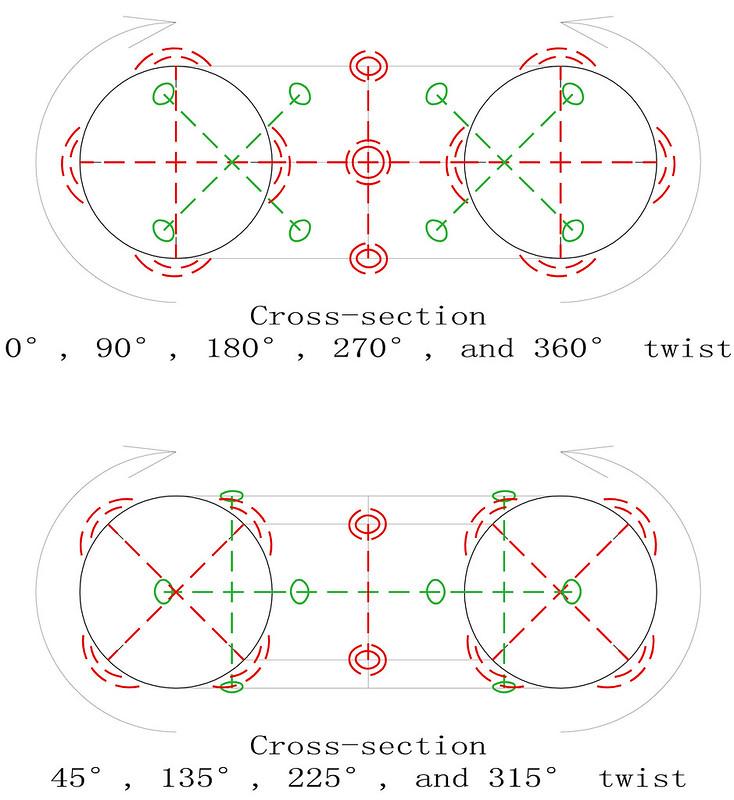
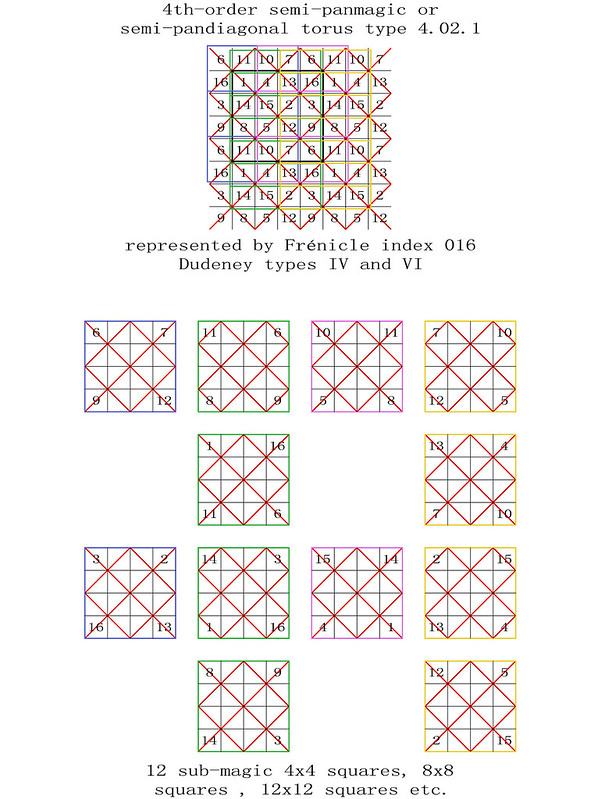
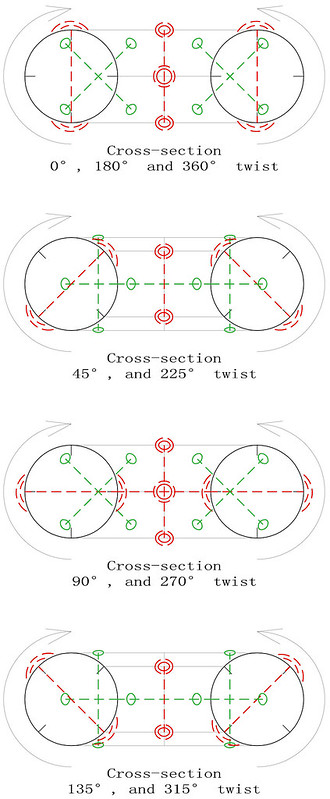
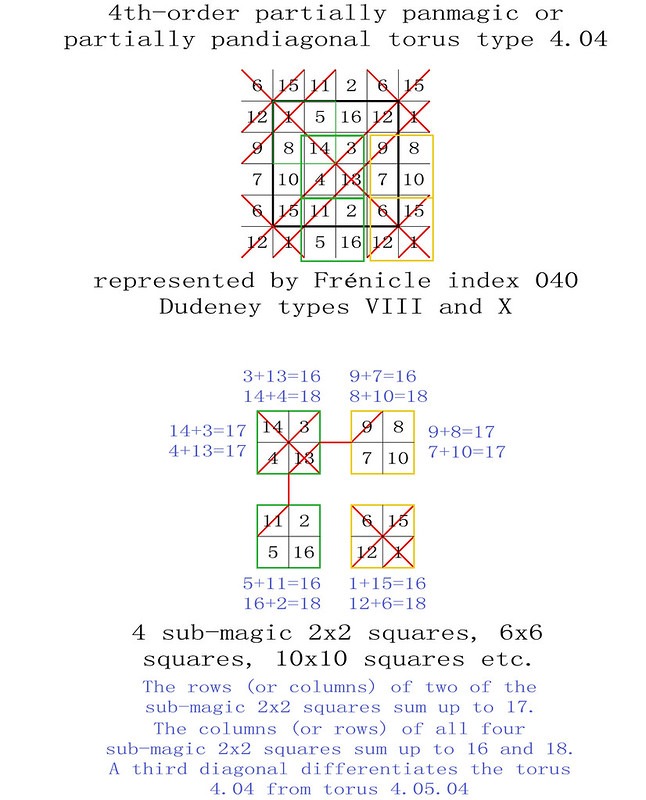
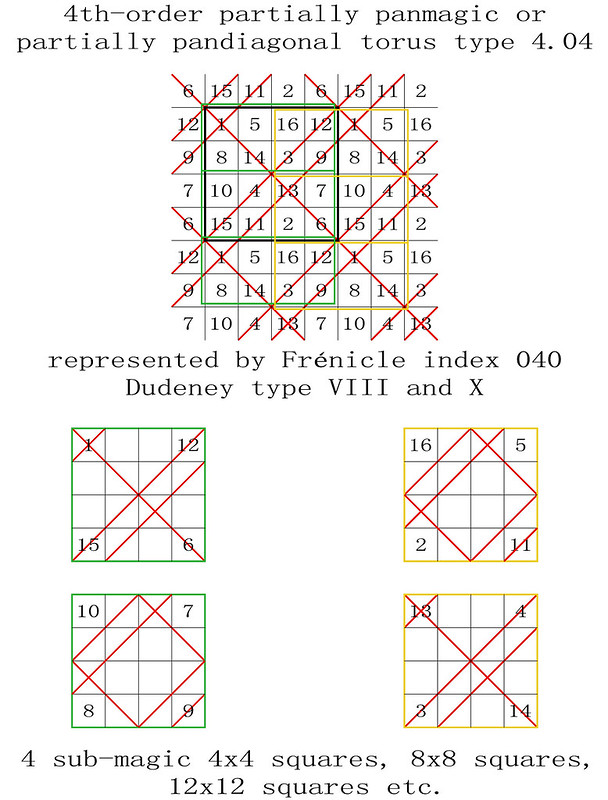
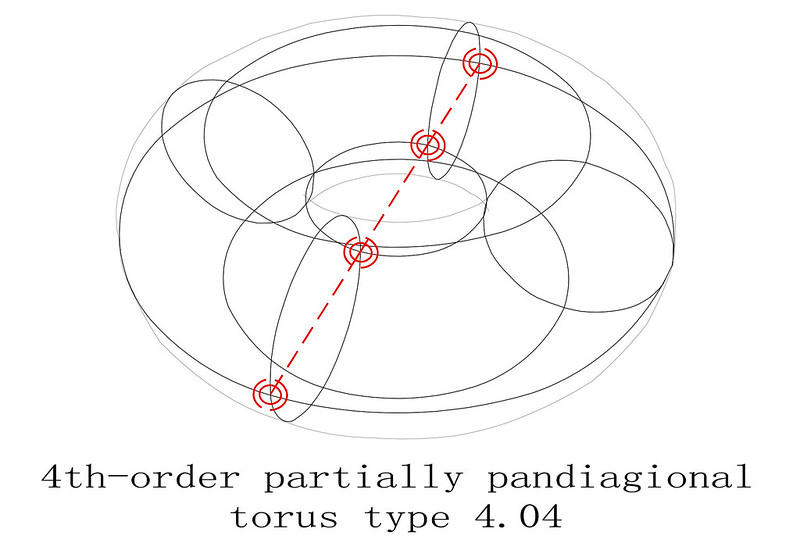
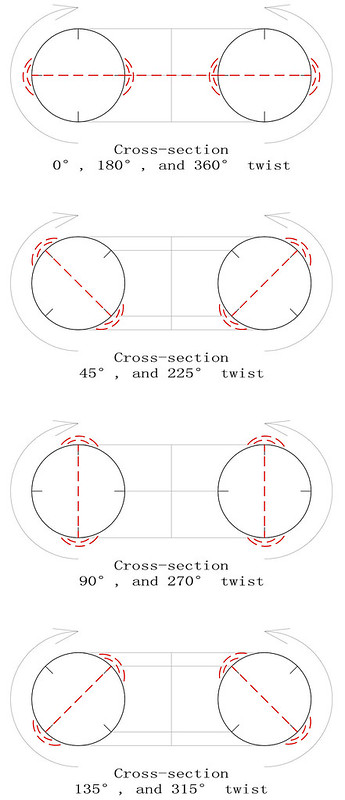
Finding the torus-opposite pairs of magic squares in even-orders:
The following diagram, which illustrates the array of n² essentially-different square viewpoints of a basic magic torus of order-n, starting here with the 4x4 magic square that has the Frénicle index n° 1, shows how a torus-opposite magic square of order-4 can be identified:
 |
| Array of 16 essentially-different square viewpoints of a basic magic torus of order-4 |
This basic magic torus, now designated as type n° T4.05.1.01, can be seen to display a torus-opposite pair of Frénicle-indexed magic squares n° 1-458 (with Dudeney pattern VI), as well as 7 torus-opposite pairs of semi-magic squares that the discerning reader will easily be able to spot.
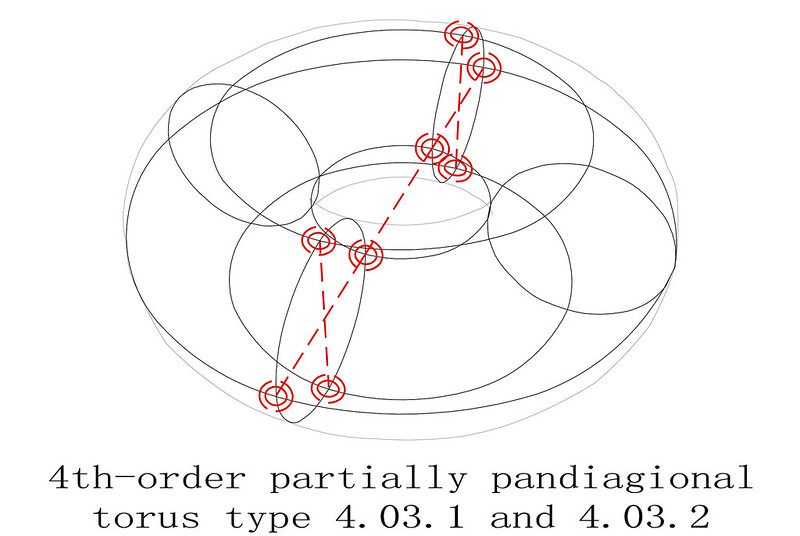
The relative positions of the numbers of torus-opposite squares can be expressed by a simple plus or minus vector. There are always two equal shortest paths towards the far side of the torus: These are, in toroidal directions, east or west along the latitudes, and in poloidal directions, north or south along the longitudes of the doubly-curved 2D surface. So, if the even-order is n, then:
v = ( ± n/2, ± n/2 )
 |
| "Tesseract Torus" by Tilman Piesk CC-BY-4.0 https://commons.wikimedia.org/w/index.php?curid=101975795 |
Torus-opposite squares are not just limited to basic magic tori, as they also exist on pandiagonal, semi-pandiagonal, partially pandiagonal, and even semi-magic tori of even-orders. Therefore, for order-4, we can either say that there are 880 magic squares, or we can announce that there are 440 torus-opposite pairs of magic squares. Similarly, the 67,808 semi-magic squares of order-4 can be expressed as 33,904 torus-opposite pairs of semi-magic squares, etc.
Why torus-opposite pairs of magic squares cannot exist in odd-orders
A torus-opposite magic square always exists in even-orders because an even-order magic square has magic diagonals that produce a first magic intersection at a centre between numbers, and another magic intersection at a second centre between numbers on the far side of the torus (at the meeting point of the four corners of the first magic square viewpoint). However, in odd-orders, where a magic square has magic diagonals that produce a magic intersection over a number, then a sterile non-magic intersection always occurs between numbers on the far side of the torus (at the meeting point of the four corners of the initial magic square). This is why torus-opposite pairs of magic squares cannot exist in the odd-orders.
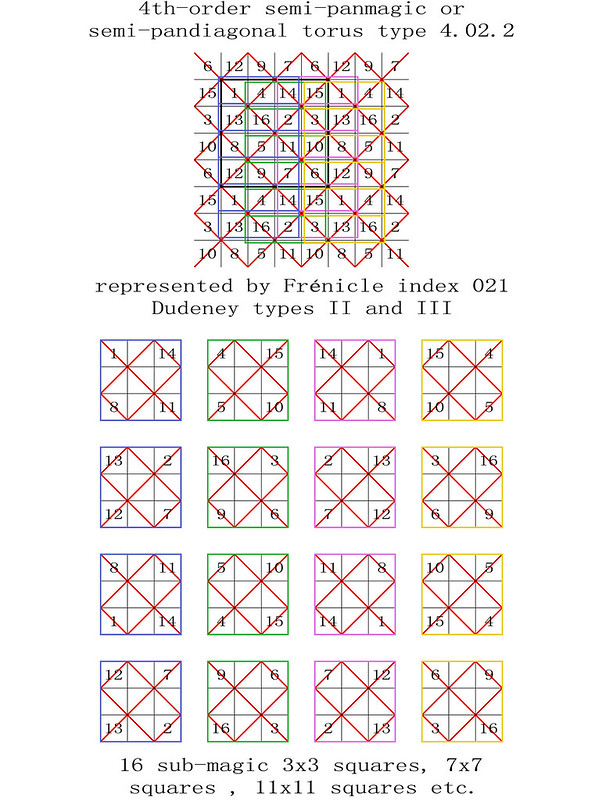
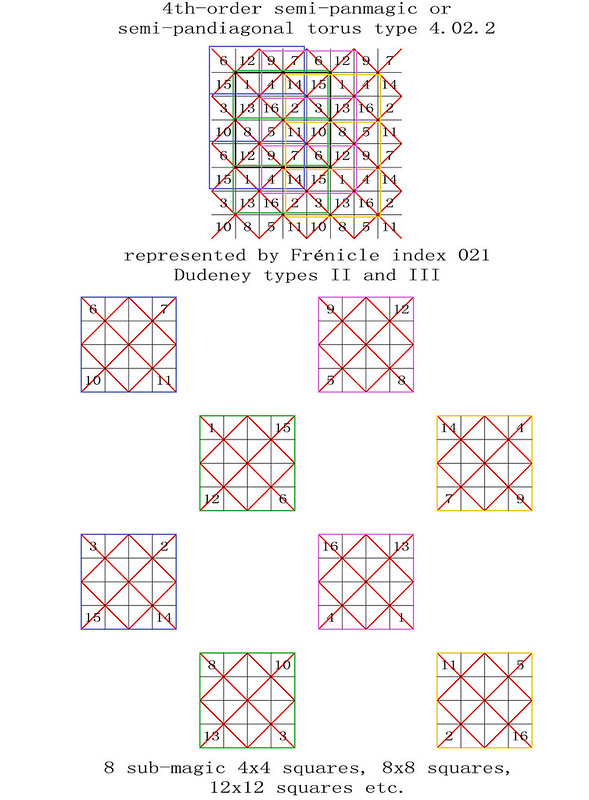
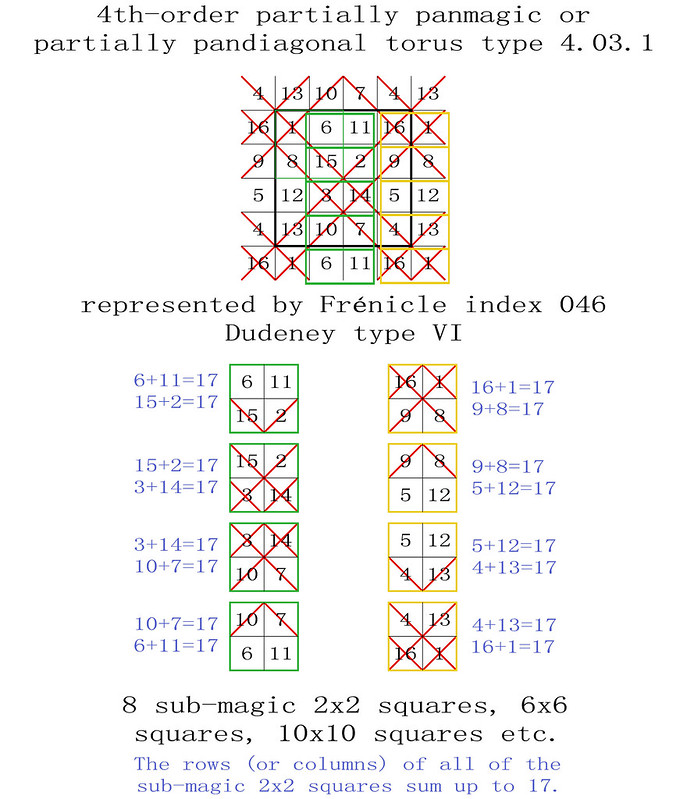
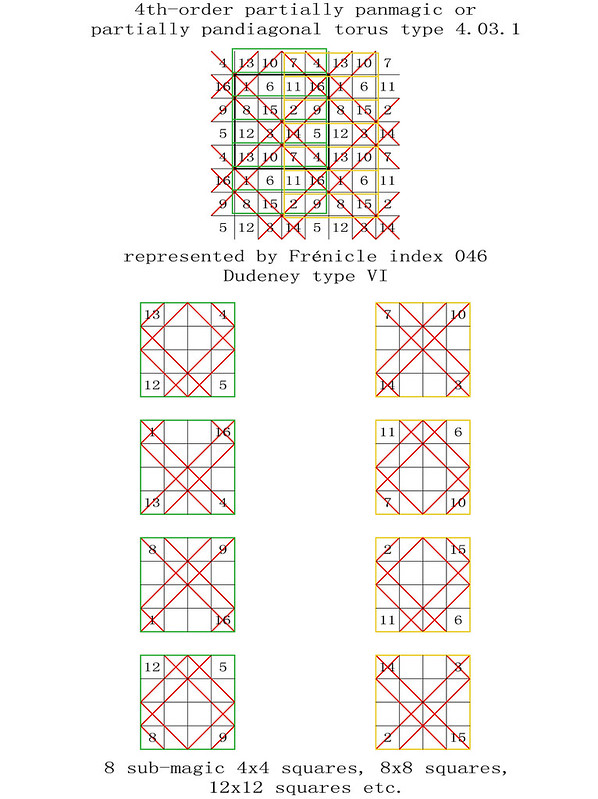
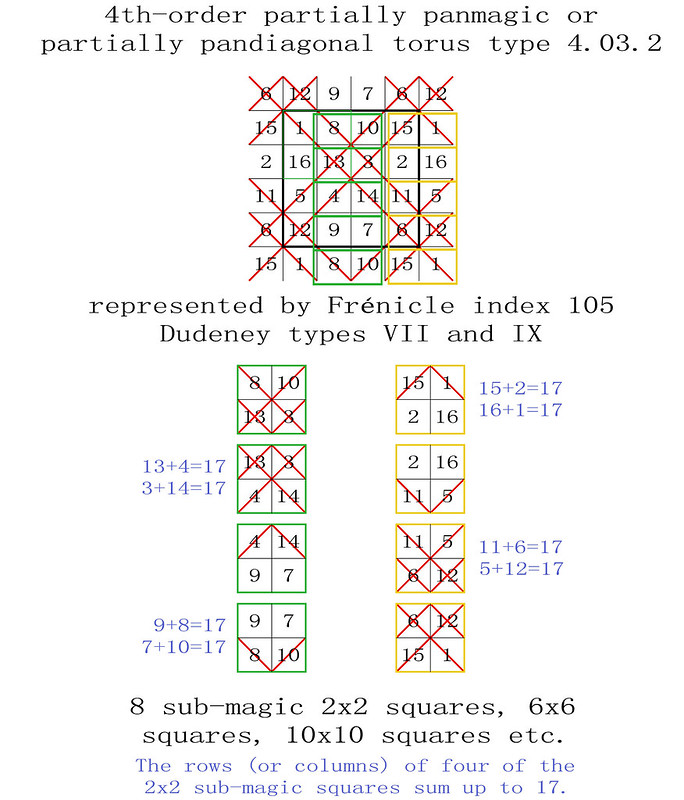
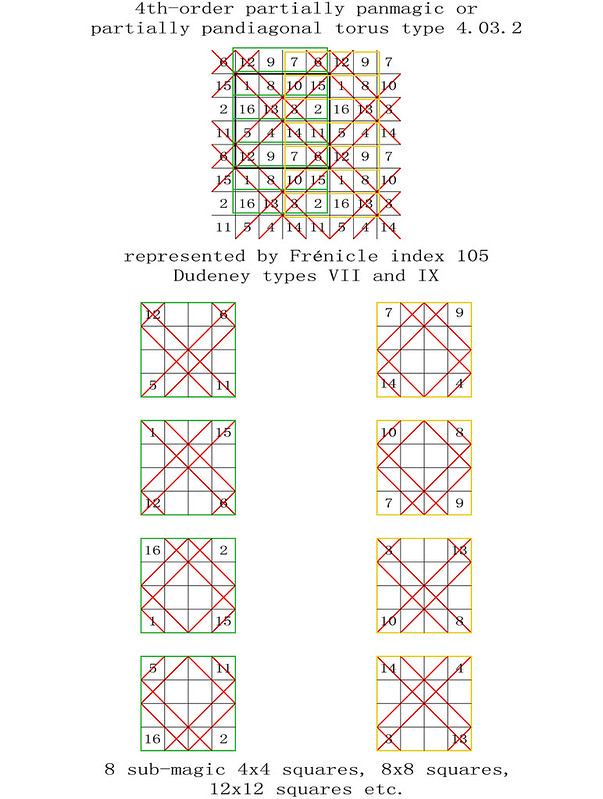
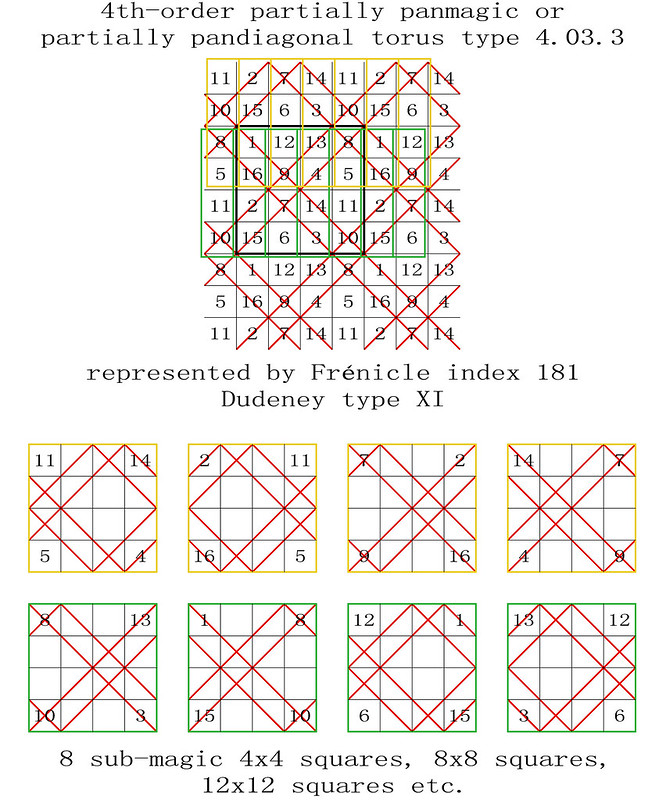
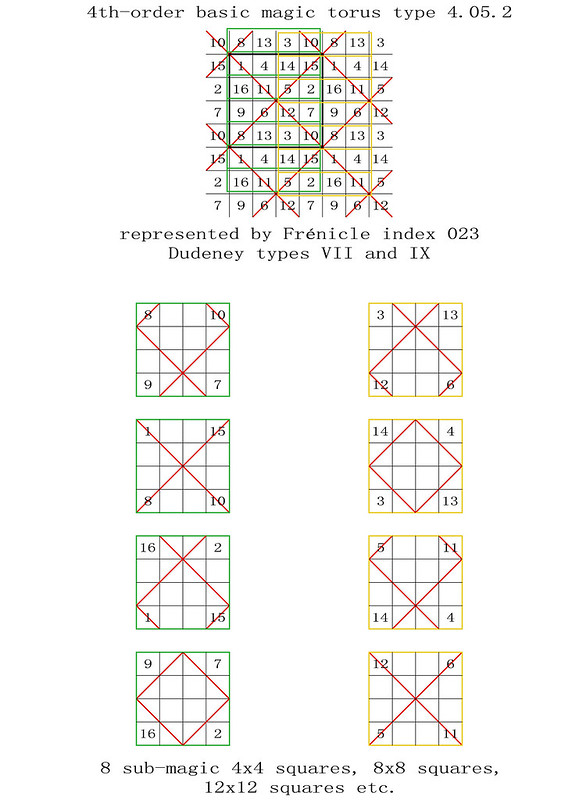
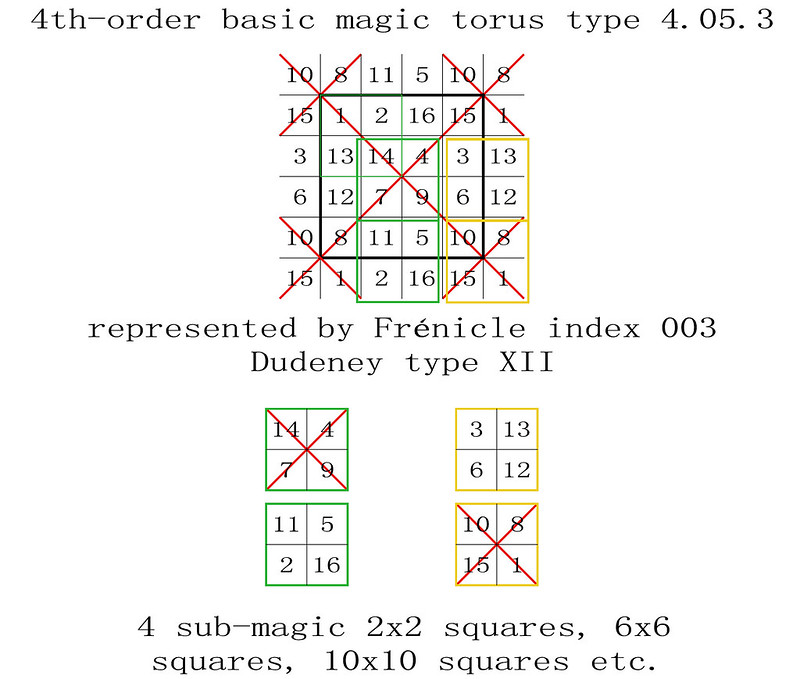
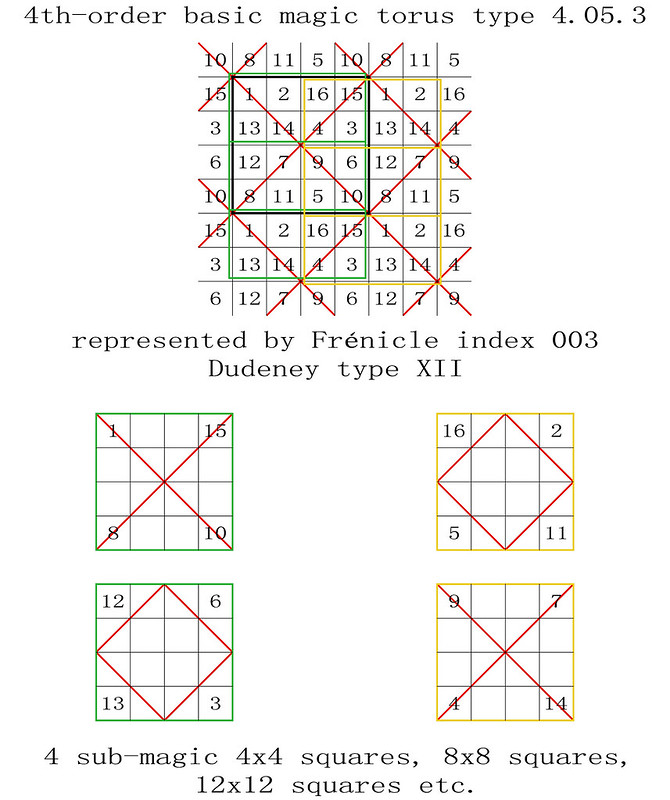
255 magic tori of order-4, listed by type, with details of the 440 torus-opposite pairs of the 880 Frénicle magic squares of order-4
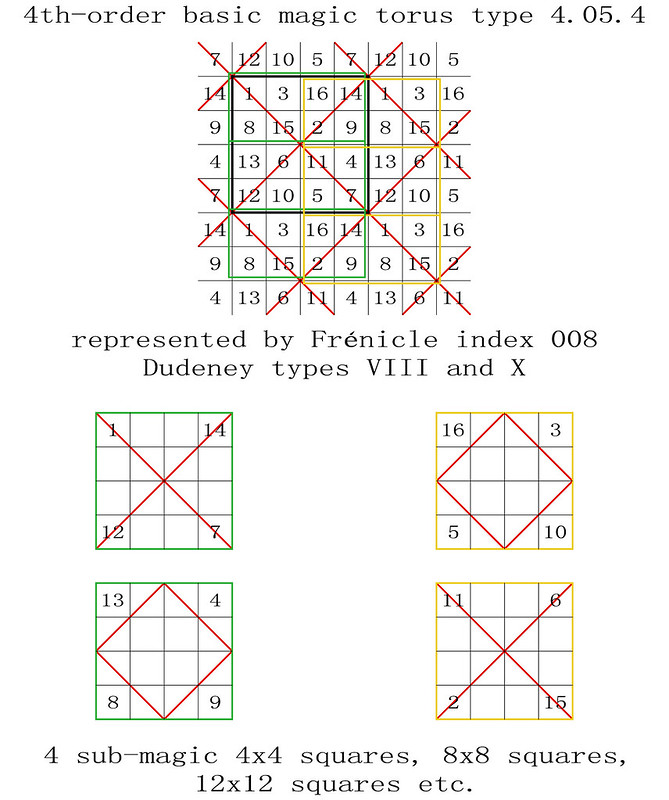
The enumeration of the 255 magic tori of order-4 was first published in French on the 28th October 2011, before being translated into English on the 9th January 2012: "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus." In this previous article, the corresponding 880 fourth-order magic squares were listed by their Frénicle index numbers, but not always illustrated. The intention of the enclosed paper is therefore to facilitate the understanding of the magic tori of order-4, by portraying each case.
Here, Frénicle index numbers continue to be used, as they have the double advantage of being both well known and commonly accepted for cross-reference purposes. But please also note, that now, in order to simplify the visualisation of the magic tori, their displayed magic squares are not systematically presented in Frénicle standard form.
In the illustrations of the 255 magic tori of order-4, listed by type with the presentation of their magic squares, the latter are labelled from left to right with their Frénicle index number, followed by, in brackets, the Frénicle index number of their torus-opposite magic square, and finally by the Roman numeral of their Dudeney complementary number pattern. Therefore, for the magic square of order-4 with Frénicle index n° 1 (that forms a torus-opposite pair of magic squares with Frénicle index n° 458; both squares having the same Dudeney pattern VI), its label is 1 (458) VI.
To find the "255 magic tori of order-4, listed by type, with details of the 440 torus-opposite pairs of the 880 Frénicle magic squares of order-4" please consult the following PDF: