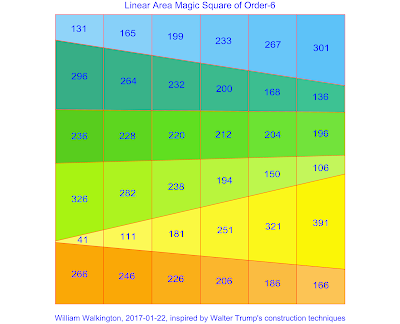
For the area magic square shown above, the magic constant of each row, column and main diagonal is 1296 (64). The total areas are therefore 7776 (65). The mean number of each row, column and main diagonal is 216 (63). The last digits of the first and last numbers of the horizontal non-parallel rows are either 1 for odd number sequences, or 6 for even number sequences. Please note that the area cell 41 is not a triangle, but a trapezium (or trapezoid) like all the other cells. For those amongst you who may be interested in the mathematical construction, Hans-Bernhard Meyer has since very kindly produced the following parameterisation:
On the 29th January 2017, Hans-Bernhard Meyer informed me that the following can be proved:
Every 6x6 L-AMS with magic sum S and horizontal centre line has the property:
x04+x11+x18+x19+x26+x33 = x03+x08+x13+x24+x29+x34 = S
and conversely, every 6x6 L-AMS with magic sum S and
x04+x11+x18+x19+x26+x33 = x03+x08+x13+x24+x29+x34 = S
has a horizontal centre line.
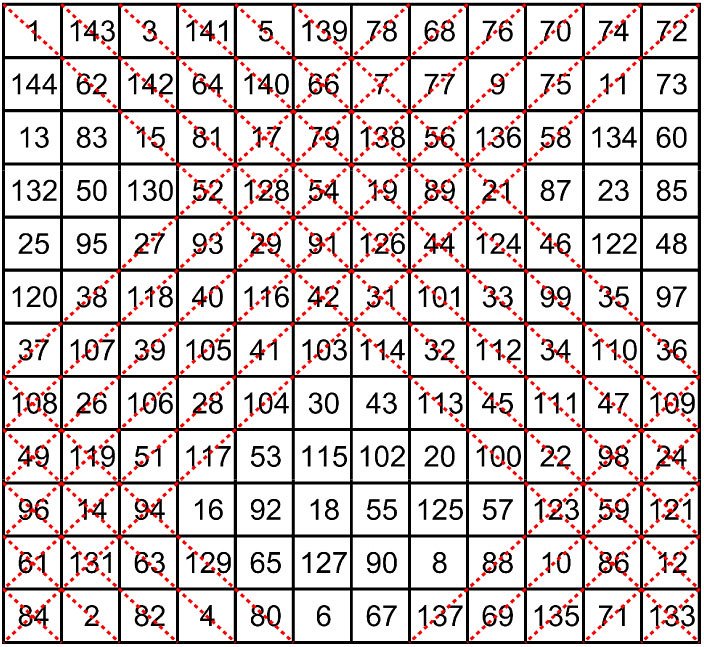
He stated that there are many examples of such L-AMS and strongly supposed that the example illustrated above had the lowest possible magic sum. He was able to confirm that examples with 2 horizontal lines do not exist.
On the same day, Hans-Bernhard also informed me that in the order-6, the L-AMS with the lowest possible magic sum had a magic constant of 402. He had found that there were several of these L-AMS, and kindly sent me details of an example, which I have illustrated below:
Related links
A former post Area Magic Squares and Tori of Order-3 can be found in these pages since the 13th January 2017.
On the 25th January 2017, Hans-Bernhard Meyer published an article entitled Observations on 4x4 Area Magic Squares with vertical lines in his website: Math'-pages.
On the 3rd February 2017, Walter Trump published a chapter entitled Area Magic Squares in his website: Notes on Magic Squares. This chapter includes many analyses and examples of area magic squares of the third and fourth-orders.
Since the 8th February 2017, "Area Magic Squares of Order-4" relates the first findings of area magic squares of the fourth-order.
In the N° 487 2018 May issue of "Pour La Science" (the French edition of Scientific American), Professor Jean-Paul Delahaye has written an article entitled "Les Carrés Magiques d'Aires."
In the December 2018 issue of "Spektrum der Wissenschaft" (a Springer Nature journal, and the German edition of Scientific American), Professor Jean-Paul Delahaye has written an article entitled "FLÄCHENMAGISCHE QUADRATE."