Further to my last article (published on the 26th March) Harry White has kindly run a computer programme to verify and validate my hypothesis: The 4th-order magic tori are indeed totally covered by sub-magic 2x2 squares.
As Harry White's results gave 7,712 sub-squares for the 880 Frénicle squares it was necessary to determine which tori had a reduced cover of sub-magic squares. After verification I have found that there are two families of the type 2 and type 5 tori. My latest results and totals are given below. It could be that by using observation and manual input I have overlooked something. Your comments are always welcome.
4th-order panmagic or pandiagonal torus type 4.01
 |
| 4th-order panmagic or pandiagonal torus type 4.01 represented by Frénicle index 102, Dudeney type I |
 |
| 4th-order panmagic or pandiagonal torus type 4.01 represented by 16 sub-magic 2x2 squares |
4th-order semi-panmagic or semi-pandiagonal torus type 4.02.1
 |
| 4th-order semi-panmagic or semi-pandiagonal torus type 4.02.1 represented by Frénicle index 016, Dudeney type VI |
 |
| 4th-order panmagic or pandiagonal torus type 4.02.1 represented by 12 sub-magic 2x2 squares |
4th-order semi-panmagic or semi-pandiagonal torus type 4.02.2
 |
| 4th-order semi-panmagic or semi-pandiagonal torus type 4.02.2 represented by Frénicle index 021, Dudeney type II |
 |
| 4th-order semi-panmagic or semi-pandiagonal torus type 4.02.2 represented by 8 sub-magic 2x2 squares |
4th-order partially panmagic or partially pandiagonal torus type 4.03
 |
| 4th-order partially panmagic or partially pandiagonal torus type 4.03 represented by Frénicle index 046, Dudeney type VI "Simple" |
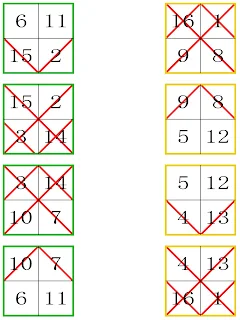 |
| 4th-order partially panmagic or partially pandiagonal torus type 4.03 represented by 8 sub-magic 2x2 squares |
4th-order partially panmagic or partially pandiagonal torus type 4.04
 |
| 4th-order partially panmagic or partially pandiagonal torus type 4.04 represented by Frénicle index 040, Dudeney type VIII "Simple" |
 |
| 4th-order partially panmagic or partially pandiagonal torus type 4.04 represented by 4 sub-magic 2x2 squares |
4th-order basic magic torus type 4.05.1
 |
| 4th-order basic magic torus type 4.05.1 represented by Frénicle index 002, Dudeney type VI Simple |
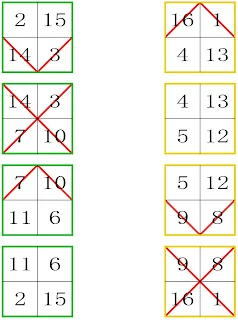 |
4th-order basic magic torus type 4.05.1 represented by 8 sub-magic 2x2 squares |
4th-order basic magic torus type 4.05.2
 |
| 4th-order basic magic torus type 4.05.2 represented by Frénicle index 003, Dudeney type XII Simple |
 |
| 4th-order basic magic torus type 4.05.2 represented by 4 sub-magic 2x2 squares |
Conclusion:
Each number of a fourth-order magic torus (or magic square) comes from at least one 2x2 sub-magic square. Or, expressed otherwise, the surface of every fourth-order magic torus is entirely covered by 2x2 sub-magic squares. This hypothesis has since been confirmed by Harry White's computer skills (see above).
Please note that I have published a new article that extends the above findings.
The table below is a new résumé of the different 4th-order magic tori taking into account the different arrangements of the sub-magic 2x2 squares that cover them.



No comments:
Post a Comment
Or, should you prefer to send a private message, please email william.walkington@wandoo.fr