Alignment and Concentricity of Sub-Magic Squares on 4th-Order Magic Tori

Once the sub-magic 2x2 squares were found I remembered having seen traces of larger sub-magic squares when studying the 4th-order panmagic torus. I therefore decided to search for these larger sub-magic squares on the different types of 4th-order magic tori. 

Since a first edition on the 17th April 2013, I have updated this article on the 21st April 2013, adding subdivisions of the tori to take into account the different Dudeney types.

I have not verified every Frénicle square, and the results illustrated below are based on simple observation and manual input. Your comments are always welcome! 

At the end of this article I propose some new hypotheses.

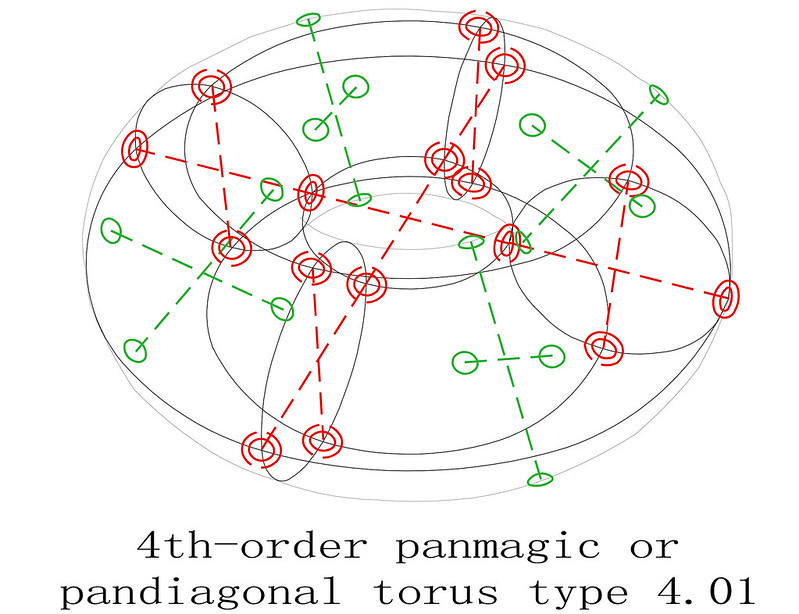
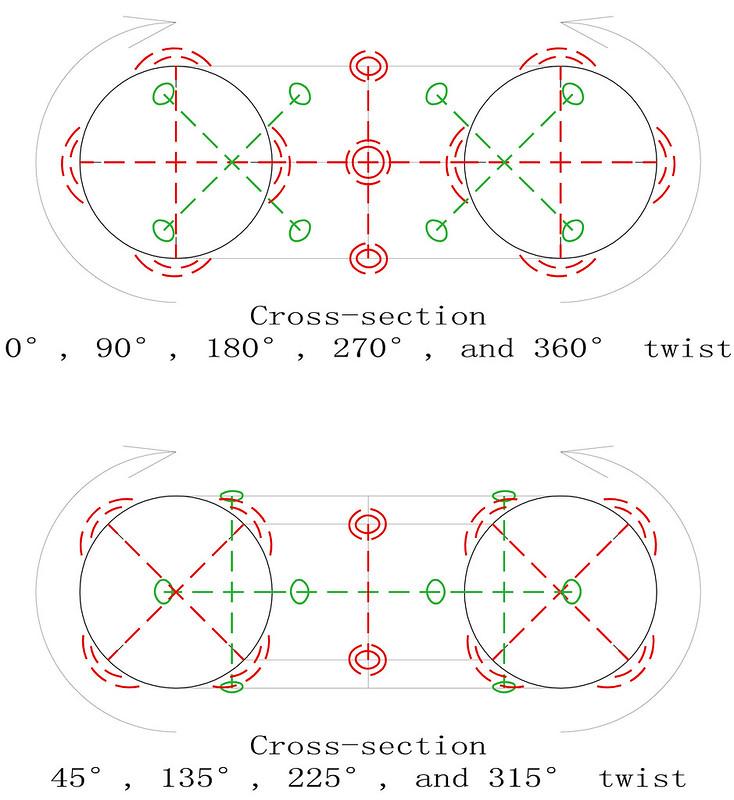
4th-order pandiagonal torus type T4.01

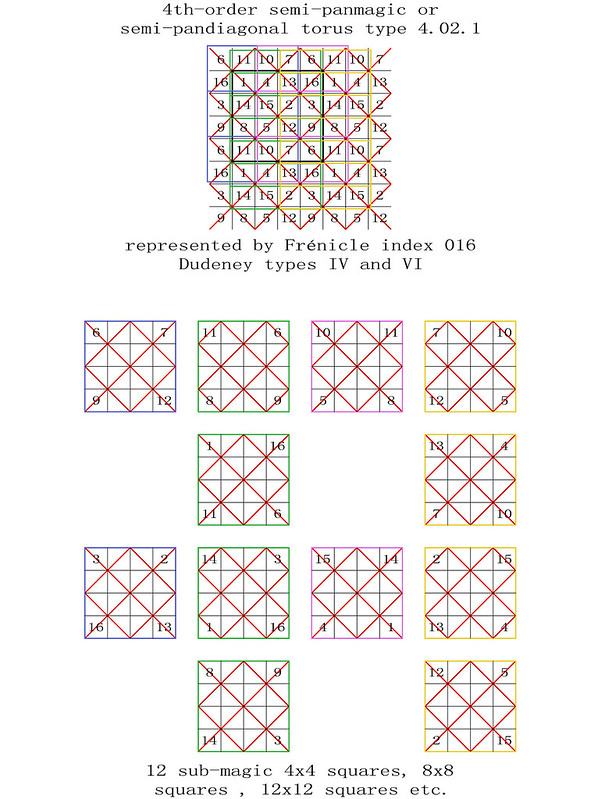
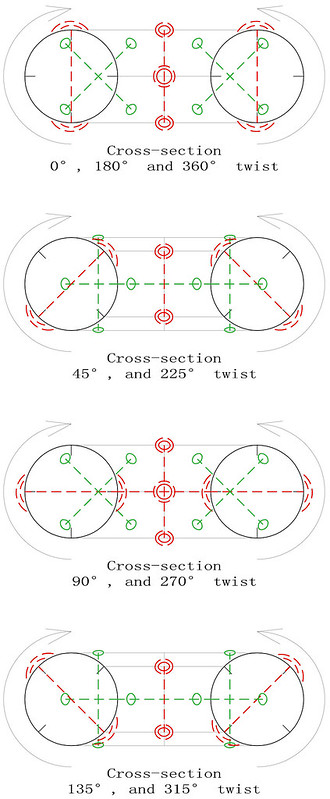
4th-order semi-pandiagonal torus type T4.02.1

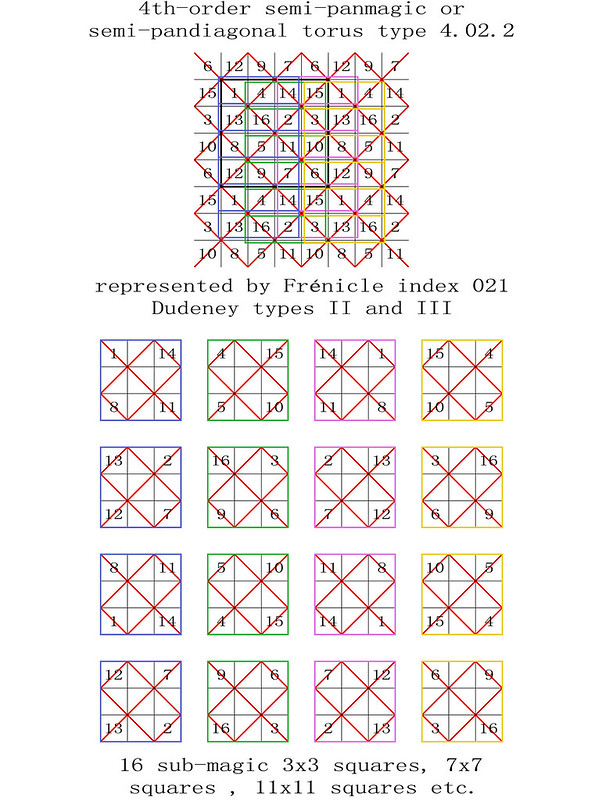
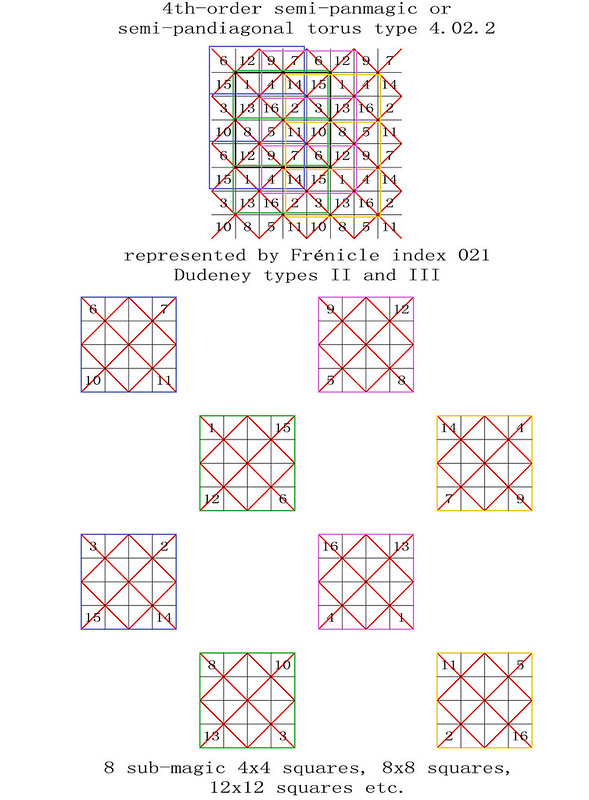
4th-order semi-pandiagonal torus type T4.02.2

For recreational water retention studies on associative magic squares, such as those displayed on the tori type T4.02.2 illustrated above, please refer to Craig Knecht's article in Wikipedia.

 

4th-order semi-pandiagonal torus type T4.02.3

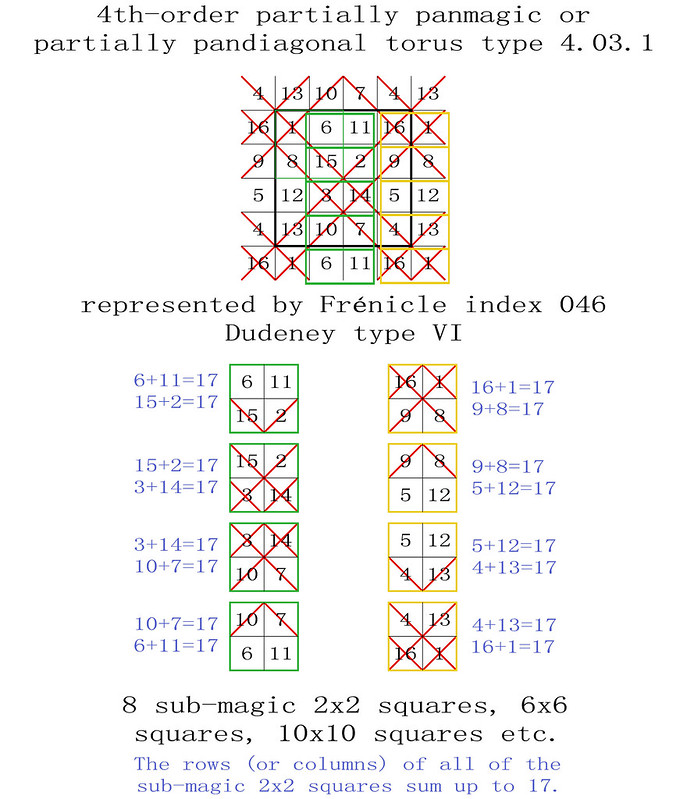
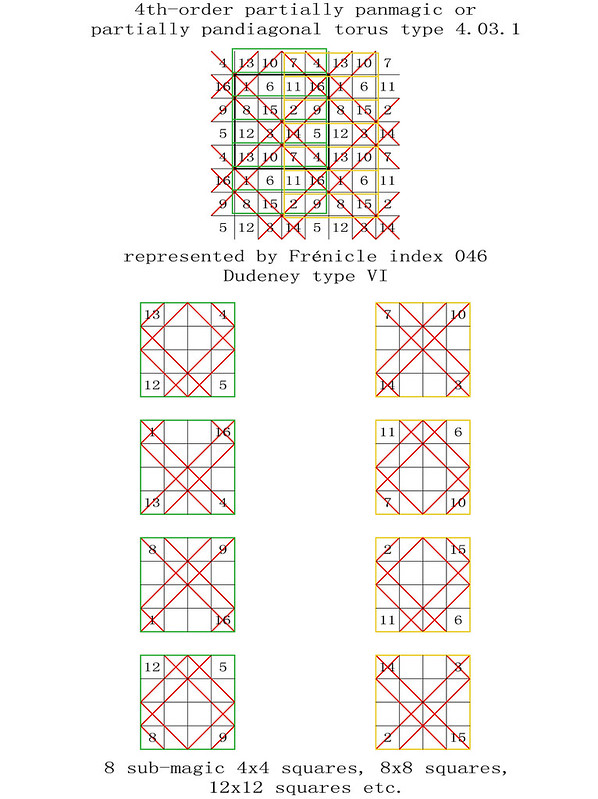
4th-order partially panmagic torus type T4.03.1

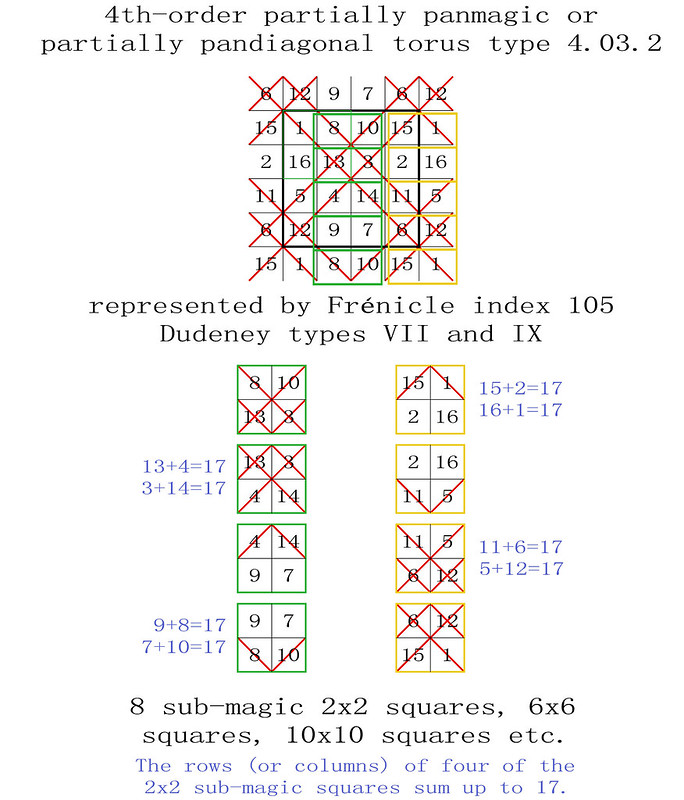
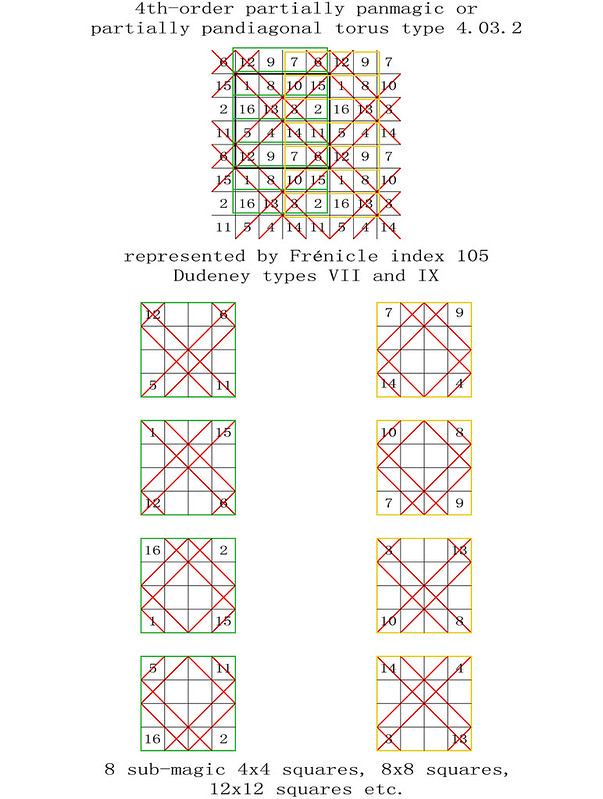
4th-order partially panmagic torus type T4.03.2

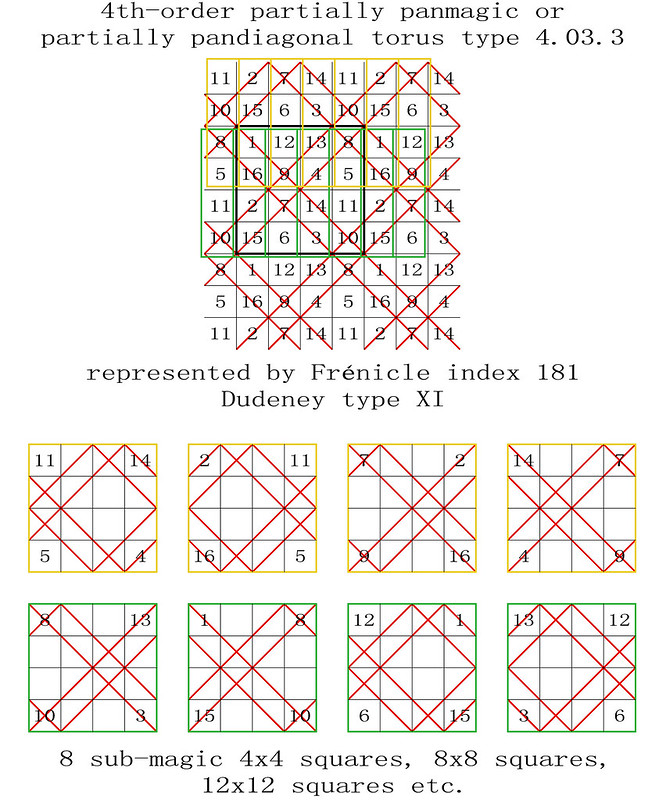
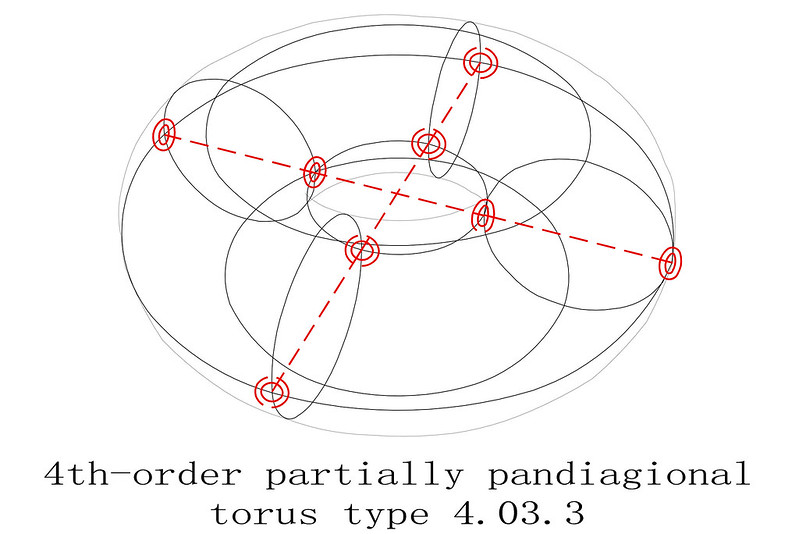
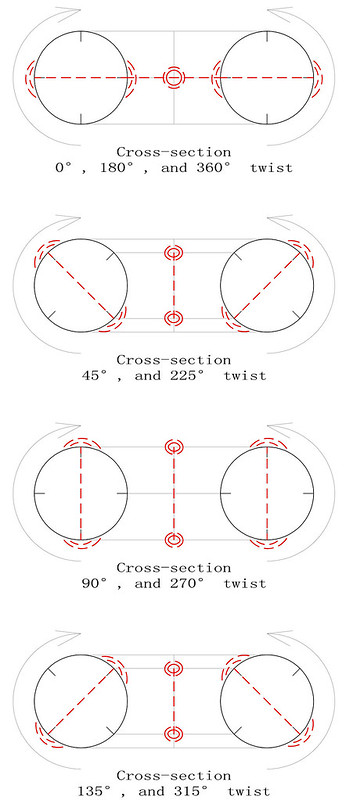
4th-order partially panmagic torus type T4.03.3

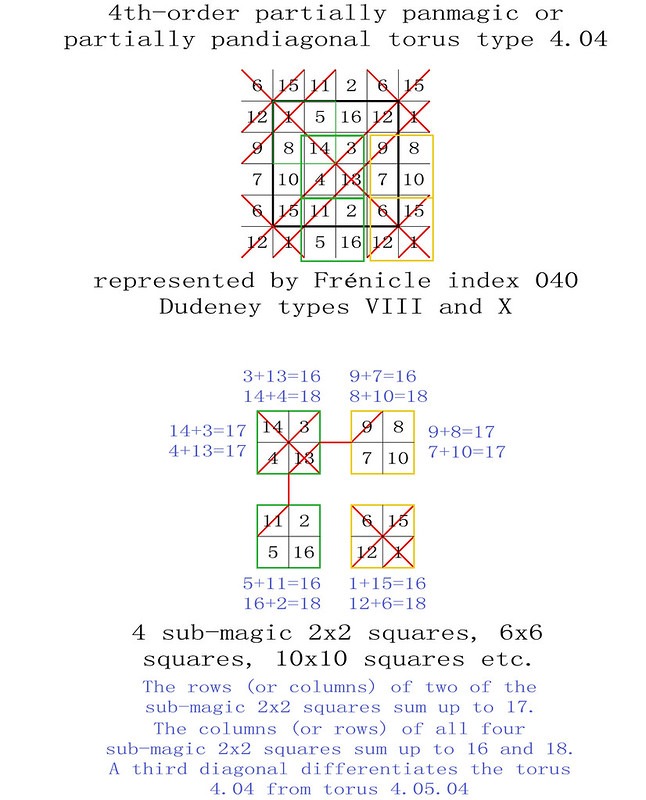
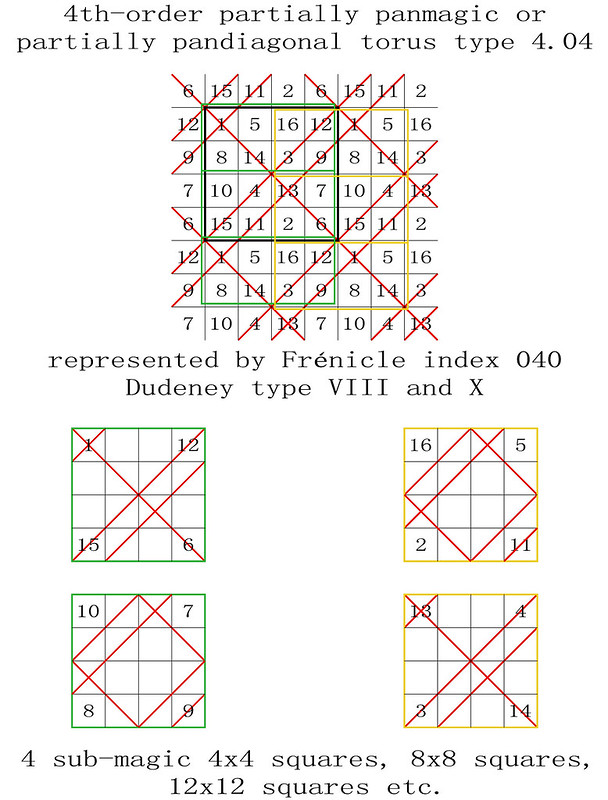
4th-order partially panmagic torus type T4.04

4th-order basic magic torus type T4.05.1

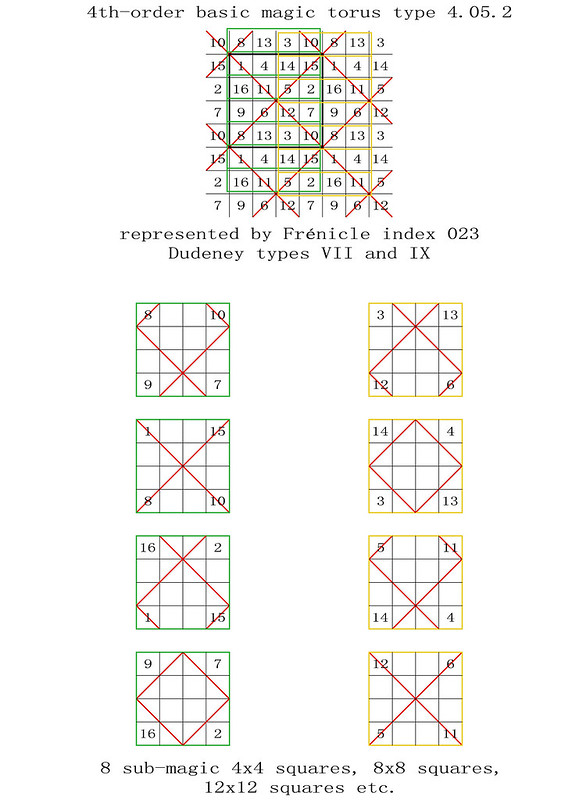
4th-order basic magic torus type T4.05.2

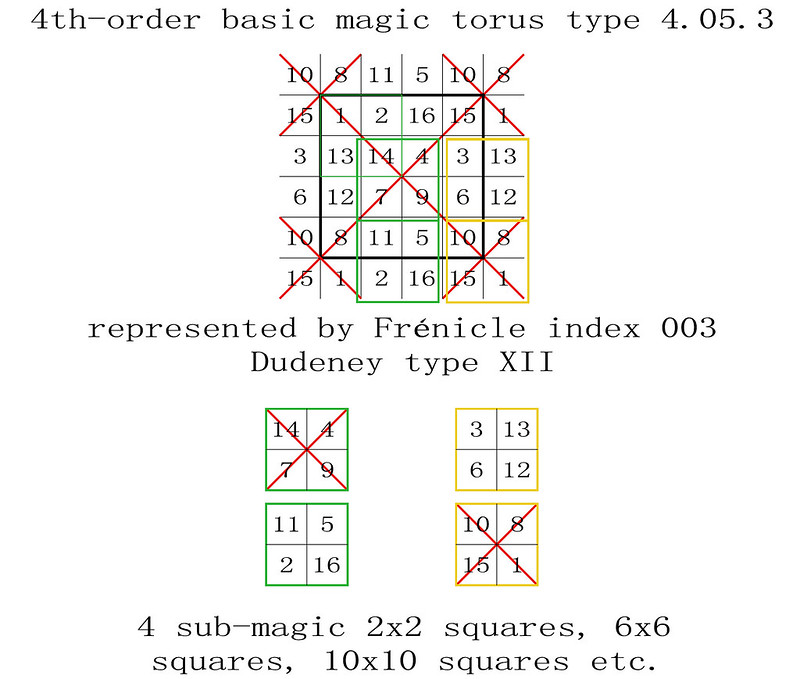
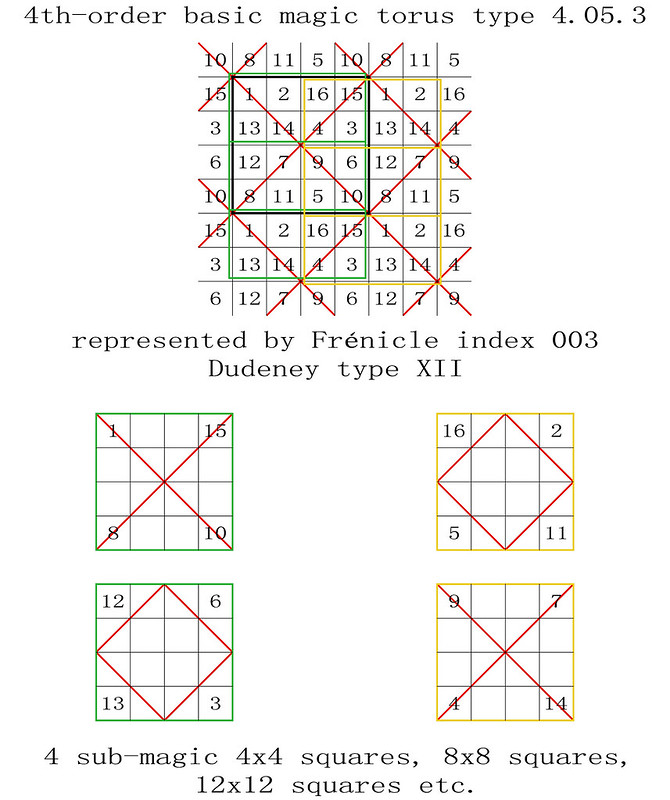
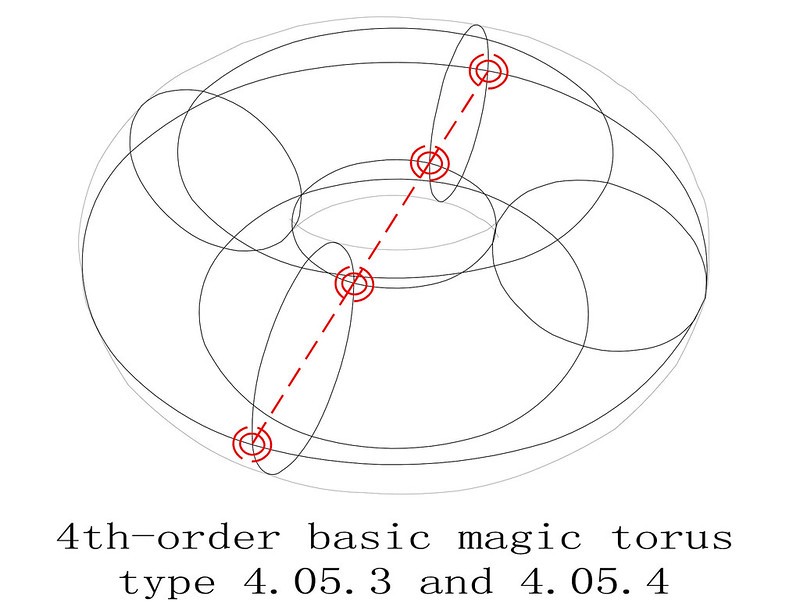
4th-order basic magic torus type T4.05.3

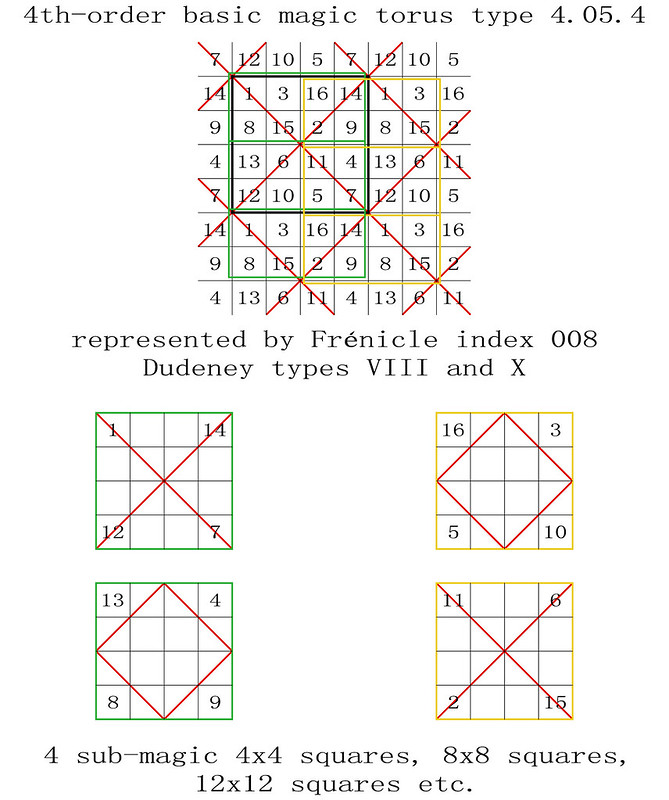
  4th-order basic magic torus type T4.05.04

Observations

Although magic rows, columns and diagonals are important, it seems that the sub-magic squares are a driving force of the 4th-order magic tori.

The number patterns and quantities of 2x2 and 4x4 sub-magic squares are identical. On 4th-order tori the corner numbers of a 2x2 sub-magic square always coincide with the corner numbers of a 4x4 sub-magic square and vice versa.

The T4.04 and the T5.03.4 tori are similarly constructed. The partially panmagic tori type T4.04 deserve a separate classification although their third diagonals do not produce magic intersections.

Apparently the sub-magic 3x3 squares are only displayed on panmagic and semi-panmagic tori. There seems to be a relationship between the spacing of magic diagonals and the presence of sub-magic 3x3 squares, and a one in two spacing of magic diagonals only occurs on the panmagic and semi-panmagic tori.

Whilst examining only magic tori when I first wrote this article, I thought that only the semi-magic tori with similarly spaced (but non-intersecting) diagonals such as the semi-magic tori type T4.06 and T4.08 would display sub-magic 3x3 squares. Dwane Campell has since demonstrated that sub-magic 3x3 squares are also displayed on the semi-magic tori type T4.10 without magic diagonals. Here are his examples:

The sub-magic 2x2 diamond shapes illustrated above were unknown to me until Dwane Campbell brought them to my attention. In his interesting web site article on 4th-order magic square classification he identifies the different cases of 2x2 diamond shapes on traditional Frénicle 4x4 squares.

Hypotheses

On 4th-order magic tori:

1/ Sub-magic 3x3 squares are only displayed on panmagic and semi-panmagic tori (or squares).

2/ Sub-magic 3x3 squares can be reduced to 4 essentially different subsquares per panmagic or per semi-panmagic torus. The addition of the central numbers of these essentially different sub-magic 3x3 squares totals 34.

3/ Sub-magic 2x2, 3x3, and 4x4 squares always display two even numbers and two odd numbers at their corners.

Developments

The discovery of the sub-magic 2x2 squares has inspired Mr Kanji Setsuda to make new studies of 4x4 squares, and a classification of standard magic squares by the 'composite conditions' of 2x2 squares within.