Third-Order Magic Torus T3

The first illustration shows a line path escaping from the boundaries of the traditional 3x3 magic square. The liberation of the line path is possible once we agree that magic squares are partial viewpoints of magic tori. This representation differs greatly from that of the traditional line path shown in the second illustration.

During the XVIIth century Claude-Gaspard Bachet de Méziriac (1581-1638) was the first to propose line paths that linked the numbers of magic squares in numerical order. The above illustration shows the line path of the traditional 3rd-order magic square "Saturn," previously associated with the astrological planet by Heinrich Cornelius Agrippa (1486-1535) in his "De occulta philosophia libri tres".

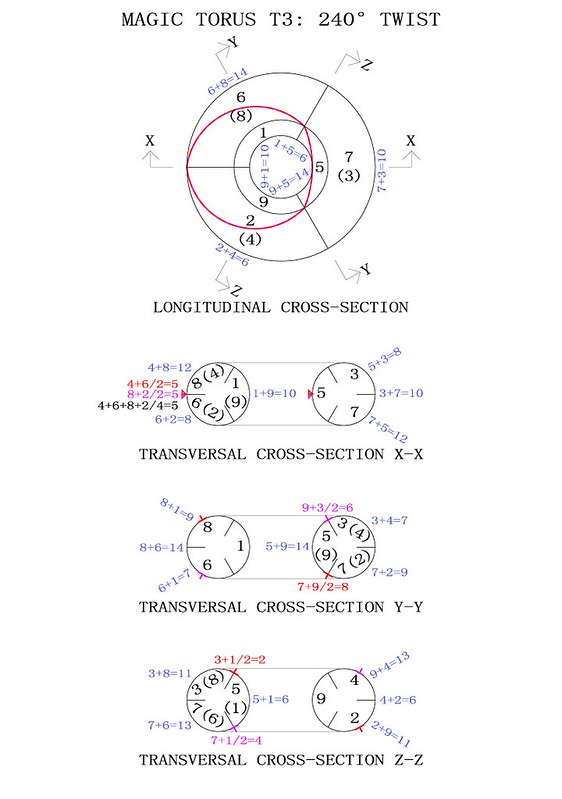
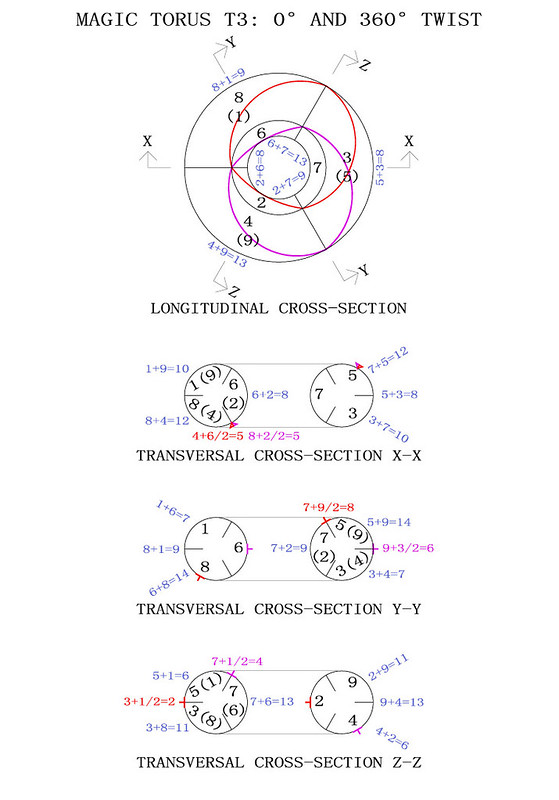
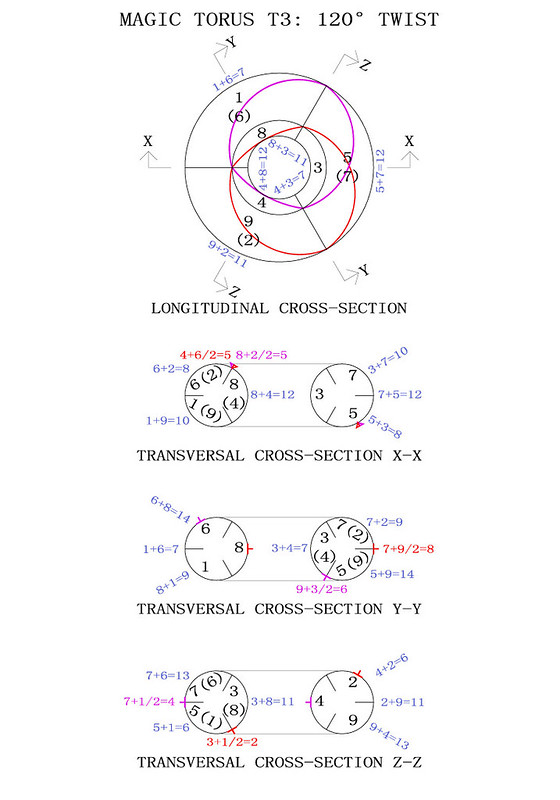
In order to better visualise how the T3 torus works I have produced the diagrams below. The magic torus is a symmetrically stable number system. When the torus is twisted through 360° different number couples produce continuously balanced tensions. I have indicated some of the mathematical properties but you will notice others when you contemplate this beautiful counting machine:

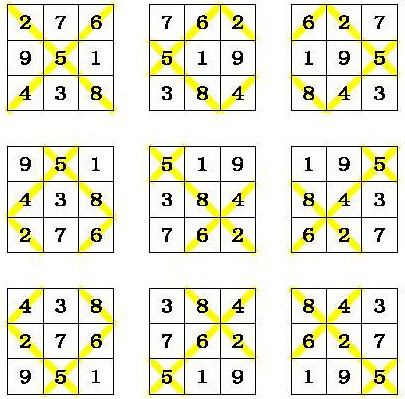
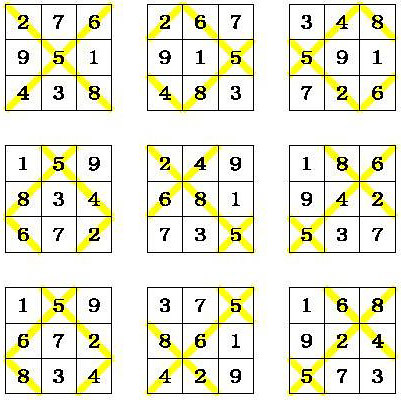
There are 9 squares on the 3rd order magic torus. Beginning with the 3x3 magic square in Frénicle standard form (at the top left of the following illustration), and taking into account the scrolling effect we obtain another eight 3rd-order semi-magic squares:

After transformation of these squares into Frénicle standard form we obtain:

The 3rd-order magic torus displays just one magic square. Although there are two crossed magic diagonals on the torus, they only produce a single magic intersection over the number 5, whilst the second intersection occurs in the interval between the numbers 6, 4, 8 and 2. It is interesting to note that the mean number of 6+4+8+2 is 5, and that the mean numbers of the couples 6+4 and 8+2 are also 5.