Fourth-Order Panmagic Torus T4.194

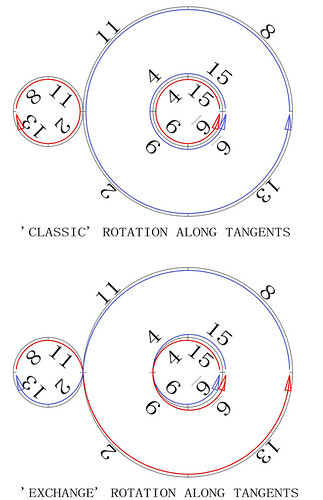
The illustration shows the interchangeability of horizontal or vertical representations of a same panmagic torus. By twisting one side of the interlocked torus the other side turns, and vice versa. A simultaneous twisting and turning movement is also possible. The contact between the two sides of the interlocked torus takes place along perpendicularly connected circular tangents.

Interlocked Pandiagonal Torus - (excluded from CC licence)

 What happens at the intersection of these tangents? Here are two ways of seeing things:

The interlocked magic torus could symbolise the interaction between opposites such as behind and in front, outside and inside, etc. Alternatively, if one side of the torus represents the past and the other the future, the present could take place along the two perpendicular circular tangents.

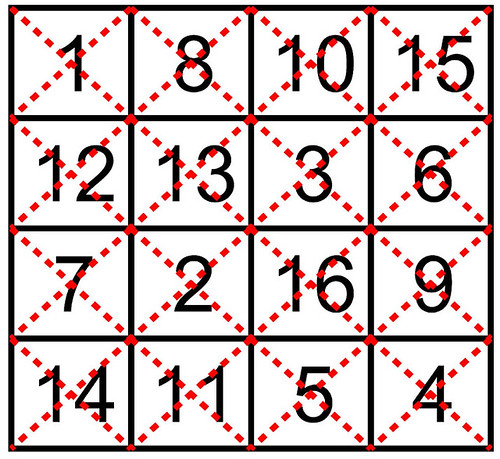
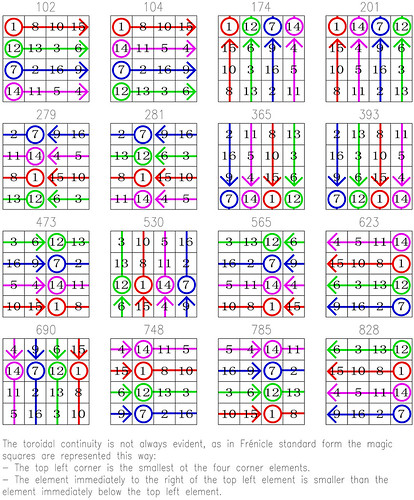
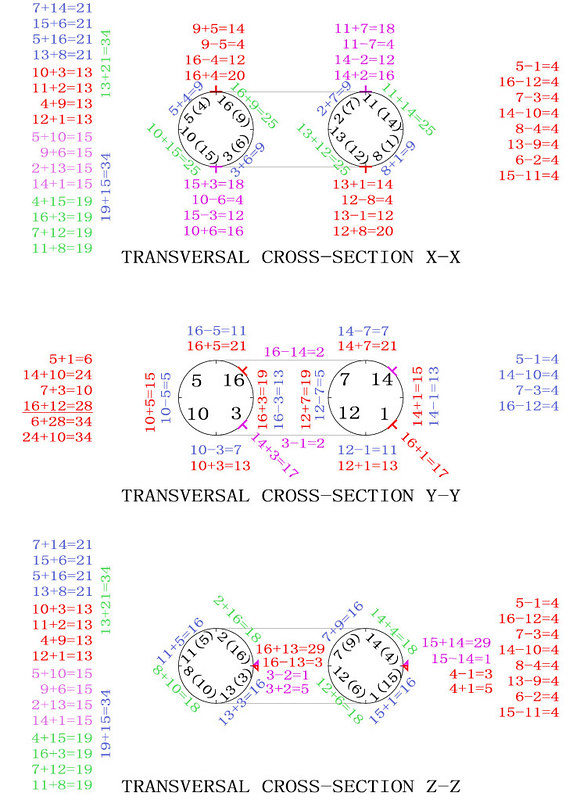
Leaving philosophical considerations, and returning to mathematics, the above illustration portrays a pandiagonal or panmagic torus classified by type n°T4.01.1 - see the previous article "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus" The torus displays 16 fourth-order pandiagonal squares (Frénicle index numbers 102, 104, 174, 201, 279, 281, 365, 393, 473, 530, 565, 623, 690, 748, 785, and 828). Since the publication of a new "Table of Fourth-Order Magic Tori" this torus is now also indexed and listed as the n° T4.194 in normalised square form:

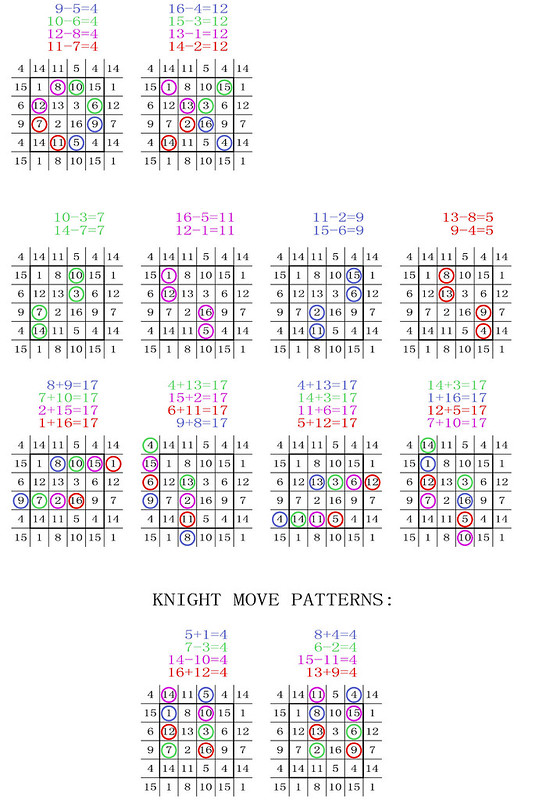
Numbered following the Bernard Frénicle de Bessy index, the pandiagonal squares that are displayed on this pandiagonal torus are as follows:  

The illustration below shows a way to spot the similar number sequences in the different Frénicle squares showing that they come from the same magic torus:

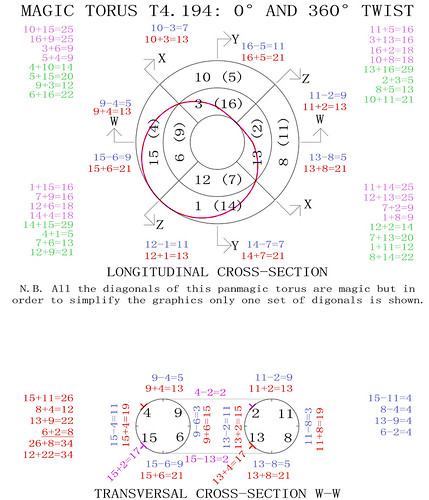
In order to better visualise how the T4.194 torus works I have produced the diagrams below. The magic torus is a symmetrically stable number system. When the torus is twisted through 360° changing number couples produce continuously balanced tensions. I have indicated some of the mathematical properties but you will notice others when you contemplate this beautiful counting machine. Further below, the results of the study are illustrated by patterns on the panmagic square.