Third-Order Magic Torus T3

The first illustration shows a line path escaping from the boundaries of the traditional 3x3 magic square. The liberation of the line path is possible once we agree that magic squares are partial viewpoints of magic tori. This representation differs greatly from that of the traditional line path shown in the second illustration.

During the XVIIth century Claude-Gaspard Bachet de Méziriac (1581-1638) was the first to propose line paths that linked the numbers of magic squares in numerical order. The above illustration shows the line path of the traditional 3rd-order magic square "Saturn," previously associated with the astrological planet by Heinrich Cornelius Agrippa (1486-1535) in his "De occulta philosophia libri tres".

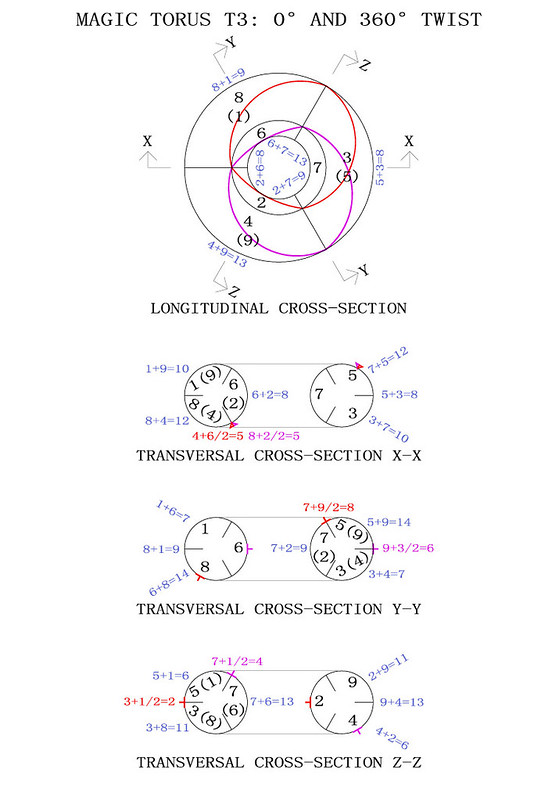
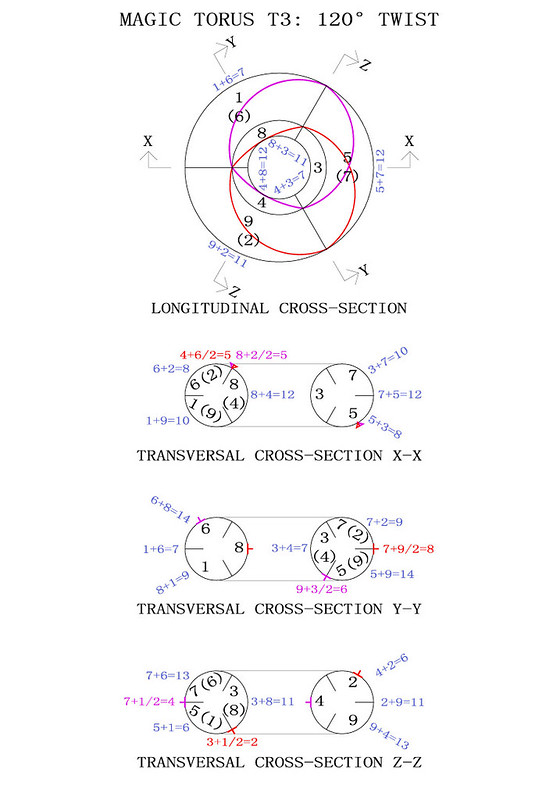
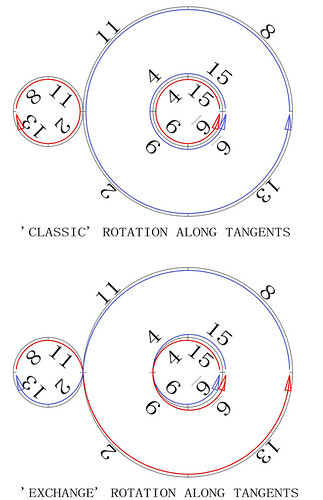
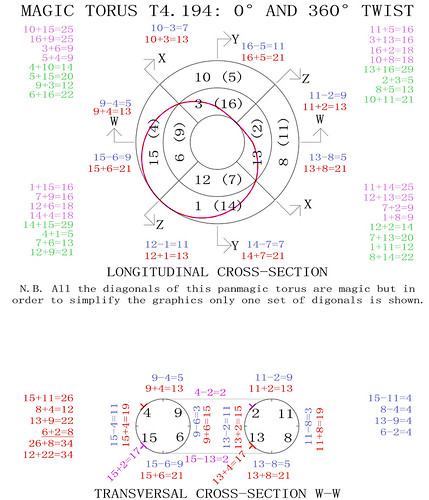
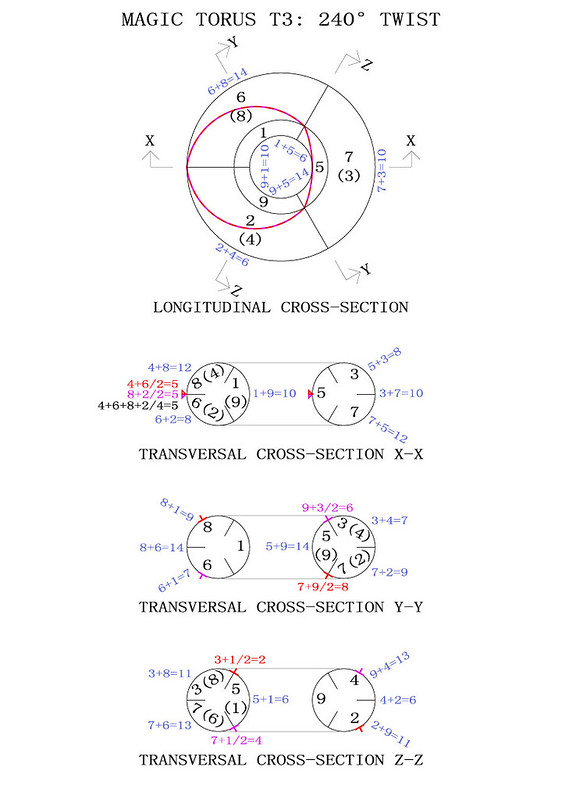
In order to better visualise how the T3 torus works I have produced the diagrams below. The magic torus is a symmetrically stable number system. When the torus is twisted through 360° different number couples produce continuously balanced tensions. I have indicated some of the mathematical properties but you will notice others when you contemplate this beautiful counting machine:

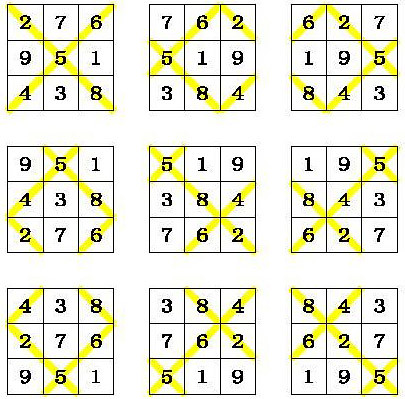
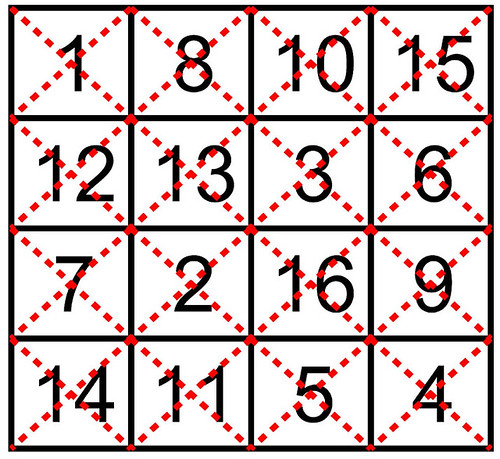
There are 9 squares on the 3rd order magic torus. Beginning with the 3x3 magic square in Frénicle standard form (at the top left of the following illustration), and taking into account the scrolling effect we obtain another eight 3rd-order semi-magic squares:

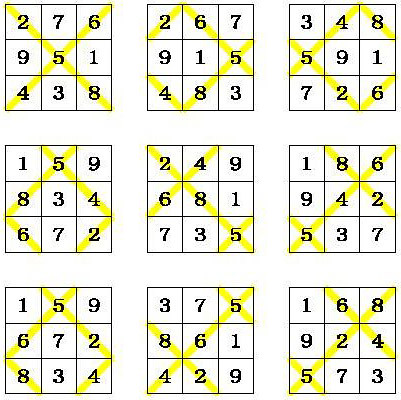
After transformation of these squares into Frénicle standard form we obtain:

The 3rd-order magic torus displays just one magic square. Although there are two crossed magic diagonals on the torus, they only produce a single magic intersection over the number 5, whilst the second intersection occurs in the interval between the numbers 6, 4, 8 and 2. It is interesting to note that the mean number of 6+4+8+2 is 5, and that the mean numbers of the couples 6+4 and 8+2 are also 5.

Read more ...

Fourth-Order Panmagic Torus T4.194

The illustration shows the interchangeability of horizontal or vertical representations of a same panmagic torus. By twisting one side of the interlocked torus the other side turns, and vice versa. A simultaneous twisting and turning movement is also possible. The contact between the two sides of the interlocked torus takes place along perpendicularly connected circular tangents.

Interlocked Pandiagonal Torus - (excluded from CC licence)

 What happens at the intersection of these tangents? Here are two ways of seeing things:

The interlocked magic torus could symbolise the interaction between opposites such as behind and in front, outside and inside, etc. Alternatively, if one side of the torus represents the past and the other the future, the present could take place along the two perpendicular circular tangents.

Leaving philosophical considerations, and returning to mathematics, the above illustration portrays a pandiagonal or panmagic torus classified by type n°T4.01.1 - see the previous article "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus" The torus displays 16 fourth-order pandiagonal squares (Frénicle index numbers 102, 104, 174, 201, 279, 281, 365, 393, 473, 530, 565, 623, 690, 748, 785, and 828). Since the publication of a new "Table of Fourth-Order Magic Tori" this torus is now also indexed and listed as the n° T4.194 in normalised square form:

Numbered following the Bernard Frénicle de Bessy index, the pandiagonal squares that are displayed on this pandiagonal torus are as follows:  

The illustration below shows a way to spot the similar number sequences in the different Frénicle squares showing that they come from the same magic torus:

In order to better visualise how the T4.194 torus works I have produced the diagrams below. The magic torus is a symmetrically stable number system. When the torus is twisted through 360° changing number couples produce continuously balanced tensions. I have indicated some of the mathematical properties but you will notice others when you contemplate this beautiful counting machine. Further below, the results of the study are illustrated by patterns on the panmagic square.

Read more ...

Table of Fourth-Order Magic Tori

In a previous article "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus," the 255 fourth-order magic tori have been identified and listed by type, following the numerical order of the Frénicle index numbers of the squares displayed on each torus. Although it was useful to begin this way, the classification by type is not practical when searching for a specific torus starting with any square.

I have therefore created an additional "Table of Fourth-Order Magic Tori" in which the 255 tori are also indexed and listed in numerical order for convenient reference. This table is, in a way, a homage to Bernard Frénicle de Bessy, as each torus is represented by a normalised square. The following illustration shows an example of the normalised square that represents the magic torus index n° T4.001 (type n° : T4.05.1.02), which displays not only 2 basic magic squares (Frénicle index numbers 2 and 448), but also 14 semi-magic squares:

The normalised squares are not necessarily traditional magic squares. Whether magic or semi-magic, they are just standard viewpoints of each magic torus. To see the other squares that are displayed by the torus, you need to displace the viewpoint, as explained in a previous article "From the Magic Square to the Magic Torus."

To view the complete "Table of Fourth-Order Magic Tori," please note that if you click on the button that appears at the top right hand side of the pdf viewer below, a new window will open and full size pages will then be displayed, with options for zooming.

Latest Developments

Further to studies published on the 28th March 2013, this table was revised on the 14th April 2013, to take into account the sub-magic 2x2 squares that are displayed on each torus, and then again on the 28th April 2013, to integrate new subdivisions that take into account different Dudeney types.

I wish to express my thanks to Aale de Winkel who pointed out an initial inversion of T4.003 and T4.004, which have since been interchanged to respect numerical order.

255 (the number of fourth-order magic tori) is now the fourth number of the sequence A270876 "Number of magic tori of order n composed of the numbers from 1 to n^2," published by the On-Line Encyclopedia of Integer Sequences (OEIS). 

Though the representation by normalised squares may not be ideal, it does give us a good insight of the subtle permutations that engender essentially different tori. The interrelationships of these tori are explored further and illustrated in an article "Multiplicative Magic Tori." published on the 21st January 2018. This post shows that the 255 magic tori of order-4 are different multiplied states of 82 Multiplicative Magic Tori (MMT) of order-4!

Since the 20th June 2019, twenty-seven of the 255 magic tori of order-4 are shown (using classic magic square geometry) to be Extra-Magic, having a parallel magic system with nodal intersections of 4 magic lines over numbers. These intersections do not yield traditional magic squares but are very significant for magic tori which have a limitless surface with no centre! Taking these findings into consideration, 136 of the 880 Frénicle-indexed magic squares are extra-magic! And when we take knight move magic diagonals into account, 6 intersecting magic lines can sometimes occur, and the total numbers of Extra-Magic Tori rise again! Since the 13th August 2019 a new article entitled "Extra-Magic Tori and Knight Move Magic Diagonals" confirms these findings and illustrates the different cases of extra-magic line intersections.

Since the 2nd September 2019, and the publication of a new article entitled "Even and Odd Number Patterns on Magic Tori of Orders 3 and 4", the Table of Fourth-Order Magic Tori is updated to include the details of the 4 essentially different even and odd number patterns.

Since the 24th April, 2024, a new article entitled "Plus or Minus Groups of Magic Tori of Order 4" now demonstrates that the 255 magic tori of order 4 (and the 880 magic squares that these tori display) originate from 137 plus or minus groups of order 4!
 

Read more ...