Complementary Number Patterns on Fourth-Order Magic Tori

The 880 fourth-order magic squares were first identified and listed by Bernard Frénicle de Bessy in his « Table générale des quarrez magiques de quatre, » which was published posthumously in 1693, in his book « Des quarrez magiques. » The census of these 880 4x4 squares is given in the appendix to the book « New Recreations With Magic Squares » by William H. Benson and Oswald Jacoby (Edition 1976), and also on the website of the late Harvey D. Heinz:  Frénicle n° 1 à 200, Frénicle n° 201 à 400, Frénicle n° 401 à 600, Frénicle n° 601 à 880.

Further to Bernard Frénicle de Bessy's initial findings, Henry Ernest Dudeney then classified the 880 fourth-order magic squares under 12 pattern types, in "The Queen" in 1910, (later republished in his book  "Amusements in Mathematics" in 1917). These patterns were determined through the observation of the relative positions of complementary pairs of numbers (which add up to N²+1 when N is the order of the square).

Although the different Dudeney pattern types can indeed be observed on fourth-order magic squares, they cannot be used for the classification of the fourth-order magic tori that display these squares. A Dudeney pattern type can be misleading because it depends on a bordered magic square viewpoint, whilst the magic torus that displays the magic square has a limitless surface...

In the study that follows the complementary number patterns are therefore tested, by comparing a developed torus surface and two traditional Frénicle magic square viewpoints for each of the 12 different types of fourth-order magic tori.

Complementary number patterns of each fourth-order magic torus type

General information on the magic torus index and type numbers

In addition to the Frénicle index numbers and the Dudeney types that have already been mentioned above, the present study also uses the index and type numbers of the fourth-order magic tori. For readers who may not be acquainted with the subject, essential information can be found in the following pages:

In a previous article "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus," the fourth-order magic tori have been classed in 12 types, and each magic torus has received a specific type number.

In a previous article "Table of Fourth-Order Magic Tori," so as to facilitate the identification of a magic torus beginning with any magic square, a standard torus form has also been defined, and each of the 255 fourth-order magic tori has received a specific index number.

Complementary number patterns of the pandiagonal tori type T4.01

The 3 pandiagonal tori type T4.01 are here represented by the pandiagonal torus with index n° T4.01.1 (torus type n° T4.01.1). This pandiagonal torus displays 16 pandiagonal squares with Frénicle index n°s 102, 104, 174, 201, 279, 281, 365, 393, 473, 530, 565, 623, 690, 748, 785 and 828. All of these squares, (including the Frénicle index n°s 102 and 174 illustrated here), show complementary number patterns that are Dudeney type I.

Complementary number patterns of the semi-pandiagonal tori type T4.02.1

The 24 semi-pandiagonal tori type T4.02.1 are here represented by the semi-pandiagonal torus with index n° T4.115 (torus type n° T4.02.1.09). This semi-pandiagonal torus displays 8 semi-pandiagonal squares with Frénicle index n°s 48, 192, 255, 400, 570, 734, 763 and 824. Half of these squares, (including the Frénicle index n° 192 illustrated here), show complementary number patterns that are Dudeney type IV. The other half, (including the Frénicle index n° 48 illustrated here), show complementary number patterns that are Dudeney type VI.

Complementary number patterns of the semi-pandiagonal tori type T4.02.2

The 12 semi-pandiagonal tori type T4.02.2 are here represented by the semi-pandiagonal torus with index n° T4.059 (torus type n° T4.02.2.01). This semi-pandiagonal torus displays 8 semi-pandiagonal squares with Frénicle index n°s 21, 176, 213, 361, 445, 591, 808 and 860. Half of these squares, (including the Frénicle index n° 21 illustrated here), show complementary number patterns that are Dudeney type II. The other half, (including the Frénicle index n° 176 illustrated here), show complementary number patterns that are Dudeney type III.

Complementary number patterns of the semi-pandiagonal tori type T4.02.3

The 12 semi-pandiagonal tori type T4.02.3 are here represented by the semi-pandiagonal torus with index n° T4.085 (torus type n° T4.02.3.01). This semi-pandiagonal torus displays 8 semi-pandiagonal squares with Frénicle index n°s 32, 173, 228, 362, 425, 577, 798 and 853. All of these squares, (including the Frénicle index n°s 173 and 228 illustrated here), show complementary number patterns that are Dudeney type V.

Complementary number patterns of the partially pandiagonal tori type T4.03.1

The 6 partially pandiagonal tori type T4.03.1 are here represented by the partially pandiagonal torus with index n° T4.108 (torus type n° T4.03.1.1). This partially pandiagonal torus displays 4 partially pandiagonal squares with Frénicle index n°s 46, 50, 337 and 545. All of these squares, (including the Frénicle index n°s 46 and 545 illustrated here), show complementary number patterns that are Dudeney type VI.

As already mentioned in "A New Census of Fourth-Order Magic Squares," Dudeney overlooked the partially pandiagonal characteristics, and mistakenly classified these squares as "simple."

Complementary number patterns of the partially pandiagonal tori type T4.03.2

The 12 partially pandiagonal tori type T4.03.2 are here represented by the partially pandiagonal torus with index n° T4.195 (torus type n° T4.03.2.06). This partially pandiagonal torus displays 4 partially pandiagonal squares with Frénicle index n°s 208, 525, 526 and 693. Half of these squares, (including the Frénicle index n° 693 illustrated here), show complementary number patterns that are Dudeney type VII. The other half, (including the Frénicle index n° 208 illustrated here), show complementary number patterns that are Dudeney type IX.

As already mentioned in "A New Census of Fourth-Order Magic Squares," Dudeney overlooked the partially pandiagonal characteristics, and mistakenly classified these squares as "simple."

Complementary number patterns of the partially pandiagonal tori type T4.03.3

The 2 partially pandiagonal tori type T4.03.3 are here represented by the partially pandiagonal torus with index n° T4.217 (torus type n° T4.03.3.1). This partially pandiagonal torus displays 4 partially pandiagonal squares with Frénicle index n°s 181, 374, 484 and 643. All of these squares, (including the Frénicle index n°s 484 and 643 illustrated here), show complementary number patterns that are Dudeney type XI.

As already mentioned in "A New Census of Fourth-Order Magic Squares," Dudeney overlooked the partially pandiagonal characteristics, and mistakenly classified these squares as "simple."

Complementary number patterns of the partially pandiagonal tori type T4.04

The 4 partially pandiagonal tori type T4.04 are here represented by the partially pandiagonal torus with index n° T4.096 (torus type n° T4.04.1). This partially pandiagonal torus displays 2 partially pandiagonal squares with Frénicle index n°s 40 and 522. The square with Frénicle index n° 40 (illustrated here) shows a complementary number pattern that is Dudeney type VIII, whilst the other square with Frénicle index n° 522 (illustrated here) shows a complementary number pattern that is Dudeney type X.

As already mentioned in "A New Census of Fourth-Order Magic Squares," Dudeney overlooked the partially pandiagonal characteristics, and mistakenly classified these squares as "simple."

Complementary number patterns of the basic magic tori type T4.05.1

The 92 basic magic tori type T4.05.1 are here represented by the basic magic torus with index n° T4.002 (torus type n° T4.05.1.01). This basic magic torus displays 2 basic magic squares with Frénicle index n°s 1 and 458. Both of these squares, illustrated here, show complementary number patterns that are Dudeney type VI.

Complementary number patterns of the basic magic tori type T4.05.2

The 32 basic magic tori type T4.05.2 are here represented by the basic magic torus with index n° T4.049 (torus type n° T4.05.2.01). This basic magic torus displays 2 basic magic squares with Frénicle index n°s 23 and 767. The square with Frénicle index n° 767 (illustrated here) shows a complementary number pattern that is Dudeney type VII, whilst the square with Frénicle index n° 23 (illustrated here) shows a complementary number pattern that is Dudeney type IX.

Complementary number patterns of the basic magic tori type T4.05.3

The 4 basic magic tori type T4.05.3 are here represented by the basic magic torus with index n° T4.005 (torus type n° T4.05.3.1). This basic magic torus displays 2 basic magic squares with Frénicle index n°s 3 and 613. Both of these squares, illustrated here, show complementary number patterns that are Dudeney type XII.

Complementary number patterns of the basic magic tori type T4.05.4

The 52 basic magic tori type T4.05.4 are here represented by the basic magic torus with index n° T4.019 (torus type n° T4.05.4.1). This basic magic torus displays 2 basic magic squares with Frénicle index n°s 8 and 343. The square with Frénicle index n° 8 (illustrated here) shows a complementary number pattern that is Dudeney type VIII, whilst the square with Frénicle index n° 343 (illustrated here) shows a complementary number pattern that is Dudeney type X.

Conclusions

We can see that the Dudeney pattern types I, V, XI, and XII are not only valid for magic squares, but also for the magic tori that display these squares. On the other hand, the Dudeney pattern types II and III are shown to be partial viewpoints of a single pattern on the fourth-order magic tori. Again, the Dudeney pattern types IV and VI, the Dudeney pattern types VII and IX, and also the Dudeney pattern types VIII and X, are shown to be partial viewpoints of single patterns on the fourth-order magic tori.

We also notice that some of the detected complementary number patterns have contrasting hemitorus arrangements.

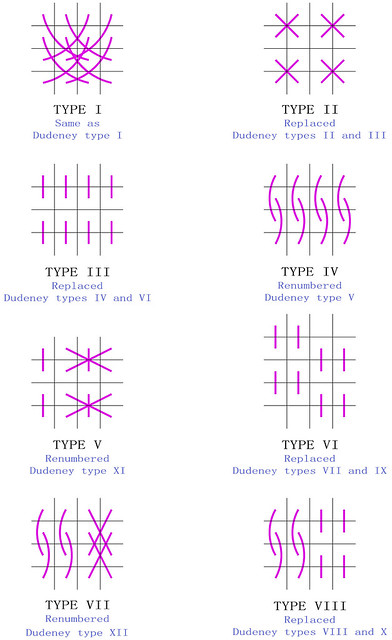
It is necessary to adapt the Dudeney pattern types, and add new symbols that not only reveal the real nature of the complementary number relationships, but also facilitate their comprehension. With this in mind, the 8 figures that follow have been selected to illustrate the essentially different complementary number pattern types that occur on fourth-order magic tori:

To be read with a previous table that compared the 12 Dudeney pattern types with the 12 Magic torus types, published in "A New Census of Fourth-Order Magic Squares," the new table that follows, recapitulates the latest findings, and shows the repartition of the 8 complementary number patterns on the magic squares of the fourth-order magic tori:

Further Developments

New articles entitled "Self-Complementary and Paired Complementary Magic Tori of Order-4" and "Multiplicative Magic Tori" now extend the above findings.

Read more ...

Magic Sequences of the Sub-Magic 2x2 Squares of 4th-Order Magic Tori

The number of fourth-order magic series is 86. The complete list of these magic series has been published by Walter Trump, who gave me confirmation that all of these magic series were present on fourth-order magic squares, even if the geometrical arrangement of the series was often chaotic. He pointed out that for example the series 7+8+9+10 does not exist in any row, column, or main diagonal of a magic 4x4-square, even when considering all the 24 possible permutations of the four numbers. However the series 7+8+9+10 occurs in the 2x2 centre square or in the four corners of certain 4x4 magic squares. As defined in MathWorld, or in Wikipedia, a magic series is not a specific sequence of numbers, but a set of numbers that add up to the magic constant.

The magic constant (MCn) of an nth order magic square (or torus) can be calculated:

MCn = (n²)² + n²  x  1    =    n(n² + 1)

                 2             n                2

For a fourth-order magic square (or magic torus) the magic constant is therefore:
MC4   =  4(4² + 1)    =   34
                     2

Magic sequences of the sub-magic 2x2 squares on fourth-order magic tori

On any sub-magic 2x2 square of a fourth-order magic torus (or of an order 4 magic square) :

a + b + c + d = 34

Considering a clockwise arrangement of the numbers on the sub-magic 2x2 square, each of the 86 4th-order magic series can be expressed in 3 essentially different sequences:

 

Clockwise and anti-clockwise sequences are considered equivalent, depending on whether the magic torus is being contemplated from the outside or from within. The magic torus concept is explained in a previous article "From the Magic Square to the Magic Torus." The interrelationships of the 4th-order magic tori, first explored in the "Fourth-Order Magic Torus Chart," are now more extensively detailed in "Multiplicative Magic Tori."

Theoretically the total number of different sub-magic 2x2 squares on fourth-order magic tori would be 86 magic series x 3 sequence types = 258. However, after checking the 255 different fourth-order magic tori I discovered that there are 134 exceptions, leaving only 124 essentially different sub-magic 2x2 square sequences. These exceptions are of course the result of combination impossibilities that can be tested and eliminated by computer calculation. However, as I do not use computer programming myself, I wondered if it might be possible to find simpler ways of distinguishing the magic sequences from their non-magic counterparts. My observations have enabled me to determine some of the rules that govern fourth-order sub-magic 2x2 square sequences:

Rules for sub-magic 2x2 square sequences on fourth-order magic tori:

Rule 1: The magic series a + b + c + d (whatever the order of the sequence) must always contain two

even  numbers and two odd numbers.

Rule 2: The numbers of the magic series must always be balanced this way:
             1 ≤ a ≤ 7
             2 ≤ b ≤ 8
             9 ≤ c ≤ 15
           10 ≤ d ≤ 16

Rule 3: If there is a single occurrence of consecutive numbers where the successor number is even, then none of the sequences of the series will be magic.

         

Rule 4: If the series contains complementary numbers a + d = 17 and b + c = 17, and if there is a double occurrence of consecutive numbers where the successor number is even, only the sequences that restrict these successive numbers to the diagonals of the sub-magic 2x2 square will be magic. Some of the odd - even - odd - even series of complementary pairs have this characteristic and the only magic sequences of these series are therefore type C.

 
Rule 5: If the series contains complementary numbers a + d = 17 and b + c = 17,
             and if a - 1 = 8 - b = c - 9 = 16 - d
             implying that (c + d) - (a + b) = n²
             then only the sequence type A will be magic.
             (as this only occurs with odd-even-odd-even, and even-odd-even-odd series).

Rule 6: If the series contains complementary numbers a + d = 17 and b + c = 17,
             and if the series is odd - odd - even - even,
             and if (c + d) - (a + b) is not a multiple of 3,  
             then only the sequence C (odd - even - odd - even) will be magic.

Rule 7: If the series contains complementary numbers a + d = 17 and b + c = 17,
             and if the series is even - even - odd - odd,
             and if (c + d) - (a + b) is not a multiple of 7,  
             then only the sequence C (even - odd - even - odd) will be magic.

Presentation of the list of magic sequences

In the list that follows the index numbers of the magic series are the same as those already published by Walter Trump. I have just added the suffixes A, B, and C to identify the 3 essentially different sequences that are derived from each series. I wish to emphasise that although I have always chosen the lowest number to be the first, none of the sequences have either a beginning or an end, as they each form a continuous circuit within their sub-magic 2x2 square.

It was difficult to decide how to present the results. I have chosen to list the different sequence types A, B, and C separately, and I have grouped the sequences by sets of number rhythms in order to facilitate comparisons and reveal patterns. I have also sorted between the complementary (a+d = b+c = n²+1) sequences and the non-complementary (a+d ≠ b+c) sequences.

Please note that if you click on the button that appears at the top right hand side of the pdf viewer below, a new window will open and full size pages of the paper will then be displayed, with options for zooming.

Observations

The complementary series (a + d = c + b = n² + 1) have, where possible, been divided into pairs of sequences that share similar characteristics. Although the sub-magic 2x2 square magic series 1 + 2 + 15 + 16, and 3 + 4 + 13 + 14 seem similar, I have preferred to stick to the same sets already used in my study of the orthogonal sequences. These include 4 exceptions with unique characteristics that cannot be easily paired:

1 + 2 + 15 + 16
3 + 4 + 13 + 14
5 + 6 + 11 + 12
7 + 8 +  9  + 10

There are many other ways of ordering the sequences to accord with the specific number rhythms of the different magic torus types. This is why an ideal list, that will suit all the torus types, remains a difficult objective.

Read more ...