Complementary Number Patterns on Fourth-Order Magic Tori

The 880 fourth-order magic squares were first identified and listed by Bernard Frénicle de Bessy in his « Table générale des quarrez magiques de quatre, » which was published posthumously in 1693, in his book « Des quarrez magiques. » The census of these 880 4x4 squares is given in the appendix to the book « New Recreations With Magic Squares » by William H. Benson and Oswald Jacoby (Edition 1976), and also on the website of the late Harvey D. Heinz:  Frénicle n° 1 à 200, Frénicle n° 201 à 400, Frénicle n° 401 à 600, Frénicle n° 601 à 880.

Further to Bernard Frénicle de Bessy's initial findings, Henry Ernest Dudeney then classified the 880 fourth-order magic squares under 12 pattern types, in "The Queen" in 1910, (later republished in his book  "Amusements in Mathematics" in 1917). These patterns were determined through the observation of the relative positions of complementary pairs of numbers (which add up to N²+1 when N is the order of the square).

Although the different Dudeney pattern types can indeed be observed on fourth-order magic squares, they cannot be used for the classification of the fourth-order magic tori that display these squares. A Dudeney pattern type can be misleading because it depends on a bordered magic square viewpoint, whilst the magic torus that displays the magic square has a limitless surface...

In the study that follows the complementary number patterns are therefore tested, by comparing a developed torus surface and two traditional Frénicle magic square viewpoints for each of the 12 different types of fourth-order magic tori.

Complementary number patterns of each fourth-order magic torus type

General information on the magic torus index and type numbers

In addition to the Frénicle index numbers and the Dudeney types that have already been mentioned above, the present study also uses the index and type numbers of the fourth-order magic tori. For readers who may not be acquainted with the subject, essential information can be found in the following pages:

In a previous article "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus," the fourth-order magic tori have been classed in 12 types, and each magic torus has received a specific type number.

In a previous article "Table of Fourth-Order Magic Tori," so as to facilitate the identification of a magic torus beginning with any magic square, a standard torus form has also been defined, and each of the 255 fourth-order magic tori has received a specific index number.

Complementary number patterns of the pandiagonal tori type T4.01

The 3 pandiagonal tori type T4.01 are here represented by the pandiagonal torus with index n° T4.01.1 (torus type n° T4.01.1). This pandiagonal torus displays 16 pandiagonal squares with Frénicle index n°s 102, 104, 174, 201, 279, 281, 365, 393, 473, 530, 565, 623, 690, 748, 785 and 828. All of these squares, (including the Frénicle index n°s 102 and 174 illustrated here), show complementary number patterns that are Dudeney type I.

Complementary number patterns of the semi-pandiagonal tori type T4.02.1

The 24 semi-pandiagonal tori type T4.02.1 are here represented by the semi-pandiagonal torus with index n° T4.115 (torus type n° T4.02.1.09). This semi-pandiagonal torus displays 8 semi-pandiagonal squares with Frénicle index n°s 48, 192, 255, 400, 570, 734, 763 and 824. Half of these squares, (including the Frénicle index n° 192 illustrated here), show complementary number patterns that are Dudeney type IV. The other half, (including the Frénicle index n° 48 illustrated here), show complementary number patterns that are Dudeney type VI.

Complementary number patterns of the semi-pandiagonal tori type T4.02.2

The 12 semi-pandiagonal tori type T4.02.2 are here represented by the semi-pandiagonal torus with index n° T4.059 (torus type n° T4.02.2.01). This semi-pandiagonal torus displays 8 semi-pandiagonal squares with Frénicle index n°s 21, 176, 213, 361, 445, 591, 808 and 860. Half of these squares, (including the Frénicle index n° 21 illustrated here), show complementary number patterns that are Dudeney type II. The other half, (including the Frénicle index n° 176 illustrated here), show complementary number patterns that are Dudeney type III.

Complementary number patterns of the semi-pandiagonal tori type T4.02.3

The 12 semi-pandiagonal tori type T4.02.3 are here represented by the semi-pandiagonal torus with index n° T4.085 (torus type n° T4.02.3.01). This semi-pandiagonal torus displays 8 semi-pandiagonal squares with Frénicle index n°s 32, 173, 228, 362, 425, 577, 798 and 853. All of these squares, (including the Frénicle index n°s 173 and 228 illustrated here), show complementary number patterns that are Dudeney type V.

Complementary number patterns of the partially pandiagonal tori type T4.03.1

The 6 partially pandiagonal tori type T4.03.1 are here represented by the partially pandiagonal torus with index n° T4.108 (torus type n° T4.03.1.1). This partially pandiagonal torus displays 4 partially pandiagonal squares with Frénicle index n°s 46, 50, 337 and 545. All of these squares, (including the Frénicle index n°s 46 and 545 illustrated here), show complementary number patterns that are Dudeney type VI.

As already mentioned in "A New Census of Fourth-Order Magic Squares," Dudeney overlooked the partially pandiagonal characteristics, and mistakenly classified these squares as "simple."

Complementary number patterns of the partially pandiagonal tori type T4.03.2

The 12 partially pandiagonal tori type T4.03.2 are here represented by the partially pandiagonal torus with index n° T4.195 (torus type n° T4.03.2.06). This partially pandiagonal torus displays 4 partially pandiagonal squares with Frénicle index n°s 208, 525, 526 and 693. Half of these squares, (including the Frénicle index n° 693 illustrated here), show complementary number patterns that are Dudeney type VII. The other half, (including the Frénicle index n° 208 illustrated here), show complementary number patterns that are Dudeney type IX.

As already mentioned in "A New Census of Fourth-Order Magic Squares," Dudeney overlooked the partially pandiagonal characteristics, and mistakenly classified these squares as "simple."

Complementary number patterns of the partially pandiagonal tori type T4.03.3

The 2 partially pandiagonal tori type T4.03.3 are here represented by the partially pandiagonal torus with index n° T4.217 (torus type n° T4.03.3.1). This partially pandiagonal torus displays 4 partially pandiagonal squares with Frénicle index n°s 181, 374, 484 and 643. All of these squares, (including the Frénicle index n°s 484 and 643 illustrated here), show complementary number patterns that are Dudeney type XI.

As already mentioned in "A New Census of Fourth-Order Magic Squares," Dudeney overlooked the partially pandiagonal characteristics, and mistakenly classified these squares as "simple."

Complementary number patterns of the partially pandiagonal tori type T4.04

The 4 partially pandiagonal tori type T4.04 are here represented by the partially pandiagonal torus with index n° T4.096 (torus type n° T4.04.1). This partially pandiagonal torus displays 2 partially pandiagonal squares with Frénicle index n°s 40 and 522. The square with Frénicle index n° 40 (illustrated here) shows a complementary number pattern that is Dudeney type VIII, whilst the other square with Frénicle index n° 522 (illustrated here) shows a complementary number pattern that is Dudeney type X.

As already mentioned in "A New Census of Fourth-Order Magic Squares," Dudeney overlooked the partially pandiagonal characteristics, and mistakenly classified these squares as "simple."

Complementary number patterns of the basic magic tori type T4.05.1

The 92 basic magic tori type T4.05.1 are here represented by the basic magic torus with index n° T4.002 (torus type n° T4.05.1.01). This basic magic torus displays 2 basic magic squares with Frénicle index n°s 1 and 458. Both of these squares, illustrated here, show complementary number patterns that are Dudeney type VI.

Complementary number patterns of the basic magic tori type T4.05.2

The 32 basic magic tori type T4.05.2 are here represented by the basic magic torus with index n° T4.049 (torus type n° T4.05.2.01). This basic magic torus displays 2 basic magic squares with Frénicle index n°s 23 and 767. The square with Frénicle index n° 767 (illustrated here) shows a complementary number pattern that is Dudeney type VII, whilst the square with Frénicle index n° 23 (illustrated here) shows a complementary number pattern that is Dudeney type IX.

Complementary number patterns of the basic magic tori type T4.05.3

The 4 basic magic tori type T4.05.3 are here represented by the basic magic torus with index n° T4.005 (torus type n° T4.05.3.1). This basic magic torus displays 2 basic magic squares with Frénicle index n°s 3 and 613. Both of these squares, illustrated here, show complementary number patterns that are Dudeney type XII.

Complementary number patterns of the basic magic tori type T4.05.4

The 52 basic magic tori type T4.05.4 are here represented by the basic magic torus with index n° T4.019 (torus type n° T4.05.4.1). This basic magic torus displays 2 basic magic squares with Frénicle index n°s 8 and 343. The square with Frénicle index n° 8 (illustrated here) shows a complementary number pattern that is Dudeney type VIII, whilst the square with Frénicle index n° 343 (illustrated here) shows a complementary number pattern that is Dudeney type X.

Conclusions

We can see that the Dudeney pattern types I, V, XI, and XII are not only valid for magic squares, but also for the magic tori that display these squares. On the other hand, the Dudeney pattern types II and III are shown to be partial viewpoints of a single pattern on the fourth-order magic tori. Again, the Dudeney pattern types IV and VI, the Dudeney pattern types VII and IX, and also the Dudeney pattern types VIII and X, are shown to be partial viewpoints of single patterns on the fourth-order magic tori.

We also notice that some of the detected complementary number patterns have contrasting hemitorus arrangements.

It is necessary to adapt the Dudeney pattern types, and add new symbols that not only reveal the real nature of the complementary number relationships, but also facilitate their comprehension. With this in mind, the 8 figures that follow have been selected to illustrate the essentially different complementary number pattern types that occur on fourth-order magic tori:

To be read with a previous table that compared the 12 Dudeney pattern types with the 12 Magic torus types, published in "A New Census of Fourth-Order Magic Squares," the new table that follows, recapitulates the latest findings, and shows the repartition of the 8 complementary number patterns on the magic squares of the fourth-order magic tori:

Further Developments

New articles entitled "Self-Complementary and Paired Complementary Magic Tori of Order-4" and "Multiplicative Magic Tori" now extend the above findings.

Read more ...

A New Census of Fourth-Order Magic Squares

Since Mr Henry Ernest Dudeney's first article in "The Queen" on the 15th January 1910, (the findings of which he confirmed on the page 120 of his book "Amusements in Mathematics", in 1917), the present generally accepted census of fourth-order magic squares includes three main categories as follows:

"Nasik" (Pandiagonal) : 48 magic squares

"Semi-Nasik" (Semi-pandiagonal) : 384 magic squares

"Simple" (Basic magic) : 448 magic squares

All Types : 880 = the total number of essentially different 4th-order magic squares in Frénicle standard form.

After defining magic squares as: "in their simple form of consecutive whole numbers arranged in a square so that every column, every row, and each of the two long diagonals shall add up alike," Dudeney then characterised his three main categories of fourth-order magic squares as follows:

A "Simple" square is a "square that fulfils the simple conditions and no more."
A "Semi-Nasik" (or semi-pandiagonal) square "has the additional property that the opposite short diagonals of two cells each together sum to 34."
A "Nasik" (or pandiagonal) square is a magic square on which "all the broken diagonals sum to 34."

This census was misleading, as Dudeney implied that for all his "simple" magic squares, only the main diagonals were magic. Because this was not the case, he had erroneously categorised certain partially pandiagonal squares as "simple" magic squares: There are 88 fourth-order partially pandiagonal squares that have been neglected until now, perhaps because their magic diagonals are only singly symmetric and did not satisfy Dudeney's initial conditions for semi-pandiagonal classification...

Considering the commencement of pandiagonality to take place when at least one of a magic square's broken diagonals is magic, and wishing to clarify the classification of these squares, I propose that 88 partially pandiagonal squares (including six Dudeney types VI, VII, VIII, IX, X, and XI) should be taken into account. These squares are identified in a previous article: "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus." For example the Frénicle index squares n° 46, 50, 337 and 545, classed "simple" by Dudeney, all share the same partially pandiagonal characteristics, displayed on the magic torus T4.108 (type n° T4.03.1.1). It is clear that these partially pandiagonal squares, with two singly symmetric broken diagonals, are essentially different when compared with their basic, or "simple," fourth-order magic square cousins:

Additionally, the Frénicle index squares n° 40 and 552, classed "simple" by Dudeney, both share the same partially pandiagonal characteristics, displayed on the magic torus T4.096 (type n° T4.04.01). It is clear that these partially pandiagonal squares, with one singly symmetric broken diagonal, are essentially different when compared with their basic, or "simple," fourth-order magic square cousins:

Since highlighting the 255 magic tori that display the 880 Frénicle magic squares, I now propose five main categories of 4th-order magic squares as follows:

Pandiagonal ("Nasik") : 48 magic squares
Semi-pandiagonal ("Semi-Nasik") : 384 magic squares with 2 four times symmetric broken magic diagonals
Partially pandiagonal : 80 magic squares with 2 singly symmetric broken magic diagonals
Partially pandiagonal : 8 magic squares with 1 singly symmetric broken magic diagonal
Basic ("Simple") : 360 magic squares
All Types : 880 = the total number of essentially different 4th-order magic squares in Frénicle standard form.

Nevertheless, these 4th-order magic squares only offer partial glimpses of the convex or concave 2D number systems that they represent. Instead of counting the magic squares we could be reasoning otherwise, and I therefore also propose an alternative census of the 255 essentially different magic tori that display the 880 4th-order magic squares:

Pandiagional : 3 Tori Type 4.01 with 8 crossed magic diagonals producing 16 magic intersections. Each torus T4.01 is entirely covered by 16 sub-magic 2x2 squares.
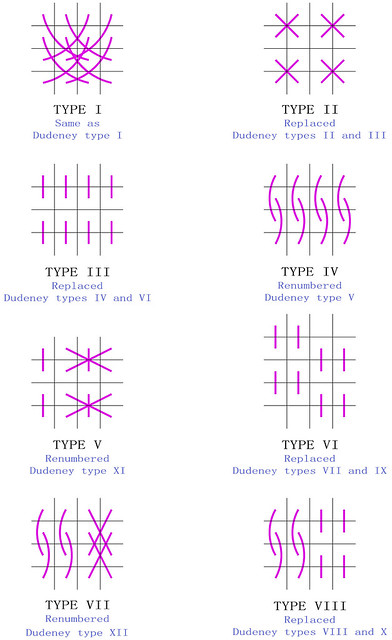
The 48 pandiagonal squares that are displayed are Dudeney type I.
Semi-pandiagonal : 24 Tori Type 4.02.1 with 4 crossed magic diagonals producing 8 magic intersections. Each torus T4.02.1 is entirely covered by 12 sub-magic 2x2 squares.
The 192 semi-pandiagonal squares that are displayed are Dudeney types IV and VI
Semi-pandiagonal : 12 Tori Type 4.02.2 with 4 crossed magic diagonals producing 8 magic intersections. Each torus T4.2.2 is entirely covered by 8 sub-magic 2x2 squares.
The 96 semi-pandiagonal squares that are displayed are Dudeney type II and III.
Semi-pandiagonal : 12 Tori Type 4.02.3 with 4 crossed magic diagonals producing 8 magic intersections. Each torus T4.02.3 is entirely covered by 8 sub-magic 2x2 squares.
The 96 semi-pandiagonal squares that are displayed are Dudeney type V.
Partially pandiagonal : 6 Tori Type 4.03.1 with 4 crossed magic diagonals producing 4 magic intersections. Each torus T4.03.1 is entirely covered by 8 sub-magic 2x2 squares.
The 24 partially panpandiagonal squares that are displayed are Dudeney type VI.
Partially pandiagonal : 12 Tori Type 4.03.2 with 4 crossed magic diagonals producing 4 magic intersections. Each torus T4.03.2 is entirely covered by 8 sub-magic 2x2 squares.
The 48 partially pandiagonal squares that are displayed are Dudeney types VII and IX.
Partially pandiagonal : 2 Tori Type 4.03.3 with 4 crossed magic diagonals producing 4 magic intersections. Each torus T4.03.3 is entirely covered by 8 sub-magic 2x2 squares.
The 8 partially pandiagonal squares that are displayed are Dudeney type XI.
Partially pandiagonal : 4 Tori Type 4.04 with 3 crossed magic diagonals producing 2 magic intersection. Each torus T4.04 is entirely covered by 4 sub-magic 2x2 squares.
The 8 partially pandiagonal squares that are displayed are Dudeney types VIII and X.
Basic : 92 Tori Type 4.05.1 with 2 crossed magic diagonals producing 2 magic intersections. Each torus T4.05.1 is entirely covered by 8 sub-magic 2x2 squares.
The 184 basic magic squares that are displayed are Dudeney type VI.
Basic : 32 Tori Type 4.05.2 with 2 crossed magic diagonals producing 2 magic intersections. Each torus T4.05.2 is entirely covered by 8 sub-magic 2x2 squares.
The 64 basic magic squares that are displayed are Dudeney types VII and IX.
Basic : 4 Tori Type 4.05.3 with 2 crossed magic diagonals producing 2 magic intersections. Each torus T4.05.3 is entirely covered by 4 sub-magic 2x2 squares.
The 8 basic magic squares that are displayed are Dudeney type XII.
Basic : 52 Tori Type 4.05.4 with 2 crossed magic diagonals producing 2 magic intersections. Each torus T4.05.4 is entirely covered by 4 sub-magic 2x2 squares.
The 104 basic magic squares that are displayed are Dudeney types VIII and X.
All Types : 255 = the total number of essentially different fourth-order magic tori.

The first table below compares the magic square enumerations using the 12 Dudeney types and the 12 Magic torus types. If you click on this table, a full-size version will open in a new window, which will allow for easier reading:

The second table below recapitulates the different characteristics of the 255 fourth-order magic tori and the magic squares that they display:

For convenient reference, the 255 magic tori that display the 880 fourth-order magic squares are now indexed and listed in normalised square form, in the "Table of Fourth-Order Magic Tori."

For further analysis of this new fourth-order magic square census, please refer to Dwane Campbell's web site, in which he has made interesting studies of 4th-order Frénicle squares constructed from base squares, and also a comparison of the Dudeney and Walkington classifications.

I wish to express my gratitude to Walter Trump, not only for his valuable advice concerning the choice of terminology, but also for his computing skills that identified the fourth-order magic torus type 4.04, and enabled a precise count.

My thanks also go out to Miguel Angel Amela who ran a computer program that confirmed the different counts of magic diagonals on 4th-order magic squares.

I also wish to express my thanks to Harry White who kindly ran a program to check and validate my hypothesis that sub-magic 2x2 squares entirely cover each 4th-order magic torus.

New development!

Posted on the 24th April 2024, an article entitled "Plus or Minus Groups of Magic Tori of Order 4" shows The minimum number of ± groups that display all of the 255 Magic Tori of order 4 is 137, a Pythagorean prime of the form 4 k + 1, where k = 34, and 137 = 4 × 34 + 1. Though it may just be pure coincidence, we cannot help noticing that: not only 4 is the dimension of the order in question, but also that 34 is its magic sum!

Read more ...