Sub-Magic 2x2 Squares on Fourth-Order Magic Tori

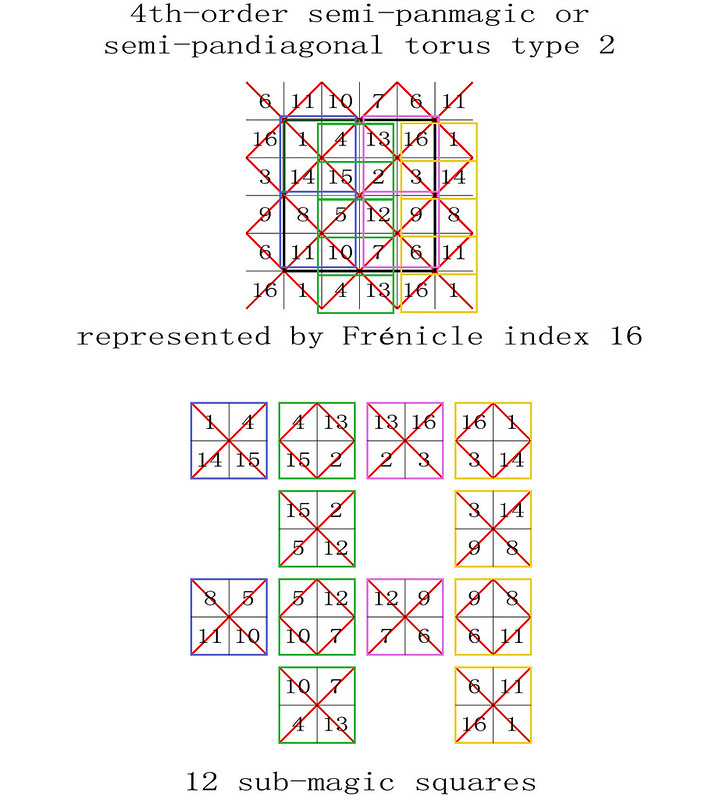
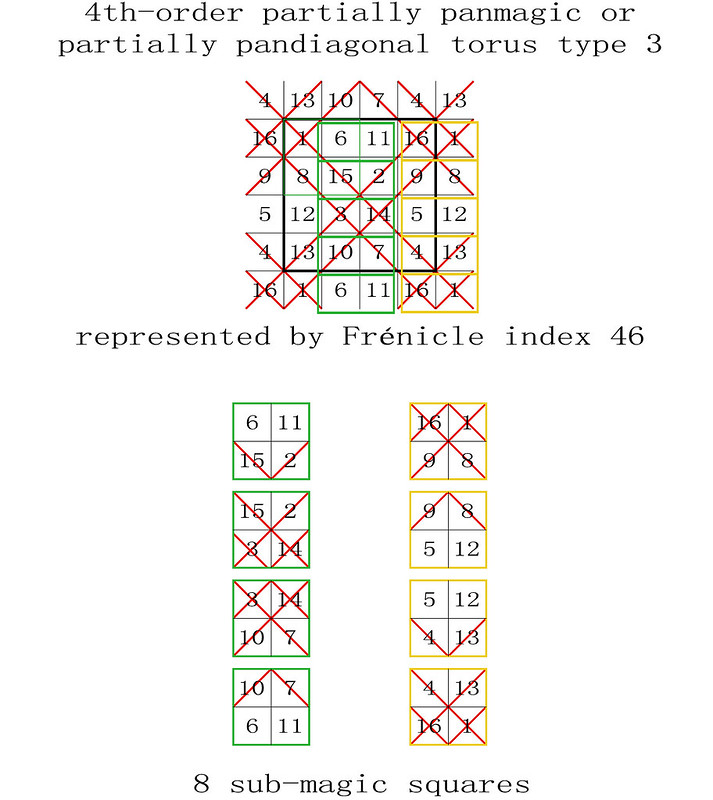
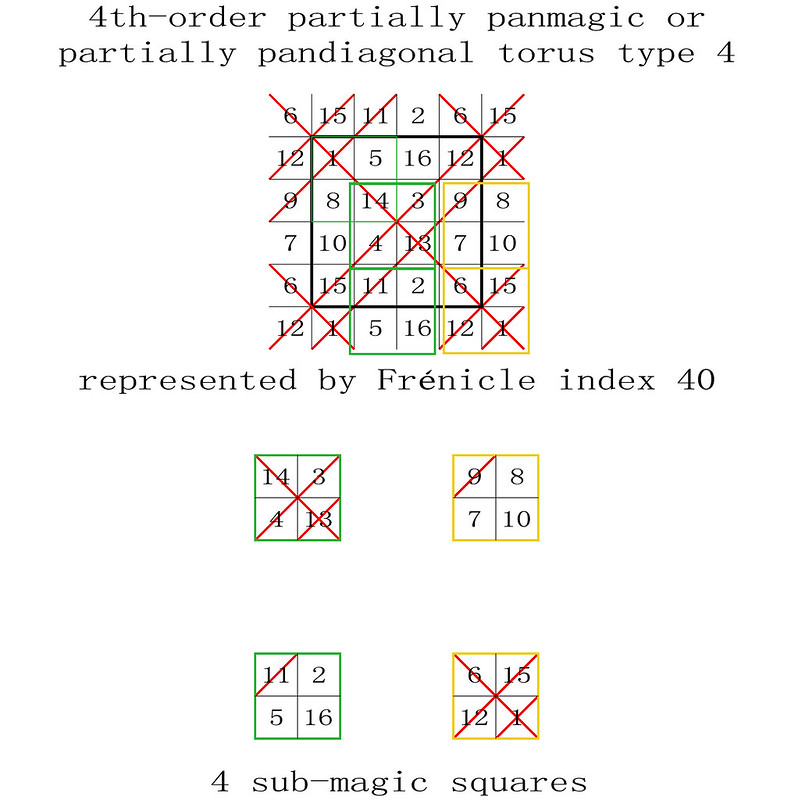
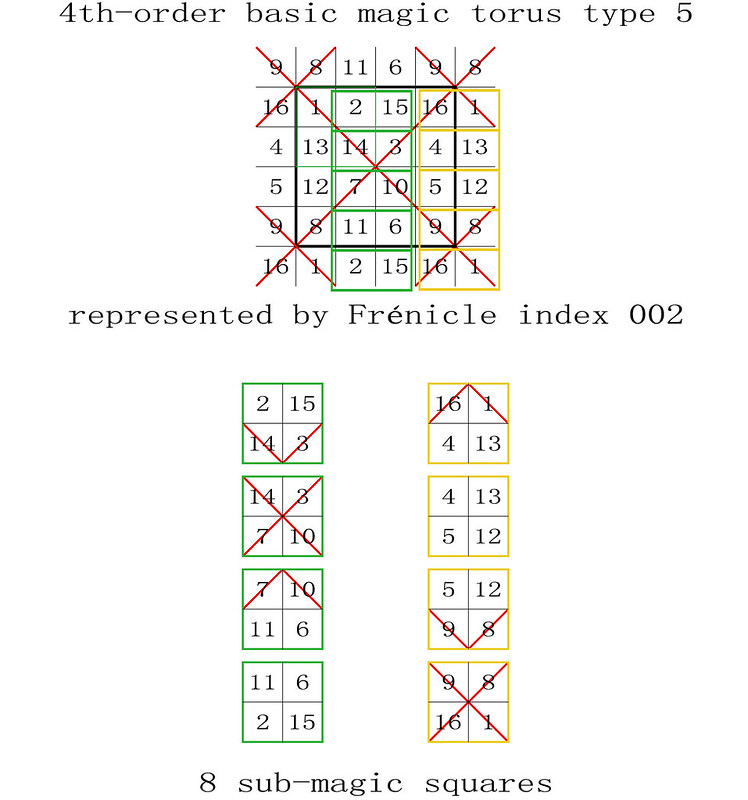
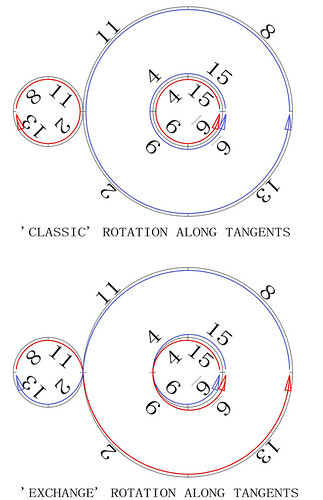
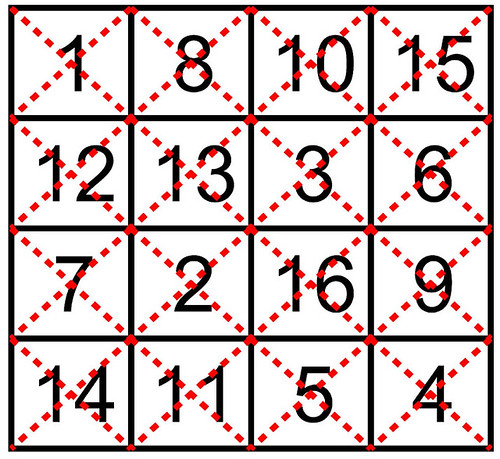
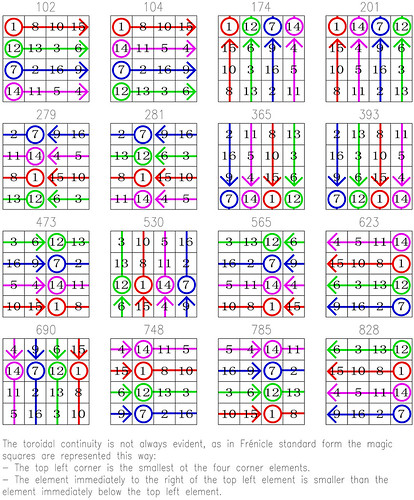
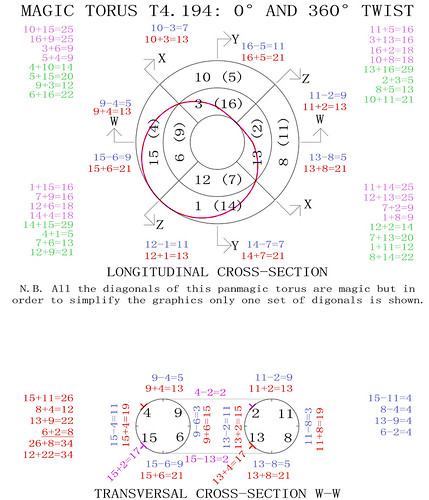
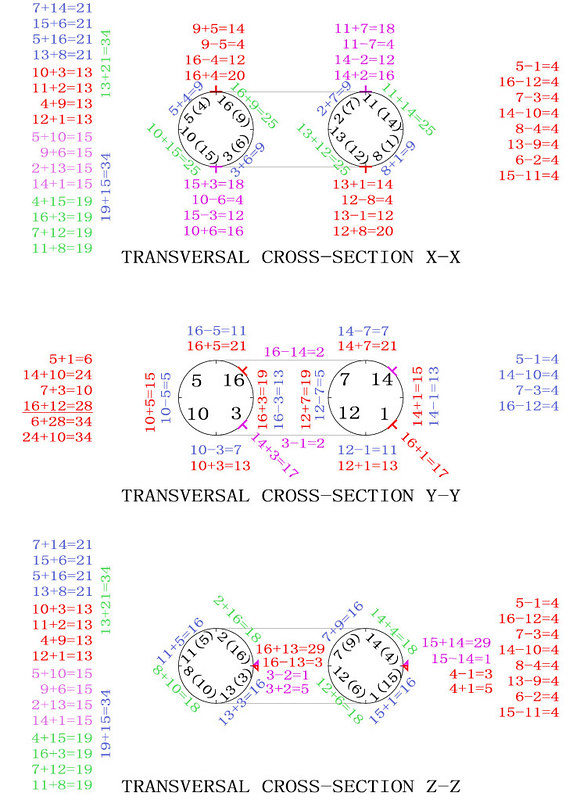
My recent studies have shown that 2x2 sub-magic squares are fundamental in the way the fourth-order magic tori work.

It has long been known that fourth-order magic squares have 2x2 sub-magic squares at their centres and that the 4 corner numbers of the squares also add up to 34. However, once considered as magic tori, the 4 corner numbers of each 4th-order magic square are in fact another sub-magic 2x2 square, and more subsquares are to be found overlapping the former boundary of the initial square.

I have therefore tried to determine the number of magic sub-magic squares that are displayed on each type of the fourth-order magic tori, and my first results are illustrated below. Using simple observation and manual input I have not verified all of the 880 Frénicle fourth-order squares and may have missed something. Your comments and corrections are welcome.

Surprisingly the fourth-order type 4 partially panmagic torus displays less sub-magic 2x2 squares than the basic fourth-order type 5 magic torus.

Hypothesis

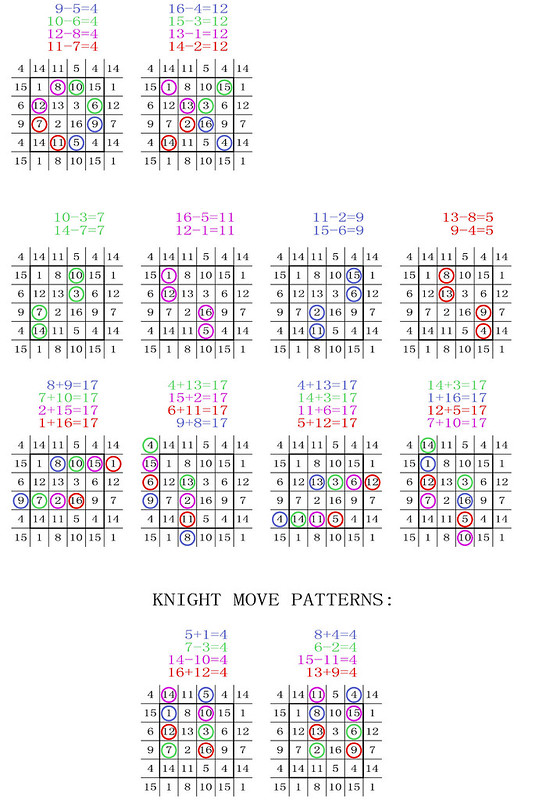
Each number of a fourth-order magic torus (or magic square) comes from at least one 2x2 sub-magic square. Or, expressed otherwise, the surface of every fourth-order magic torus is entirely covered by 2x2 sub-magic squares.

Conclusion

The above remained to be verified by a computer programme until the day after this article was published when Harry White very kindly checked and validated the hypothesis: His results confirm that every 4th-order magic torus (or magic square) is entirely covered by 2x2 sub-magic squares. For all the 880 Frénicle squares he has found 7,712 sub-squares and has confirmed that all the numbers of the different magic squares come from at least one 2x2 sub-magic square.

Harry White's results show that within a same type of tori the patterns and numbers of sub-squares can vary. For example, some of the type 5 tori have a reduced cover of 4 sub-magic squares instead of the 8 subsquares shown above (for example the Frénicle square index 277). This will need to be investigated further.

Please note that I have just published (the 28th March 2013) a new article that takes into account the different arrangements of the sub-magic 2x2 squares, and which attempts to complete the picture.

As for 4th-order semi-magic squares I have started to look into the question and have discovered some examples which are totally covered by 4 2x2 sub-magic squares whilst other examples have no subsquares at all: The phenomenon is not just limited to the magic tori.

Read more ...

Fourth-Order Panmagic Torus T4.194

The illustration shows the interchangeability of horizontal or vertical representations of a same panmagic torus. By twisting one side of the interlocked torus the other side turns, and vice versa. A simultaneous twisting and turning movement is also possible. The contact between the two sides of the interlocked torus takes place along perpendicularly connected circular tangents.

Interlocked Pandiagonal Torus - (excluded from CC licence)

 What happens at the intersection of these tangents? Here are two ways of seeing things:

The interlocked magic torus could symbolise the interaction between opposites such as behind and in front, outside and inside, etc. Alternatively, if one side of the torus represents the past and the other the future, the present could take place along the two perpendicular circular tangents.

Leaving philosophical considerations, and returning to mathematics, the above illustration portrays a pandiagonal or panmagic torus classified by type n°T4.01.1 - see the previous article "255 Fourth-Order Magic Tori, and 1 Third-Order Magic Torus" The torus displays 16 fourth-order pandiagonal squares (Frénicle index numbers 102, 104, 174, 201, 279, 281, 365, 393, 473, 530, 565, 623, 690, 748, 785, and 828). Since the publication of a new "Table of Fourth-Order Magic Tori" this torus is now also indexed and listed as the n° T4.194 in normalised square form:

Numbered following the Bernard Frénicle de Bessy index, the pandiagonal squares that are displayed on this pandiagonal torus are as follows:  

The illustration below shows a way to spot the similar number sequences in the different Frénicle squares showing that they come from the same magic torus:

In order to better visualise how the T4.194 torus works I have produced the diagrams below. The magic torus is a symmetrically stable number system. When the torus is twisted through 360° changing number couples produce continuously balanced tensions. I have indicated some of the mathematical properties but you will notice others when you contemplate this beautiful counting machine. Further below, the results of the study are illustrated by patterns on the panmagic square.

Read more ...